高考数学一轮复习考点测试刷题本26 平面向量的概念及线性运算（含答案解析）

2020高考数学(文数)考点测试刷题本26

平面向量的概念及线性运算

一         、选择题

1.已知向量a，b是两个不共线的向量，若向量m=4a＋b与n=a－λb共线，则实数λ的值为(　　)

A．－4          B．－            C．            D．4

2.已知a，b是不共线的向量，=λa＋b，=a＋μb，λ，μ∈R，则A，B，C三点共线的充要条件为(　　)

A．λ＋μ=2           B．λ－μ=1        C．λμ=－1          D．λμ=1

3.已知点M是△ABC的边BC的中点，点E在边AC上，且=2，则=(　　)

A．＋        B．＋       C．＋        D．＋

4.设D为△ABC所在平面内一点，=3，则(　　)

A．=－＋      B．=－       C．=＋        D．=－

5.在△ABC中，AD为BC边上的中线，E为AD的中点，则=(　　)

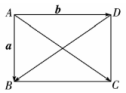
A．－          B．－        C．＋          D．＋

6.如图，在△ABC中，已知D为边BC的中点，E，F，G依次为线段AD从上至下的3个四等分点，若＋=4，则(　　)

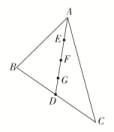
A．点P与图中的点D重合        B．点P与图中的点E重合

C．点P与图中的点F重合        D．点P与图中的点G重合

7.如图，在直角梯形ABCD中，AB=2AD=2DC，E为BC边上一点，=3E，F为AE的中点，则=(　　)

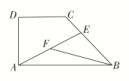
A．－         B．－        C．－＋        D．－＋

8.如图，在△ABC中，=，P是BN上的一点，若=m＋，则实数m的值为(　　)

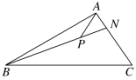
A.               B.            C．1              D．3

二         、填空题

9.设点P是△ABC所在平面内一点，且＋=2，则＋=________．

10.在△ABC中，点M，N满足=2，=．若=x＋y，则x=______；y=______．

11.平行四边形ABCD中，M为BC的中点，若=λ＋μ，则λμ=________.

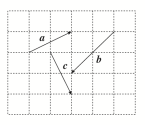
12.在如图所示的方格纸中，向量a，b，c的起点和终点均在格点(小正方形顶点)上，若c与xa＋yb(x，y为非零实数)共线，则的值为________．

三         、解答题

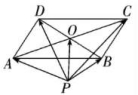
13.如图,平行四边形ABCD中，对角线AC与BD交于点O，P为平面内任意一点.

求证：＋＋＋=4.

14.已知|a|=6，|b|=8，且|a＋b|=|a－b|，求|a－b|.

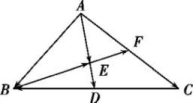
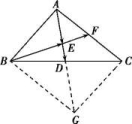
15.如图所示,在△ABC中,D,F分别是BC,AC的中点,=,=a,=b.

(1)用a,b表示向量,,,,;

(2)求证:B,E,F三点共线.

16.已知O，A，B是不共线的三点，且=m＋n (m，n∈R)．

(1)若m＋n=1，求证：A，P，B三点共线；

(2)若A，P，B三点共线，求证：m＋n=1.

答案解析

1.答案为：B；

解析：

因为向量a，b是两个不共线的向量，所以若向量m=4a＋b与n=a－λb共线，

则4×(－λ)=1×1，解得λ=－，故选B．

2.答案为：D；

解析：

∵A，B，C三点共线，∴∥，设=m(m≠0)，则λa＋b=m(a＋μb)，

∴∴λμ=1，故选D．

3.答案为：C；

解析：

如图，∵=2，∴=＋=＋=＋(－)=＋．故选C．

4.答案为：A；

解析：=＋=＋＋=＋=＋(－)=－＋．故选A．

5.答案为：A；

解析：根据向量的运算法则，可得=－=－=－(＋)=－，故选A．

6.答案为：C；

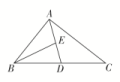
解析：

由平行四边形法则知＋=2，又由＋=4知2=4，即=2，

所以P为AD的中点，即点P与点F重合．故选C．

7.答案为：C；

解析：

=＋=＋=－＋＋＋=－＋＋＋

=－＋＋＋(＋＋)=－＋．故选C．

8.答案为：B；

因为=，所以=4.所以=m＋=m＋，

因为B，P，N共线，所以m＋=1，m=.

9.答案为：0；

解析：

因为＋=2，由平行四边形法则知，点P为AC的中点，故＋=0．

10.答案为：，－；

解析：

如图，在△ABC中，=＋＋=－＋＋=－＋＋(－)=－．

∴x=，y=－．

11.答案为：；

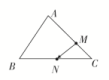
解析：∵=－=－=－2=3－2，

∴=λ＋3μ－2μ，∴(1－3μ)=(λ－2μ)，

∵和是不共线向量，∴解得∴λμ=.

12.答案为：；

解析：

设e1，e2分别为水平方向(向右)与竖直方向(向上)的单位向量，

则向量c=e1－2e2，a=2e1＋e2，b=－2e1－2e2，由c与xa＋yb共线，

得c=λ(xa＋yb)，所以e1－2e2=2λ(x－y)e1＋λ(x－2y)e2，

所以所以则的值为．

13.证明：=＋，①;=＋，②;=＋，③;=＋，④

∵O为平行四边形ABCD对角线的交点，∴==-，==-.

①＋②＋③＋④，得:4=＋＋＋＋(＋)＋(＋)=＋＋＋＋00，

∴＋＋＋=4.

14.解：

15.解：

16.证明：

(1)若m＋n=1，

则=m＋(1－m)

=＋m(－)，

∴－=m(－)，

即=m，∴与共线．

又∵与有公共点B，

∴A，P，B三点共线．

(2)若A，P，B三点共线，

则存在实数λ，使=λ，

∴－=λ(－)．

又=m＋n.

故有m＋(n－1)=λ－λ，

即(m－λ)＋(n＋λ－1)=0.

∵O，A，B不共线，∴，不共线，

∴∴m＋n=1.