高考数学一轮复习考点测试刷题本47 椭圆（含答案解析）

这是一份高考数学一轮复习考点测试刷题本47 椭圆（含答案解析），共8页。
2020高考数学(文数)考点测试刷题本47 椭圆 一         、选择题1.已知动点M(x，y)满足＋=4，则动点M的轨迹是(　　)A．椭圆          B．直线          C．圆         D．线段  2.已知椭圆C：＋=1的一个焦点为(2，0)，则C的离心率为(　　)A．         B．          C．        D．  3.已知中心在原点的椭圆C的右焦点为F(1，0)，离心率等于，则C的方程是(　　)A．＋=1        B．＋=1       C．＋=1        D．＋y2=1  4.已知椭圆C：＋=1(a>b>0)，若长轴长为6，且两焦点恰好将长轴三等分，则此椭圆的标准方程为(　　)A．＋=1       B．＋=1       C．＋=1         D．＋=1  5.椭圆的焦点在x轴上，中心在原点，其上、下顶点和两个焦点恰为边长是2的正方形的顶点，则椭圆的标准方程为(　　)A.＋=1         B.＋y2=1         C.＋=1          D.＋=1  6.设F1，F2为椭圆＋=1的两个焦点，点P在椭圆上，若线段PF1的中点在y轴上，则的值为(　　)A．           B．           C．             D．  7.已知点A(－1，0)和B(1，0)，动点P(x，y)在直线l：y=x＋3上移动，椭圆C以A，B为焦点且经过点P，则椭圆C的离心率的最大值为(　　)A．         B．        C．           D．  8.设P为椭圆C：＋=1上一点，F1，F2分别是椭圆C的左、右焦点，且△PF1F2的重心为G，若|PF1|∶|PF2|=3∶4，那么△GPF1的面积为(　　)A．24          B．12           C．8              D．6  二         、填空题9.若椭圆的方程为＋=1，且此椭圆的焦距为4，则实数a=________．  10.已知椭圆＋=1(a＞b＞0)的半焦距为c，且满足c2－b2＋ac＜0，则该椭圆的离心率e的取值范围是________．  11.如图，在平面直角坐标系xOy中，F是椭圆＋=1(a>b>0)的右焦点，直线y=与椭圆交于B，C两点，且∠BFC=90°，则该椭圆的离心率是________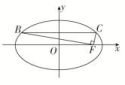．  12.设F1，F2是椭圆＋=1的两个焦点，P是椭圆上的点，且|PF1|∶|PF2|=4∶3，则△PF1F2的面积为________．  三         、解答题13.设O为坐标原点，动点M在椭圆C：＋y2=1(a＞1，a∈R)上，过O的直线交椭圆C于A，B两点，F为椭圆C的左焦点．(1)若△FAB的面积的最大值为1，求a的值；(2)若直线MA，MB的斜率乘积等于－，求椭圆C的离心率．              14.分别求出满足下列条件的椭圆的标准方程．(1)与椭圆＋=1有相同的离心率且经过点(2，－)；(2)已知点P在以坐标轴为对称轴的椭圆上，且P到两焦点的距离分别为5，3，过P且与长轴垂直的直线恰过椭圆的一个焦点．                 15.已知椭圆C：＋=1(a>2)，直线l：y=kx＋1(k≠0)与椭圆C相交于A，B两点，点D为AB的中点．(1)若直线l与直线OD(O为坐标原点)的斜率之积为－，求椭圆C的方程；(2)在(1)的条件下，y轴上是否存在定点M，使得当k变化时，总有∠AMO=∠BMO(O为坐标原点)？若存在，求出定点M的坐标；若不存在，请说明理由．                       16.已知椭圆＋=1(a>b>0)的离心率e=，原点到过点A(0，－b)和B(a，0)的直线的距离为．(1)求椭圆的方程；(2)设F1，F2为椭圆的左、右焦点，过F2作直线交椭圆于P，Q两点，求△PQF1内切圆半径r的最大值．                       
答案解析1.答案为：D；解析：设点F1(－2，0)，F2(2，0)，由题意知动点M满足|MF1|＋|MF2|=4=|F1F2|，故动点M的轨迹是线段F1F2．故选D．  2.答案为：C；解析：根据题意，可知c=2，因为b2=4，所以a2=b2＋c2=8，即a=2，所以椭圆C的离心率为e==．故选C．  3.答案为：C；解析：依题意，所求椭圆的焦点位于x轴上，且c=1，e=⇒a=2，b2=a2－c2=3，因此其方程是＋=1，故选C．  4.答案为：B；解析：椭圆长轴长为6，即2a=6，得a=3，∵两焦点恰好将长轴三等分，∴2c=·2a=2，得c=1，因此，b2=a2－c2=9－1=8，∴此椭圆的标准方程为＋=1．故选B．  5.答案为：C；由条件可知b=c=，a=2，所以椭圆的标准方程为＋=1.故选C.  6.答案为：B；解析：由题意知a=3，b=．由椭圆定义知|PF1|＋|PF2|=6．在△PF1F2中，因为PF1的中点在y轴上，O为F1F2的中点，由三角形中位线的性质可推得PF2⊥x轴，所以由x=c时可得|PF2|==，所以|PF1|=6－|PF2|=，所以=，故选B．  7.答案为：A；解析：A(－1，0)关于直线l：y=x＋3的对称点为A′(－3，2)，连接A′B交直线l于点P，则此时椭圆C的长轴长最短，为|A′B|=2，所以椭圆C的离心率的最大值为=．故选A．   8.答案为：C；解析：∵P为椭圆C：＋=1上一点，|PF1|∶|PF2|=3∶4，|PF1|＋|PF2|=2a=14，∴|PF1|=6，|PF2|=8，又∵|F1F2|=2c=2=10，∴易知△PF1F2是直角三角形，S△PF1F2=|PF1|·|PF2|=24，∵△PF1F2的重心为点G，∴S△PF1F2=3S△GPF1，∴△GPF1的面积为8，故选C． 9.答案为：4或8；解析：对椭圆的焦点位置进行讨论．由椭圆的焦距为4得c=2，当2<a<6时，椭圆的焦点在x轴上，则10－a－(a－2)=4，解得a=4；当6<a<10时，椭圆的焦点在y轴上，则a－2－(10－a)=4，解得a=8．故a=4或a=8．  10.答案为：；解析：∵c2－b2＋ac＜0，∴c2－(a2－c2)＋ac＜0，即2c2－a2＋ac＜0，∴2－1＋＜0，即2e2＋e－1＜0，解得－1＜e＜.又∵0＜e＜1，∴0＜e＜.∴椭圆的离心率e的取值范围是.  11.答案为：；解析：由已知条件易得B，C，F(c，0)，∴=c＋a，－，=c－a，－，由∠BFC=90°，可得·=0，所以＋2=0，c2－a2＋b2=0，即4c2－3a2＋(a2－c2)=0，亦即3c2=2a2，所以=，则e==．  12.答案为：24；解析：因为|PF1|＋|PF2|=14，又|PF1|∶|PF2|=4∶3，所以|PF1|=8，|PF2|=6.因为|F1F2|=10，所以PF1⊥PF2.所以S△PF1F2=|PF1|·|PF2|=×8×6=24.        13.解：(1)S△FAB=|OF|·|yA－yB|≤|OF|==1，所以a=.(2)由题意可设A(x0，y0)，B(－x0，－y0)，M(x，y)，则＋y2=1，＋y=1，kMA·kMB=·====－=－，所以a2=3，所以a=，所以c==，所以椭圆的离心率e===.  14.解：(1)由题意，设所求椭圆的方程为＋=t1或＋=t2(t1，t2＞0)，因为椭圆过点(2，－)，所以t1=＋=2，或t2=＋=.故所求椭圆的标准方程为＋=1或＋=1.(2)由于焦点的位置不确定，所以设所求的椭圆方程为＋=1(a＞b＞0)或＋=1(a＞b＞0)，由已知条件得解得a=4，c=2，所以b2=12.故椭圆方程为＋=1或＋=1.  15.解：(1)由得(4＋a2k2)x2＋2a2kx－3a2=0，显然Δ>0，设A(x1，y1)，B(x2，y2)，D(x0，y0)，则x1＋x2=－，x1x2=，∴x0=－，y0=－＋1=，∴k·=k·－=－，∴a2=8．∴椭圆C的方程为＋=1．(2)假设存在定点M符合题意，且设M(0，m)，由∠AMO=∠BMO得kAM＋kBM=0．∴＋=0．即y1x2＋y2x1－m(x1＋x2)=0，∴2kx1x2＋x1＋x2－m(x1＋x2)=0．由(1)知x1＋x2=－，x1x2=，∴－－＋=0，∴=0，即=0，∵k≠0，∴－4＋m=0，∴m=4．∴存在定点M(0，4)，使得∠AMO=∠BMO．16.解：(1)直线AB的方程为＋=1，即bx－ay－ab=0．原点到直线AB的距离为=，即3a2＋3b2=4a2b2，①由e==，得c2=a2，②又a2=b2＋c2，③所以联立①②③可得a2=3，b2=1，c2=2．故椭圆的方程为＋y2=1．(2)由(1)得F1(－，0)，F2(，0)，设P(x1，y1)，Q(x2，y2)．易知直线PQ的斜率不为0，故设其方程为x=ky＋，联立直线与椭圆的方程得消去x得(k2＋3)y2＋2ky－1=0．故④而S△PQF1=S△F1F2P＋S△F1F2Q=|F1F2||y1－y2|=，⑤将④代入⑤，得S△PQF1==．又S△PQF1=(|PF1|＋|F1Q|＋|PQ|)·r=2a·r=2r，所以=2r，故r==≤，当且仅当=，即k=±1时取等号．故△PQF1内切圆半径r的最大值为．