


所属成套资源:高考数学一轮复习作业本 (含答案)
高考数学一轮复习作业本8.4 椭圆(含答案)
展开
这是一份高考数学一轮复习作业本8.4 椭圆(含答案),共8页。
2020高考数学(理数)复习作业本8.4 椭圆一 、选择题1.已知椭圆+=1(a>b>0)的一个焦点是圆x2+y2-6x+8=0的圆心,且短轴长为8,则椭圆的左顶点为( )A.(-3,0) B.(-4,0) C.(-10,0) D.(-5,0) 2.设F1,F2分别为椭圆+=1的两个焦点,点P在椭圆上,若线段PF1的中点在y轴上,则的值为( )A. B. C. D. 3.已知方程![]() 表示焦点在y轴上的椭圆,则实数k的取值范围是( )A.(0.5,2) B.(1,+∞) C.(1,2) D.(0.5,1) 4.以椭圆短轴为直径的圆经过此椭圆的长轴的两个三等分点,则该椭圆的离心率是( )A. B. C. D. 5.如图,已知椭圆C的中心为原点O,F(-2
表示焦点在y轴上的椭圆,则实数k的取值范围是( )A.(0.5,2) B.(1,+∞) C.(1,2) D.(0.5,1) 4.以椭圆短轴为直径的圆经过此椭圆的长轴的两个三等分点,则该椭圆的离心率是( )A. B. C. D. 5.如图,已知椭圆C的中心为原点O,F(-2![]() ,0)为C的左焦点,P为C上一点,满足|OP|=|OF|,且|PF|=4,则椭圆C的方程为( )
,0)为C的左焦点,P为C上一点,满足|OP|=|OF|,且|PF|=4,则椭圆C的方程为( )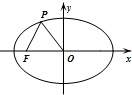 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6.如图,已知椭圆C的中心为原点O,F(-5,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=6,则椭圆C的方程为( )
6.如图,已知椭圆C的中心为原点O,F(-5,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=6,则椭圆C的方程为( )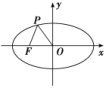 A.+=1 B.+=1 C.+=1 D.+=1 7.已知点F1,F2分别是椭圆E:
A.+=1 B.+=1 C.+=1 D.+=1 7.已知点F1,F2分别是椭圆E:![]() =1的左、右焦点,P为E上一点,直线1为∠F1PF2的外角平分线,过点F2作l的垂线,垂足为M,则|OM|=( )A.10 B.8 C.5 D.4 8.椭圆+=1的左焦点为F,直线x=a与椭圆相交于点M,N,当△FMN的周长最大时,△FMN的面积是( )A. B. C. D. 二 、填空题9.设椭圆C:
=1的左、右焦点,P为E上一点,直线1为∠F1PF2的外角平分线,过点F2作l的垂线,垂足为M,则|OM|=( )A.10 B.8 C.5 D.4 8.椭圆+=1的左焦点为F,直线x=a与椭圆相交于点M,N,当△FMN的周长最大时,△FMN的面积是( )A. B. C. D. 二 、填空题9.设椭圆C:![]() (a>b>0)的左、右焦点分别为F1,F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为 . 10.若椭圆+=1(a>b>0)的离心率为,短轴长为4,则椭圆的标准方程为________. 11.如图,在平面直角坐标系xOy中,F是椭圆
(a>b>0)的左、右焦点分别为F1,F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为 . 10.若椭圆+=1(a>b>0)的离心率为,短轴长为4,则椭圆的标准方程为________. 11.如图,在平面直角坐标系xOy中,F是椭圆![]() (a>b>0)的右焦点,直线y=
(a>b>0)的右焦点,直线y=![]() 与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是 .
与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是 . 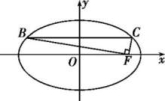 12.已知P为椭圆+=1(a>b>0)上一点,F1,F2是其左、右焦点,∠F1PF2 取最大值时,cos∠F1PF2=,则椭圆的离心率为________. 三 、解答题13.已知A(x0,0),B(0,y0)两点分别在x轴和y轴上运动,且|AB|=1,若动点P(x,y)满足=2+.(1)求动点P的轨迹C的标准方程;(2)直线l:x=ty+1与曲线C交于A,B两点,E(-1,0),试问:当t变化时,是否存在一条直线l,使△ABE的面积为2?若存在,求出直线l的方程;若不存在,说明理由. 14.已知焦点在y轴上的椭圆E的中心是原点O,离心率等于
12.已知P为椭圆+=1(a>b>0)上一点,F1,F2是其左、右焦点,∠F1PF2 取最大值时,cos∠F1PF2=,则椭圆的离心率为________. 三 、解答题13.已知A(x0,0),B(0,y0)两点分别在x轴和y轴上运动,且|AB|=1,若动点P(x,y)满足=2+.(1)求动点P的轨迹C的标准方程;(2)直线l:x=ty+1与曲线C交于A,B两点,E(-1,0),试问:当t变化时,是否存在一条直线l,使△ABE的面积为2?若存在,求出直线l的方程;若不存在,说明理由. 14.已知焦点在y轴上的椭圆E的中心是原点O,离心率等于![]() ,以椭圆E的长轴和短轴为对角线的四边形的周长为4
,以椭圆E的长轴和短轴为对角线的四边形的周长为4![]() .直线l:y=kx+m与y轴交于点P,与椭圆E相交于A、B两个点.(1)求椭圆E的方程;(2)若
.直线l:y=kx+m与y轴交于点P,与椭圆E相交于A、B两个点.(1)求椭圆E的方程;(2)若![]() =3
=3![]() ,求m2的取值范围. 15.已知椭圆+=1(a>b>0)的一个顶点为B(0,4),离心率e=,直线l交椭圆于M,N两点.(1)若直线l的方程为y=x-4,求弦MN的长;(2)如果△BMN的重心恰好为椭圆的右焦点F,求直线l方程的一般式. 16.已知椭圆C:+=1(a>b>0)的离心率为,左焦点为F(-1,0),过点D(0,2)且斜率为k的直线l交椭圆于A,B两点.(1)求椭圆C的标准方程;(2)在y轴上,是否存在定点E,使·恒为定值?若存在,求出E点的坐标和这个定值;若不存在,说明理由.
,求m2的取值范围. 15.已知椭圆+=1(a>b>0)的一个顶点为B(0,4),离心率e=,直线l交椭圆于M,N两点.(1)若直线l的方程为y=x-4,求弦MN的长;(2)如果△BMN的重心恰好为椭圆的右焦点F,求直线l方程的一般式. 16.已知椭圆C:+=1(a>b>0)的离心率为,左焦点为F(-1,0),过点D(0,2)且斜率为k的直线l交椭圆于A,B两点.(1)求椭圆C的标准方程;(2)在y轴上,是否存在定点E,使·恒为定值?若存在,求出E点的坐标和这个定值;若不存在,说明理由.
答案解析1.答案为:D.解析:∵圆的标准方程为(x-3)2+y2=1,∴圆心坐标为(3,0),∴c=3.又b=4,∴a==5.∵椭圆的焦点在x轴上,∴椭圆的左顶点为(-5,0). 2.答案为:B.解析:由题意知a=3,b=,c=2.设线段PF1的中点为M,则有OM∥PF2,因为OM⊥F1F2,所以PF2⊥F1F2,所以|PF2|==.又因为|PF1|+|PF2|=2a=6,所以|PF1|=2a-|PF2|=,所以=×=,故选B.3.答案为:C; 4.答案为:D.解析:不妨令椭圆方程为+=1(a>b>0).因为以椭圆短轴为直径的圆经过此椭圆的长轴的两个三等分点,所以2b=,即a=3b,则c==2b,则该椭圆的离心率e==.故选D.5.答案为:B;
4.答案为:D.解析:不妨令椭圆方程为+=1(a>b>0).因为以椭圆短轴为直径的圆经过此椭圆的长轴的两个三等分点,所以2b=,即a=3b,则c==2b,则该椭圆的离心率e==.故选D.5.答案为:B; 6.答案为:C.解析:由题意可得c=5,设右焦点为F′,连接PF′,由|OP|=|OF|=|OF′|知,∠PFF′=∠FPO,∠OF′P=∠OPF′,∴∠PFF′+∠OF′P=∠FPO+∠OPF′,∴∠FPO+∠OPF′=90°,即PF⊥PF′.在Rt△PFF′中,由勾股定理,得|PF′|===8,由椭圆定义,得|PF|+|PF′|=2a=6+8=14,从而a=7,得a2=49,于是b2=a2-c2=72-52=24,所以椭圆C的方程为+=1,故选C. 7.C.8.答案为:C.解析:设椭圆的右焦点为E,由椭圆的定义知△FMN的周长为L=|MN|+|MF|+|NF|=|MN|+(2-|ME|)+(2-|NE|).因为|ME|+|NE|≥|MN|,所以|MN|-|ME|-|NE|≤0,当直线MN过点E时取等号,所以L=4+|MN|-|ME|-|NE|≤4,即直线x=a过椭圆的右焦点E时,△FMN的周长最大,此时S△FMN=×|MN|×|EF|=××2=,故选C.9.答案为:
6.答案为:C.解析:由题意可得c=5,设右焦点为F′,连接PF′,由|OP|=|OF|=|OF′|知,∠PFF′=∠FPO,∠OF′P=∠OPF′,∴∠PFF′+∠OF′P=∠FPO+∠OPF′,∴∠FPO+∠OPF′=90°,即PF⊥PF′.在Rt△PFF′中,由勾股定理,得|PF′|===8,由椭圆定义,得|PF|+|PF′|=2a=6+8=14,从而a=7,得a2=49,于是b2=a2-c2=72-52=24,所以椭圆C的方程为+=1,故选C. 7.C.8.答案为:C.解析:设椭圆的右焦点为E,由椭圆的定义知△FMN的周长为L=|MN|+|MF|+|NF|=|MN|+(2-|ME|)+(2-|NE|).因为|ME|+|NE|≥|MN|,所以|MN|-|ME|-|NE|≤0,当直线MN过点E时取等号,所以L=4+|MN|-|ME|-|NE|≤4,即直线x=a过椭圆的右焦点E时,△FMN的周长最大,此时S△FMN=×|MN|×|EF|=××2=,故选C.9.答案为:![]() .10.答案为:+=1;解析:由题意可知e==,2b=4,得b=2,所以解得所以椭圆的标准方程为+=1.11.答案为:
.10.答案为:+=1;解析:由题意可知e==,2b=4,得b=2,所以解得所以椭圆的标准方程为+=1.11.答案为:![]() ;
;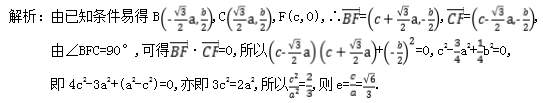 12.答案为:;解析:易知∠F1PF2取最大值时,点P为椭圆+=1与y轴的交点,由余弦定理及椭圆的定义得2a2-=4c2,即a=c,所以椭圆的离心率e==.13.解:(1)因为=2+,即(x,y)=2(x0,0)+(0,y0)=(2x0,y0),所以x=2x0,y=y0,所以x0=x,y0=y,又|AB|=1,所以x+y=1,即+=1,即+=1,所以动点P的轨迹C的标准方程为+=1.(2)由方程组得(3t2+4)y2+6ty-9=0,设A(x1,y1),B(x2,y2),则y1+y2=-,y1y2=-<0,所以|y1-y2|===.因为直线x=ty+1过点F(1,0),所以S△ABE=|EF||y1-y2|=×2×=,令=2,则t2=-,不成立,故不存在满足题意的直线l.14.解:
12.答案为:;解析:易知∠F1PF2取最大值时,点P为椭圆+=1与y轴的交点,由余弦定理及椭圆的定义得2a2-=4c2,即a=c,所以椭圆的离心率e==.13.解:(1)因为=2+,即(x,y)=2(x0,0)+(0,y0)=(2x0,y0),所以x=2x0,y=y0,所以x0=x,y0=y,又|AB|=1,所以x+y=1,即+=1,即+=1,所以动点P的轨迹C的标准方程为+=1.(2)由方程组得(3t2+4)y2+6ty-9=0,设A(x1,y1),B(x2,y2),则y1+y2=-,y1y2=-<0,所以|y1-y2|===.因为直线x=ty+1过点F(1,0),所以S△ABE=|EF||y1-y2|=×2×=,令=2,则t2=-,不成立,故不存在满足题意的直线l.14.解: 15.解:
15.解: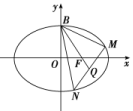 (1)由已知得b=4,且=,即=,∴=,解得a2=20,∴椭圆方程为+=1.则4x2+5y2=80与y=x-4联立,消去y得9x2-40x=0,∴x1=0,x2=,∴所求弦长|MN|=|x2-x1|=.(2)设椭圆右焦点F的坐标为(2,0),线段MN的中点为Q(x0,y0),由三角形重心的性质知=2,又B(0,4),∴(2,-4)=2(x0-2,y0),故得x0=3,y0=-2,即得Q的坐标为(3,-2).设M(x1,y1),N(x2,y2),则x1+x2=6,y1+y2=-4,且+=1,+=1,以上两式相减得+=0,∴kMN==-·=-×=,故直线MN的方程为y+2=(x-3),即6x-5y-28=0.16.解:(1)由已知可得可得a2=2,b2=1,所以椭圆C的标准方程为+y2=1.(2)设过点D(0,2)且斜率为k的直线l的方程为y=kx+2,由消去y整理得(1+2k2)x2+8kx+6=0,设A(x1,y1),B(x2,y2),则x1+x2=-,x1x2=.又y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4=-,y1+y2=(kx1+2)+(kx2+2)=k(x1+x2)+4=.设存在点E(0,m),则=(-x1,m-y1),=(-x2,m-y2),所以·=x1x2+m2-m(y1+y2)+y1y2=+m2-m×-=.要使·=t(t为常数),只需=t,从而(2m2-2-2t)k2+m2-4m+10-t=0,即解得m=,从而t=,故存在定点E,使·恒为定值.
(1)由已知得b=4,且=,即=,∴=,解得a2=20,∴椭圆方程为+=1.则4x2+5y2=80与y=x-4联立,消去y得9x2-40x=0,∴x1=0,x2=,∴所求弦长|MN|=|x2-x1|=.(2)设椭圆右焦点F的坐标为(2,0),线段MN的中点为Q(x0,y0),由三角形重心的性质知=2,又B(0,4),∴(2,-4)=2(x0-2,y0),故得x0=3,y0=-2,即得Q的坐标为(3,-2).设M(x1,y1),N(x2,y2),则x1+x2=6,y1+y2=-4,且+=1,+=1,以上两式相减得+=0,∴kMN==-·=-×=,故直线MN的方程为y+2=(x-3),即6x-5y-28=0.16.解:(1)由已知可得可得a2=2,b2=1,所以椭圆C的标准方程为+y2=1.(2)设过点D(0,2)且斜率为k的直线l的方程为y=kx+2,由消去y整理得(1+2k2)x2+8kx+6=0,设A(x1,y1),B(x2,y2),则x1+x2=-,x1x2=.又y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4=-,y1+y2=(kx1+2)+(kx2+2)=k(x1+x2)+4=.设存在点E(0,m),则=(-x1,m-y1),=(-x2,m-y2),所以·=x1x2+m2-m(y1+y2)+y1y2=+m2-m×-=.要使·=t(t为常数),只需=t,从而(2m2-2-2t)k2+m2-4m+10-t=0,即解得m=,从而t=,故存在定点E,使·恒为定值.
相关试卷
这是一份高考数学一轮复习作业本8.2 圆的方程(含答案),共5页。
这是一份高考数学一轮复习作业本1.1 集合(含答案),共3页。
这是一份高考数学一轮复习夯基练习:椭圆(含答案),共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。











