高考数学一轮复习夯基练习：椭圆(含答案)

这是一份高考数学一轮复习夯基练习：椭圆(含答案)，共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
夯基练习 椭圆一 、选择题1.设椭圆C：＋=1(a>b>0)的左、右焦点分别为F1，F2，P是C上的点，PF2⊥F1F2，∠PF1F2=30°，则C的离心率为(　　)A.　　         B.　         C.　            D.  2.已知直线l：x＋y－3=0，椭圆＋y2=1，则直线与椭圆的位置关系是(　　)A.相交           B.相切            C.相离           D.相切或相交  3.已知点A(－1，0)和B(1，0)，动点P(x，y)在直线l：y=x＋3上移动，椭圆C以A，B为焦点且经过点P，则椭圆C的离心率的最大值为(　　)A．         B．        C．           D．  4.已知椭圆C的左、右焦点坐标分别是(－，0)，(，0)，离心率是，则椭圆C的方程为(　　)A.＋y2=1         B.x2＋=1         C.＋=1         D.＋=1  5.已知中心在原点的椭圆C的右焦点为F(1，0)，离心率等于，则C的方程是(　　)A．＋=1        B．＋=1       C．＋=1        D．＋y2=1  6.设F1，F2为椭圆＋=1的两个焦点，点P在椭圆上，若线段PF1的中点在y轴上，则的值为(　　)A．           B．           C．             D．  7.椭圆＋=1的离心率为(　　)A.             B.            C.           D.  8.已知椭圆＋=1(a＞b＞0)的一个焦点是圆x2＋y2－6x＋8=0的圆心，且短轴长为8，则椭圆的左顶点为(　　)A．(－3，0)　          B．(－4，0)        C．(－10，0)           D．(－5，0)  9.已知椭圆C：＋=1(a>b>0)的左、右顶点分别为A1，A2，且以线段A1A2为直径的圆与直线bx－ay＋2ab=0相切，则C的离心率为(　　)A.           B.               C.             D.  10.斜率为1的直线l与椭圆＋y2=1相交于A，B两点，则|AB|的最大值为(　　)A．2             B.             C.           D.  11.已知椭圆(0<b<2)的左,右焦点分别为F1,F2,过F1的直线l交椭圆于A,B两点,若|BF2|+|AF2|的最大值为5,则b的值是(　　)A.1                           B.                            C.1.5                                     D.12.椭圆＋=1的左焦点为F，直线x=a与椭圆相交于点M，N，当△FMN的周长最大时，△FMN的面积是(　　)A.            B．          C.            D．   二 、填空题13.曲线＋=1与曲线＋=1(k<9)的________相等.(填“长轴长”或“短轴长”或“离心率”或“焦距”)14.若椭圆的方程为＋=1，且此椭圆的焦距为4，则实数a=________．  15.已知椭圆的中心在原点，一个焦点为F(3,0)，若以其四个顶点为顶点的四边形的面积是40，则该椭圆的方程是________.  16.已知椭圆C的中心在原点,一个焦点为F(-2,0),且长轴长与短轴长的比是2:,则椭圆C的方程是　　　　　　　　.  三 、解答题17.设直线y=x＋b与椭圆＋y2=1相交于A，B两个不同的点.(1)求实数b的取值范围；(2)当b=1时，求|AB|.          18.已知动圆M过定点A(－3,0)，并且内切于定圆B：(x－3)2＋y2=64，求动圆圆心M的轨迹方程.            19.已知椭圆C:的离心率为，且经过点(1.5,0.5).              (1)求椭圆C的方程；              (2)过点P(0，2)的直线交椭圆C于A，B两点，求△AOB(O为原点)面积的最大值.                  20.已知椭圆C：经过点，离心率，直线l的方程为 x=4.                                          (1)求椭圆C的方程；                                          (2)经过椭圆右焦点e的任一直线(不经过点a=﹣1)与椭圆交于两点A，B，设直线AB与l相交于点M,记PA，PB，PM的斜率分别为k1，k2，k3，问：k1+k2﹣2k3是否为定值，若是，求出此定值;                                          若不是，请说明理由.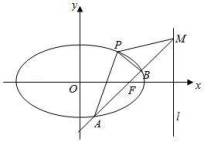                                               
参考答案1.答案为：D；解析：法一：由题意可设|PF2|=m，结合条件可知|PF1|=2m，|F1F2|=m，故离心率e=====.法二：由PF2⊥F1F2可知P点的横坐标为c，将x=c代入椭圆方程可解得y=±，所以|PF2|=.又由∠PF1F2=30°可得|F1F2|=|PF2|，故2c=·，变形可得(a2－c2)=2ac，等式两边同除以a2，得(1－e2)=2e，解得e=或e=－(舍去).  2.答案为：C；解析：把x＋y－3=0代入＋y2=1得＋(3－x)2=1，即5x2－24x＋32=0.∵Δ=242－4×5×32=－64＜0，∴直线与椭圆相离.  3.答案为：A；解析：A(－1，0)关于直线l：y=x＋3的对称点为A′(－3，2)，连接A′B交直线l于点P，则此时椭圆C的长轴长最短，为|A′B|=2，所以椭圆C的离心率的最大值为=．故选A．  4.答案为：A；解析：∵=，且c=，∴a=，b==1.∴椭圆方程为＋y2=1.  5.答案为：C；解析：依题意，所求椭圆的焦点位于x轴上，且c=1，e=⇒a=2，b2=a2－c2=3，因此其方程是＋=1，故选C．  6.答案为：B；解析：由题意知a=3，b=．由椭圆定义知|PF1|＋|PF2|=6．在△PF1F2中，因为PF1的中点在y轴上，O为F1F2的中点，由三角形中位线的性质可推得PF2⊥x轴，所以由x=c时可得|PF2|==，所以|PF1|=6－|PF2|=，所以=，故选B．  7.答案为：D；解析：由＋=1可得a2=16，b2=8，∴c2=a2－b2=8.∴e2==.∴e=.  8.答案为：D.解析：∵圆的标准方程为(x－3)2＋y2=1，∴圆心坐标为(3，0)，∴c=3.又b=4，∴a==5.∵椭圆的焦点在x轴上，∴椭圆的左顶点为(－5，0)．  9.答案为：A；解析：以线段A1A2为直径的圆的方程为x2＋y2=a2，由原点到直线bx－ay＋2ab=0的距离d==a，得a2=3b2，所以C的离心率e= =.  10.答案为：C；设A，B两点的坐标分别为(x1，y1)，(x2，y2)，直线l的方程为y=x＋t，由消去y，得5x2＋8tx＋4(t2－1)=0，则x1＋x2=－t，x1x2=.∴|AB|=|x1－x2|=·=· =·，当t=0时，|AB|max=.  11.答案为：D；12.答案为：C.解析：设椭圆的右焦点为E，由椭圆的定义知△FMN的周长为L=|MN|＋|MF|＋|NF|=|MN|＋(2－|ME|)＋(2－|NE|)．因为|ME|＋|NE|≥|MN|，所以|MN|－|ME|－|NE|≤0，当直线MN过点E时取等号，所以L=4＋|MN|－|ME|－|NE|≤4，即直线x=a过椭圆的右焦点E时，△FMN的周长最大，此时S△FMN=×|MN|×|EF|=××2=，故选C.   二 、填空题13.答案为：焦距解析：c2=25－k－(9－k)=16，c=4.故两条曲线有相同的焦距.14.答案为：4或8；解析：对椭圆的焦点位置进行讨论．由椭圆的焦距为4得c=2，当2<a<6时，椭圆的焦点在x轴上，则10－a－(a－2)=4，解得a=4；当6<a<10时，椭圆的焦点在y轴上，则a－2－(10－a)=4，解得a=8．故a=4或a=8．  15.答案为：＋=1；解析：以椭圆顶点为顶点的四边形是对角线长分别为2a和2b的菱形，因此其面积为S=·2a·2b=2ab=40，∴ab=20.又c=3，且a2－b2=c2.∴a2－=9，a4－9a2－400=0.∴a2=25或a2=－16(舍去).∴a=5，b=4，所求方程为＋=1.  16.答案为：+=1； 三 、解答题17.解：(1)将y=x＋b代入＋y2=1，消去y，整理得3x2＋4bx＋2b2－2=0.①因为直线y=x＋b与椭圆＋y2=1相交于A，B两个不同的点，所以Δ=16b2－12(2b2－2)=24－8b2>0，解得－<b<.所以b的取值范围为(－，).(2)设A(x1，y1)，B(x2，y2)，当b=1时，方程①为3x2＋4x=0.解得x1=0，x2=－.相应地y1=1，y2=－.所以|AB|==.  18.解：设动圆M的半径为r，则|MA|=r，|MB|=8－r，∴|MA|＋|MB|=8，且8>|AB|=6，∴动点M的轨迹是椭圆，且焦点分别是A(－3,0)，B(3,0)，且2a=8，∴a=4，c=3，∴b2=a2－c2=16－9=7.∴所求动圆圆心M的轨迹方程是＋=1. 19.                                                                                                                                20.解：