高考数学一轮复习作业本8.6 抛物线（含答案）

这是一份高考数学一轮复习作业本8.6 抛物线（含答案），共8页。
2020高考数学(理数)复习作业本8.6 抛物线一         、选择题1.已知抛物线y2=2px(p>0),过其焦点且斜率为-1的直线交抛物线于A,B两点,若线段AB的中点的横坐标为3,则该抛物线的准线方程为(　　) A.x=1                           B.x=2               C.x=-1                          D.x=-2 2.过抛物线x2=4y的焦点F作直线AB,CD与抛物线交于A,B,C,D四点,且AB⊥CD,则·+·的最大值等于(　　)A.-4                B.-16             C.4                            D.-8 3.设F为抛物线C:y2=4x的焦点,曲线(k>0)与C交于点P,PF⊥x轴,则k=(　　)A.0.5                          B.1                           C.1.5                             D.2 4.设抛物线C:y2=4x的焦点为F,直线l过F且与C交于A,B两点.若|AF|=3|BF|,则l的方程为(　　)A.y=x-1或y=-x+1                      B.y=(x-1)或y=-(x-1)     C.y=(x-1)或y=-(x-1)           D.y=(x-1)或y=-(x-1) 5.已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点.若=4,则|QF|=(　　)　　　　　　 　　　　　　 　　　　　　 A.3.5                            B.3              C.2.5              D.2 6.已知过抛物线C：y2=8x的焦点F的直线l交抛物线于P，Q两点，若R为线段PQ的中点，连接OR并延长交抛物线C于点S，则的取值范围是(　　)A．(0，2)           B．[2，＋∞)      C．(0，2]           D．(2，＋∞)  7.已知抛物线y2=8x，点Q是圆C：x2＋y2＋2x－8y＋13=0上任意一点，记抛物线上任意一点P到直线x=－2的距离为d，则|PQ|＋d的最小值为(　　)A．5             B．4             C．3             D．2    8.已知A，B两点均在焦点为F的抛物线y2=2px(p＞0)上，若|AF|+|BF|=4，线段AB的中点到直线x=的距离为1，则P的值为(     )                                          A.1            B.1或3                          C.2                          D.2或6 二         、填空题9.已知点P在抛物线y2=4x上,且点P到y轴的距离与其到焦点的距离之比为,则点P到x轴的距离为　　　　.  10.抛物线C：y2=2px(p＞0)的焦点为F，点O是坐标原点，过点O，F的圆与抛物线C的准线相切，且该圆的面积为36π，则抛物线的方程为________． 11.若抛物线y2=2px(p>0)的准线经过双曲线x2-y2=1的一个焦点,则p=　　　　.  12.已知抛物线C：x2=4y的焦点为F，直线AB与抛物线C相交于A，B两点，若2＋－3=0，则弦AB中点到抛物线C的准线的距离为________． 三         、解答题13.如图所示,已知抛物线C:y2=4x的焦点为F,直线l经过点F且与抛物线C相交于A、B两点.(1)若线段AB的中点在直线y=2上,求直线l的方程;(2)若线段|AB|=20,求直线l的方程.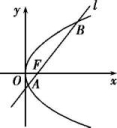               14.已知抛物线C：x2=2py(p＞0)和定点M(0，1)，设过点M的动直线交抛物线C于A，B两点，抛物线C在A，B处的切线的交点为N.(1)若N在以AB为直径的圆上，求p的值；(2)若△ABN的面积的最小值为4，求抛物线C的方程．                15.已知抛物线C：y2=2px过点P(1，1)．过点作直线l与抛物线C交于不同的两点M，N，过点M作x轴的垂线分别与直线OP，ON交于点A，B，其中O为原点．(1)求抛物线C的方程，并求其焦点坐标和准线方程；(2)求证：A为线段BM的中点．                         16.已知过抛物线y2=2px(p>0)的焦点,斜率为的直线交抛物线于A(x1,y1),B(x2,y2)(x1<x2)两点,且|AB|=9.(1)求该抛物线的方程;(2)O为坐标原点,C为抛物线上一点,若=+λ,求λ的值.    
答案解析1.答案为：C；2.答案为：B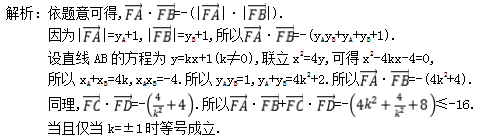；3.答案为：D；4.答案为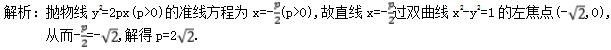：；5.答案为：B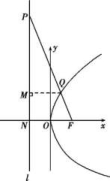；  6.答案为：D.解析：由题意知，抛物线y2=8x的焦点F的坐标为(2，0)，直线l的斜率存在且不为0，设直线l的方程为y=k(x－2)．由消去y整理得k2x2－4(k2＋2)x＋4k2=0，设P(x1，y1)，Q(x2，y2)，R(x0，y0)，S(x3，y3)，则x1＋x2=，故x0==，y0=k(x0－2)=，所以kOS==，直线OS的方程为y=x，代入抛物线方程，解得x3=，由条件知k2＞0.所以==k2＋2＞2.选D. 7.答案为：C.解析：如图，由题意知抛物线y2=8x的焦点为F(2，0)，连接PF，FQ，则d=|PF|，将圆C的方程化为(x＋1)2＋(y－4)2=4，圆心为C(－1，4)，半径为2，则|PQ|＋d=|PQ|＋|PF|，又|PQ|＋|PF|≥|FQ|(当且仅当F，P，Q三点共线时取得等号)．所以当F，Q，C三点共线时取得最小值，且为|CF|－|CQ|=－2=3，故选C.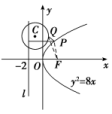8.B.9.答案为：；10.答案为：y2=16x；解析：设满足题意的圆的圆心为M.根据题意可知圆心M在抛物线上，又因为圆的面积为36π，所以圆的半径为6，则|MF|=xM＋=6，即xM=6－，又由题意可知xM=，所以=6－，解得p=8.所以抛物线方程为y2=16x.11.答案为：2；12.答案为：2.25；解析：依题意得，抛物线的焦点为F(0，1)，准线方程是y=－1，因为2(－)＋(－)=0，即2＋=0，所以F，A，B三点共线．设直线AB：y=kx＋1(k≠0)，A(x1，y1)，B(x2，y2)，则由得x2=4(kx＋1)，即x2－4kx－4=0，x1x2=－4　①；又2＋=0，因此2x1＋x2=0　②.由①②解得x=2，弦AB的中点到抛物线C的准线的距离为：[(y1＋1)＋(y2＋1)]=(y1＋y2)＋1=(x＋x)＋1=＋1=.13.解：14.解：由题意知，直线AB的斜率一定存在，∴设直线AB：y=kx＋1，A(x1，y1)，B(x2，y2)，将直线AB的方程代入抛物线C的方程得x2－2pkx－2p=0，则x1＋x2=2pk，x1x2=－2p.①(1)由x2=2py得y′=，则A，B处的切线斜率的乘积为=－，∵点N在以AB为直径的圆上，∴AN⊥BN，∴－=－1，∴p=2.(2)易得直线AN：y－y1=(x－x1)，直线BN：y－y2=(x－x2)，联立，得结合①式，解得即N(pk，－1)．|AB|=|x2－x1|==，点N到直线AB的距离d==，则S△ABN=·|AB|·d=≥2，当k=0时，取等号，∵△ABN的面积的最小值为4，∴2=4，∴p=2，故抛物线C的方程为x2=4y. 15.解：(1)把P(1，1)代入y2=2px得p=，所以抛物线C：y2=x，所以焦点坐标为，准线：x=－.(2)证明：设l：y=kx＋，M(x1，y1)，N(x2，y2)，OP：y=x，ON：y=x，由题知A(x1，x1)，B，由消去y得k2x2＋(k－1)x＋=0，所以x1＋x2=，x1·x2=.所以y1＋=kx1＋＋=2kx1＋，由x1＋x2=，x1x2=，上式=2kx1＋=2kx1＋(1－k)·2x1=2x1，所以A为线段BM的中点． 16.解：