


所属成套资源:高考数学一轮复习作业本 (含答案)
高考数学一轮复习作业本8.7 圆锥曲线的综合问题(含答案)
展开
这是一份高考数学一轮复习作业本8.7 圆锥曲线的综合问题(含答案),共8页。
2020高考数学(理数)复习作业本8.7 圆锥曲线的综合问题1.在圆x2+y2=3上任取一动点P,过P作x轴的垂线PD,D为垂足,![]() =
=![]()
![]() 动点M的轨迹为曲线C. (1)求C的方程及其离心率; (2)若直线l交曲线C交于A,B两点,且坐标原点到直线l的距离为
动点M的轨迹为曲线C. (1)求C的方程及其离心率; (2)若直线l交曲线C交于A,B两点,且坐标原点到直线l的距离为![]() ,求△AOB面积的最大值. 2.已知椭圆
,求△AOB面积的最大值. 2.已知椭圆![]() =1(a>b>0)过点
=1(a>b>0)过点![]() ,离心率为
,离心率为![]() .(1)求椭圆的标准方程;(2)过椭圆的上顶点作直线l交抛物线x2=2y于A、B两点,O为原点.①求证:OA⊥OB;②设OA、OB分别与椭圆相交于C、D两点,过原点O作直线CD的垂线OH,垂足为H。证明:|OH|为定值. 3.已知椭圆C:
.(1)求椭圆的标准方程;(2)过椭圆的上顶点作直线l交抛物线x2=2y于A、B两点,O为原点.①求证:OA⊥OB;②设OA、OB分别与椭圆相交于C、D两点,过原点O作直线CD的垂线OH,垂足为H。证明:|OH|为定值. 3.已知椭圆C:![]() 经过点
经过点![]() ,离心率
,离心率![]() ,直线l的方程为 x=4. (1)求椭圆C的方程; (2)经过椭圆右焦点e的任一直线(不经过点a=﹣1)与椭圆交于两点A,B,设直线AB与l相交于点M,记PA,PB,PM的斜率分别为k1,k2,k3,问:k1+k2﹣2k3是否为定值,若是,求出此定值; 若不是,请说明理由.
,直线l的方程为 x=4. (1)求椭圆C的方程; (2)经过椭圆右焦点e的任一直线(不经过点a=﹣1)与椭圆交于两点A,B,设直线AB与l相交于点M,记PA,PB,PM的斜率分别为k1,k2,k3,问:k1+k2﹣2k3是否为定值,若是,求出此定值; 若不是,请说明理由. 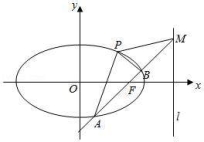 4.已知椭圆C:
4.已知椭圆C:![]() 的离心率为
的离心率为![]() ,且经过点(1.5,0.5). (1)求椭圆C的方程; (2)过点P(0,2)的直线交椭圆C于A,B两点,求△AOB(O为原点)面积的最大值. 5.已知椭圆C:
,且经过点(1.5,0.5). (1)求椭圆C的方程; (2)过点P(0,2)的直线交椭圆C于A,B两点,求△AOB(O为原点)面积的最大值. 5.已知椭圆C:![]() 的左、右焦点分别为F1、F2,上顶点为A.动直线
的左、右焦点分别为F1、F2,上顶点为A.动直线![]() :
:![]() 经过点F2,且△AF1F2是等腰直角三角形.(1)求椭圆C的标准方程;(2)设直线
经过点F2,且△AF1F2是等腰直角三角形.(1)求椭圆C的标准方程;(2)设直线![]() 交C于M、N两点,若点A在以线段MN为直径的圆外,求实数m的取值范围. 6.已知椭圆
交C于M、N两点,若点A在以线段MN为直径的圆外,求实数m的取值范围. 6.已知椭圆![]() 的离心率为
的离心率为![]() ,且点P(2,1)为椭圆上一点.(1)求椭圆的标准方程;(2)若直线
,且点P(2,1)为椭圆上一点.(1)求椭圆的标准方程;(2)若直线![]() 的斜率为0.5,直线
的斜率为0.5,直线![]() 与椭圆C交于A,B两点,求△PAB的面积的最大值. 7.如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,
与椭圆C交于A,B两点,求△PAB的面积的最大值. 7.如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,![]() ,直线y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M,N两点(M,N不重合),且|CM|=|DN|.(1)求椭圆E的离心率;(2)若m>0,设直线AD、BC的斜率分别为
,直线y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M,N两点(M,N不重合),且|CM|=|DN|.(1)求椭圆E的离心率;(2)若m>0,设直线AD、BC的斜率分别为![]() ,求
,求![]() 的取值范围.
的取值范围. 8.设O为坐标原点,动点M在椭圆C
8.设O为坐标原点,动点M在椭圆C![]() 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足![]() .(1)求点P的轨迹方程;(2)设点 在直线x=-3上,且
.(1)求点P的轨迹方程;(2)设点 在直线x=-3上,且![]() .证明过点P且垂直于OQ的直线l过C的左焦点F.
.证明过点P且垂直于OQ的直线l过C的左焦点F.
答案解析1.解: 2.解:
2.解: 3.解:
3.解: 4.
4. 5.解:
5.解: 6.解:
6.解: 7.解:
7.解:
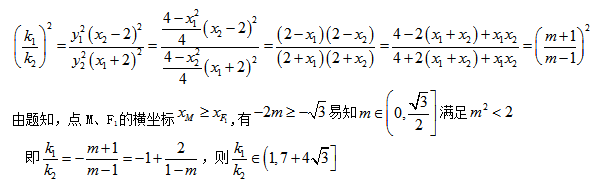 8.解:
8.解:
相关试卷
这是一份高考数学一轮复习夯基练习:圆锥曲线的综合问题(含答案),共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份高考数学(理数)一轮复习检测卷:8.7《直线与圆锥曲线的综合问题》 (学生版),共4页。试卷主要包含了已知抛物线C,若双曲线E等内容,欢迎下载使用。
这是一份高考数学(理数)一轮复习检测卷:8.7《直线与圆锥曲线的综合问题》 (教师版)











