


所属成套资源:高考数学一轮复习作业本 (含答案)
高考数学一轮复习作业本5.4 数列求和及综合应用(含答案)
展开
这是一份高考数学一轮复习作业本5.4 数列求和及综合应用(含答案),共7页。
2020高考数学(理数)复习作业本5.4 数列求和及综合应用1.已知数列{an}的通项公式为an=n2-5n+4.(1)数列中有多少项是负数?(2)n为何值时,an有最小值?并求出最小值. 2.设数列{an}的前![]() 项积为Tn,且Tn+2an=2(n∈N*).(1)求证:数列{
项积为Tn,且Tn+2an=2(n∈N*).(1)求证:数列{![]() }是等差数列.(2)设bn=(1-an)(1-an+1),求数列{bn}的前n项和Sn. 3. (设{an}为等比数列,Tn=na1+(n-1)a2+…+2an-1+an,已知T1=1,T2=4.(1)求数列{an}的首项和公比;(2)求数列{Tn}的通项公式. 4.已知等差数列{an}的公差为2,且
}是等差数列.(2)设bn=(1-an)(1-an+1),求数列{bn}的前n项和Sn. 3. (设{an}为等比数列,Tn=na1+(n-1)a2+…+2an-1+an,已知T1=1,T2=4.(1)求数列{an}的首项和公比;(2)求数列{Tn}的通项公式. 4.已知等差数列{an}的公差为2,且![]() ,
, ![]() ,
, ![]() 成等比数列.(1)求数列{an}的通项公式;(2)设数列
成等比数列.(1)求数列{an}的通项公式;(2)设数列![]() 的前项和为
的前项和为![]() ,求证:
,求证: ![]() . 5.已知数列{an}的前n项和为
. 5.已知数列{an}的前n项和为![]() ,且满足
,且满足![]() =
=![]()
(1)求![]() 的值;
的值; ![]()
(2)求数列{an}的通项公式及其前 n项和![]() . 6.已知数列
. 6.已知数列![]() 满足:
满足:![]() ,
,![]() 。数列
。数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() .⑴求数列
.⑴求数列![]() 、
、![]() 的通项公式;⑵令数列
的通项公式;⑵令数列![]() 满足
满足![]() ,求其前n项和为
,求其前n项和为![]() 7.已知{an}是正数组成的数列,a1=1,且点
7.已知{an}是正数组成的数列,a1=1,且点![]() (
(![]() )在函数
)在函数![]() 的图象上.(1)求数列{an}的通项公式;(2)若数列{bn}满足
的图象上.(1)求数列{an}的通项公式;(2)若数列{bn}满足![]() ,
,![]() ,求证:
,求证:![]() . 8.已知数列{an}是等比数列,
. 8.已知数列{an}是等比数列,![]() 为数列{an}的前
为数列{an}的前![]() 项和,且
项和,且![]() (1)求数列{an}的通项公式.(2)设
(1)求数列{an}的通项公式.(2)设![]() 且{bn}为递增数列.若
且{bn}为递增数列.若![]() 求证:
求证:![]()
答案解析1.解:(1)令n2-5n+4<0,得1<n<4,∵n∈N*,∴n=2或3.故数列中有两项是负数.即a2、a3为负数.(2)an=n2-5n+4=(n-2.5)2-2.25.∵n∈N*,∴当n=2或3时,an最小,最小值为-2.∴an+1-an=3-![]() -3+
-3+![]() =
=![]() -
-![]() =
=![]() >0,∴an+1>an.故数列{an}为递增数列. 2.解:
>0,∴an+1>an.故数列{an}为递增数列. 2.解: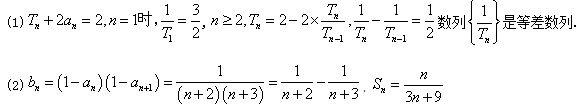 3.解:(1)设等比数列{an}的公比为q,则T1=a1,T2=2a1+a2=a1(2+q).又T1=1,T2=4,∴a1=1,q=2.(2)由(1)知:a1=1,q=2,∴an=2n-1.∴Tn=n·1+(n-1)·2+…+2·2n-2+1·2n-1,①2Tn=n·2+(n-1)·22+…+2·2n-1+1·2n.②②-①得:Tn=-n+2+22+…+2n-1+2n=2n+1-(n+2). 4.解:
3.解:(1)设等比数列{an}的公比为q,则T1=a1,T2=2a1+a2=a1(2+q).又T1=1,T2=4,∴a1=1,q=2.(2)由(1)知:a1=1,q=2,∴an=2n-1.∴Tn=n·1+(n-1)·2+…+2·2n-2+1·2n-1,①2Tn=n·2+(n-1)·22+…+2·2n-1+1·2n.②②-①得:Tn=-n+2+22+…+2n-1+2n=2n+1-(n+2). 4.解: 5.(1)a1=1,a2=3,a3=7;(2)an=2n-1,Sn=2an-n=2n-1-n-2. 6.
5.(1)a1=1,a2=3,a3=7;(2)an=2n-1,Sn=2an-n=2n-1-n-2. 6. 7.解:
7.解: 8.
8.
相关试卷
这是一份高考数学一轮复习课时作业:34 数列求和与数列的综合应用 Word版含解析,共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份高考数学(理数)一轮复习检测卷:5.4《数列求和及综合应用》 (学生版),共4页。试卷主要包含了已知数列{an}等内容,欢迎下载使用。
这是一份高考数学(理数)一轮复习检测卷:5.4《数列求和及综合应用》 (教师版)











