


所属成套资源:九上数学北师第三章单元测试卷
- 九上数学北师第一章单元测试卷 试卷 0 次下载
- 九上数学北师第二章单元测试卷 试卷 0 次下载
- 九上数学北师第四章单元测试卷 试卷 0 次下载
- 九上数学北师第五章单元测试卷 试卷 0 次下载
- 九上数学北师第六章单元测试卷 试卷 0 次下载
九上数学北师第三章单元测试卷
展开这是一份九上数学北师第三章单元测试卷,共9页。
第三章 概率的进一步认识
![]() 时间:90分钟
时间:90分钟 ![]() 满分:100分
满分:100分
一、选择题(共8小题,每小题3分,共24分.每小题有四个选项,其中只有一个选项符合题意)
1.用频率估计概率,可以发现抛掷硬币“正面向上”的概率为0.5,那么掷一枚质地均匀的硬币10次,下列说法正确的是 ( )
A.每两次必有1次正面向上
B.可能有5次正面向上
C.必有5次正面向上
D.不可能有10次正面向上
2.[教材变式P 61练习](2021·辽宁阜新中考)小颖有两顶帽子,分别为红色和黑色,有三条围巾,分别为红色、黑色和白色,她随机拿出一顶帽子和一条围巾戴上,恰好为红色帽子和红色围巾的概率是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.(2023·山东济南历城区期末)一个不透明的袋子里装有白棋子、黑棋子共20个,这些棋子除颜色外都相同.小明从中随机摸出一颗棋子,记下颜色后放回,通过多次重复试验发现,摸出白棋子的频率稳定在0.6,则袋子中白棋子的个数最有可能是 ( )
A.5 B.8 C.12 D.15
4.(2023·安徽宿州期中)2023年冬奥会吉祥物为“冰墩墩”,冬残奥会吉祥物为“雪容融”.现有三张正面印有吉祥物的不透明卡片,卡片除正面图案不同外,其余均相同,其中两张正面印有“冰墩墩”图案,一张正面印有“雪容融”图案,将三张卡片正面向下洗匀,从中随机一次性抽取两张卡片,则抽出的两张卡片正面都印有“冰墩墩”图案的概率是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.(2021·重庆期末)一个不透明的袋子中装有3个白球,2个黑球,它们除颜色外都相同.将球摇匀后,从中随机摸出一个球,记下颜色后不放回,再随机摸出一个球.两次摸到的球颜色相同的概率是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.(2023·河南许昌一中月考)某市教委部门高度重视自然灾害中的安全教育,要求各级各类学校从认识安全警示标志入手开展安全教育活动.某数学兴趣小组准备了4张印有安全警示标志的卡片,正面图案如图所示,它们除此之外完全相同,把这4张卡片背面朝上洗匀,从中随机抽取两张卡片,则这两张卡片上的正面图案中有一张是轴对称图形的概率是 ( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.(2021·辽宁铁岭期末)若从1,2,3,4这四个数字中任选一个记为a,再从这四个数字中任选一个记为c,则关于x的一元二次方程ax2+4x+c=0没有实数根的概率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.(2023·江苏南京鼓楼区期中)如图是用画树状图的方法画出的某个试验的所有可能发生的结果,则这个试验不可能是( )
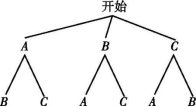
A.在一个不透明的袋中有3个除颜色外完全相同的小球,其中2个黑球,1个白球,从中随机取出2个球
B.小明,小王两个人分别去买一个盲盒,在三款盲盒中买到同一款盲盒
C.从某学习小组的两名男生和一名女生中随机选取两名学生进行竞答
D.体育测试中,随机从足球、篮球、排球三个项目中选择两个项目
二、填空题(共5小题,每小题4分,共20分)
9.(2023·北京期末)经过某个十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,那么甲汽车经过这个十字路口时,向右转的概率是 .
10.为积极响应“无偿献血,传递温暖”的号召,某高校一寝室的4个同学参与到爱心献血的活动中,他们其中有2个A型血,1个B型血,还有1个O型血,现从该寝室随机抽取2个同学参与第一批次献血,则2个同学都是A型血的概率为 .
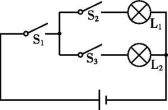
11.(2021·广东汕头潮阳区模拟)在如图所示的电路图中,随机闭合开关S1,S2,S3中的两个,能让灯泡L1发光的概率是 .
12.(2023·辽宁锦州期中)一张纸片上有一个不规则的图案,小雅想了解该图案的面积是多少,她采取了以下的试验办法:用一个长为5 cm,宽为3 cm的长方形,将不规则图案围起来如图(1)所示,然后在适当位置随机地向长方形区域扔小球,并记录小球落在不规则图案内的次数(球落在界线上或长方形区域外不计入试验结果),她将若干次有效试验的结果绘制成了图(2)所示的折线统计图,由此她估计此不规则图案的面积为 cm2.(结果保留整数)
 图(1)
图(1)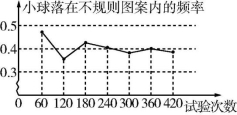 图(2)
图(2)
13.(2021·江苏镇江中考)一只不透明的袋子中装有1个黄球,现放若干个红球进去,它们与黄球除颜色外都相同,搅匀后从中任意摸出两个球,若使得P(摸出一红一黄)=P(摸出两红),则放入的红球个数为 .
三、解答题(共6小题,共56分)
14.(8分)近几年,各式各样的共享经济模式在各个领域迅速普及应用,如图是某同学收集的四个共享经济领域的图标,将收集到的图标制成编号为A,B,C,D的四张卡片(除编号和内容外,其余完全相同),背面朝上,洗匀放好.
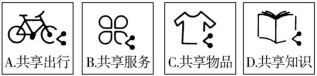
(1)从中随机抽取一张,抽到的卡片上的图标恰好是“共享知识”的概率为 ;
(2)从中随机抽取一张卡片,放回后洗匀,再从中随机抽取一张卡片,请用列表或画树状图的方法求抽到的两张卡片上的图标恰好是“共享出行”和“共享知识”的概率.
15.(8分)某商场在“五一”促销活动中规定,顾客每消费100元就能获得一次抽奖机会.为了活跃气氛,设计了两种抽奖方案.
方案一:转动转盘A一次,指针指向红的部分可领取一份奖品.
方案二:转动转盘B两次,两次指针都指向红的部分可领取一份奖品.
(两个转盘都被平均分成3份,若指针指向分界线,则重转)
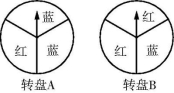
(1)转动一次转盘A,获得奖品的概率是 ;
(2)如果你获得一次抽奖机会,你会选择哪种方案?请用列表法或画树状图法说明理由.
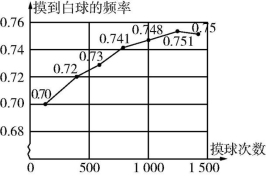
16.(9分)(2023·辽宁抚顺新抚区期末)一个黑箱子里装有红、白两种颜色的球共4只,它们除颜色外,其他都相同.小明将球搅匀后从箱子中随机摸出一个球,记下颜色,再把它放回,不断重复试验,根据多次试验结果画出如下的折线统计图.
(1)当试验次数很大时,摸到白球的频率将会接近 (精确到0.01),从箱子中摸一次球,摸到红球的概率是 ;
(2)从该箱子里随机摸出一个球,不放回,再摸出一个球.用画树状图法或列表法求摸到一个红球和一个白球的概率.
17.(10分)甲、乙、丙、丁四名同学进行一次乒乓球单打比赛,要从中选两位同学打第一场比赛.
(1)请用画树状图法或列表法求出恰好选中甲、乙两位同学的概率;
(2)请利用若干个除颜色外其他都相同的球,设计一个摸球试验(至少摸两次),并根据该试验写出一个发生概率与(1)中所求概率相同的事件.
18.(10分)(2021·黑龙江大庆期中)如图(1),一枚质地均匀的正四面体骰子,它有四个面,每个面上分别以1,2,3,4标号;如图(2),等边三角形ABC的三个顶点处各有一个圆圈.明明和亮亮想玩跳圈游戏,游戏的规则为:游戏者从圈A起跳,每投掷一次骰子,骰子着地的一面点数是几,就沿着三角形的边逆时针方向连续跳跃几个边长.如:若第一次掷得点数为2,就逆时针连续跳2个边长,落到圈C;若第二次掷得点数为4,就从圈C继续逆时针连续跳4个边长,落到圈A.
(1)明明随机掷一次骰子,她跳跃后落到圈A的概率为 ;
(2)明明和亮亮一起玩跳圈游戏:明明随机投掷一次骰子,亮亮随机投掷两次骰子,以最终落到圈A为胜者.这个游戏公平吗?请说明理由.
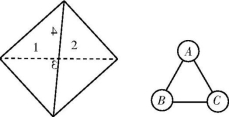
图(1) 图(2)
19.(11分)(2021·辽宁本溪期末)为了解学生对食品安全知识的了解情况,学校随机抽取了部分学生进行问卷调查,将调查结果按照“A:非常了解,B:了解,C:了解较少,D:不了解”四类分别进行统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
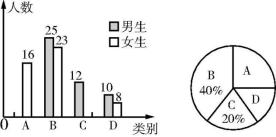
(1)此次共调查了 名学生;扇形统计图中D所在扇形的圆心角为 ;
(2)将上面的条形统计图补充完整;
(3)若该校共有800名学生,请你估计对食品安全知识“非常了解”的学生的人数;
(4)现有“非常了解”的男生2名,女生2名,从这4名学生中随机抽取2名学生进行座谈,刚好抽到同性别学生的概率是多少?
第三章 概率的进一步认识
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
B | D | C | A | B | A | C | B |
9. | 10. | 11. | |||||
12.6 | 13.3 | ||||||
16.(1)0.75 ![]() (4分)
(4分)
解法提示:由折线统计图可知,当试验次数很大时,摸到白球的频率将会接近0.75,从箱子中摸一次球,摸到红球的概率为1-0.75=0.25=![]() .
.
(2)由(1)知,箱中白球的个数为4×0.75=3,则红球的个数为4-3=1,列表如下:
| 白 | 白 | 白 | 红 |
白 |
| (白,白) | (白,白) | (红,白) |
白 | (白,白) |
| (白,白) | (红,白) |
白 | (白,白) | (白,白) |
| (红,白) |
红 | (白,红) | (白,红) | (白,红) |
|
由表知,共有12种等可能的结果,其中摸到一个红球和一个白球的结果有6种,
∴摸到一个红球和一个白球的概率为![]() =
=![]() . (9分)
. (9分)
17.(1)根据题意,画树状图如下:
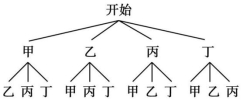 (3分)
(3分)
由树状图,可知共有12种等可能的结果,其中恰好选中甲、乙两位同学的结果有2种,
所以P(恰好选中甲、乙两位同学)=![]() =
=![]() . (5分)
. (5分)
(2)答案不唯一.如:在一个不透明的袋子中,放入四个除颜色外其他都相同的球,它们的颜色分别为白、黄、粉、橙,从袋中随机摸出一个球记下颜色,不放回,再从袋中随机摸出一个球,记下颜色.
事件:两次摸出的球一个是白球,一个是粉球. (10分)
18.(1)![]() (3分)
(3分)
(2)这个游戏不公平. (4分)
理由:画树状图如图,
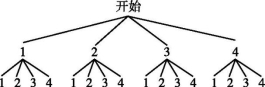
共有16种等可能的结果,其中亮亮随机投掷两次骰子,最终落到圈A的结果数为5,即共跳3个边长或6个边长,
所以P(亮亮随机投掷两次骰子,最终落回到圈A)=![]() . (8分)
. (8分)
因为![]() <
<![]() ,
,
所以这个游戏不公平. (10分)
19.(1)120 54° (2分)
(2)D所占的百分比为(10+8)÷120×100%=15%,
A中的人数为120×(1-40%-20%-15%)=30(名),其中男生有30-16=14(名),
C中的人数为120×20%=24(名),其中女生有24-12=12(名).
补全条形统计图如图所示: (4分)
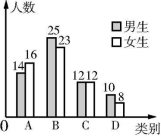
(3)800×(1-40%-20%-15%)=200(名),
答:估计对食品安全知识“非常了解”的学生的人数为200. (7分)
(4)画树状图:
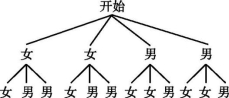
由树状图可知,共有12种等可能的结果,抽到同性别学生的结果有4种,
所以P(刚好抽到同性别学生)=![]() =
=![]() . (11分)
. (11分)









