华师大版八年级上册第13章 全等三角形13.2 三角形全等的判定4 角边角作业ppt课件

这是一份华师大版八年级上册第13章 全等三角形13.2 三角形全等的判定4 角边角作业ppt课件，共21页。

1. 下列选项中能判定△ABC≌△DEF的是(　　)A.AB=DE,BC=EF,∠A=∠DB.AB=DE,BC=EF,∠C=∠EC.∠A=∠D,AB=EF,∠B=∠ED.∠A=∠D,AB=DE,∠B=∠E
知识点1 判定两三角形全等的基本事实:角边角
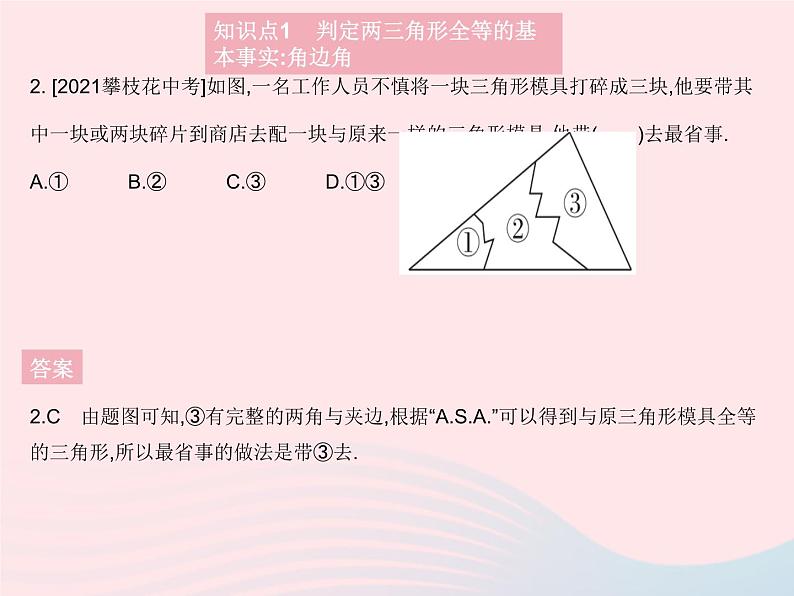
2. [2021攀枝花中考]如图,一名工作人员不慎将一块三角形模具打碎成三块,他要带其中一块或两块碎片到商店去配一块与原来一样的三角形模具,他带(　　)去最省事.A.①　　　B.②　　　C.③　　　D.①③
2.C　由题图可知,③有完整的两角与夹边,根据“”可以得到与原三角形模具全等的三角形,所以最省事的做法是带③去.
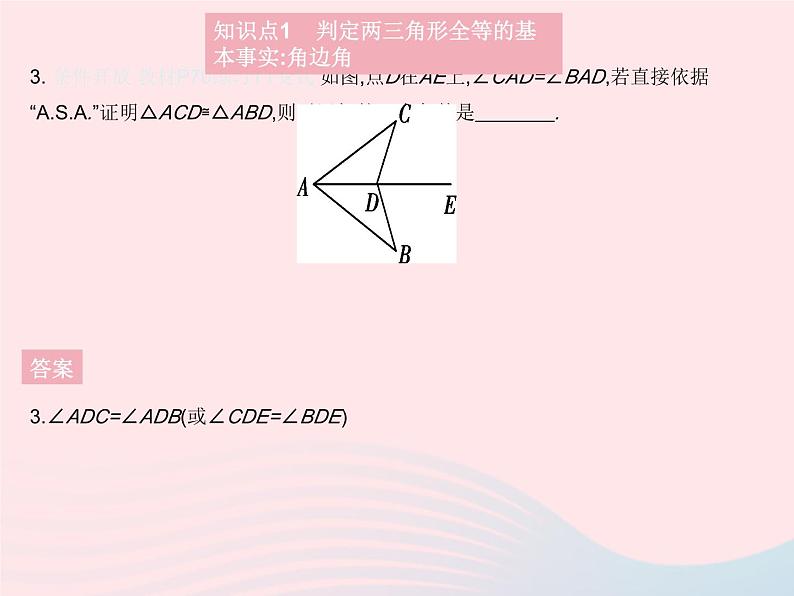
3. 条件开放 教材P70练习T1变式 如图,点D在AE上,∠CAD=∠BAD,若直接依据“”证明△ACD≌△ABD,则需添加的一个条件是　　　　. 
3.∠ADC=∠ADB(或∠CDE=∠BDE)
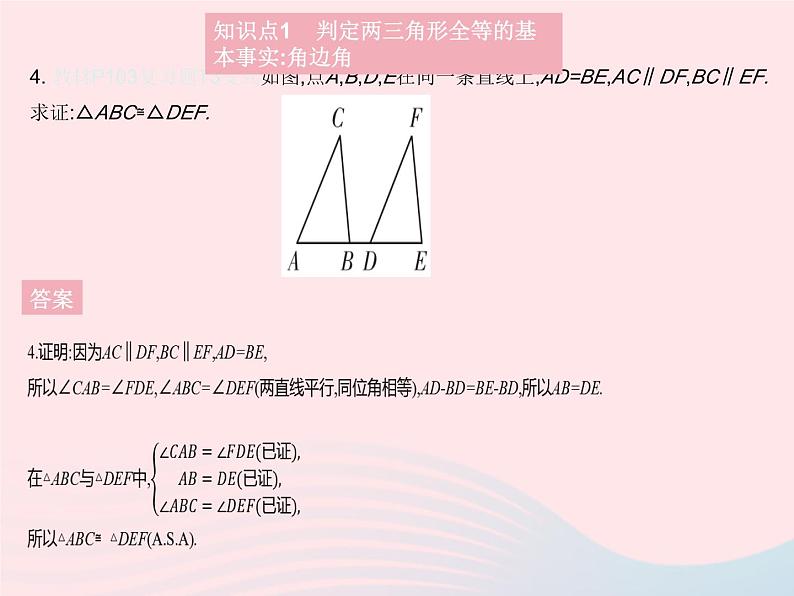
4. 教材P103复习题T3变式如图,点A,B,D,E在同一条直线上,AD=BE,AC∥DF,BC∥EF.求证:△ABC≌△DEF.
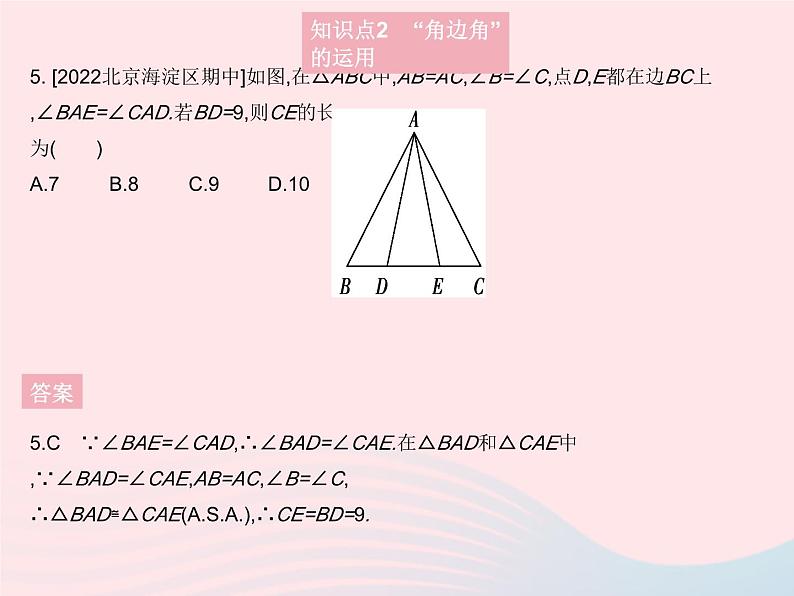
5. [2022北京海淀区期中]如图,在△ABC中,AB=AC,∠B=∠C,点D,E都在边BC上,∠BAE=∠CAD.若BD=9,则CE的长为(　　)A.7B.8C.9D.10
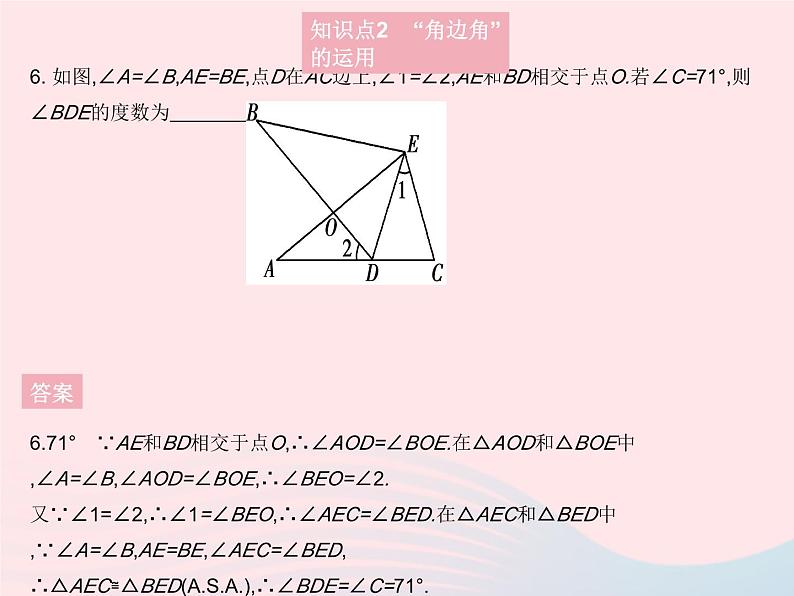
知识点2 “角边角”的运用
5.C　∵∠BAE=∠CAD,∴∠BAD=∠CAE.在△BAD和△CAE中,∵∠BAD=∠CAE,AB=AC,∠B=∠C,∴△BAD≌△CAE(),∴CE=BD=9.
6. 如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.若∠C=71°,则∠BDE的度数为　　　　. 
6.71°　∵AE和BD相交于点O,∴∠AOD=∠BOE.在△AOD和△BOE中,∠A=∠B,∠AOD=∠BOE,∴∠BEO=∠2.又∵∠1=∠2,∴∠1=∠BEO,∴∠AEC=∠BED.在△AEC和△BED中,∵∠A=∠B,AE=BE,∠AEC=∠BED,∴△AEC≌△BED(),∴∠BDE=∠C=71°.
7. [2022防城港期末]如图,已知点B,E,C,F在一条直线上,AC∥DE,AC=DE,∠A=∠D.求证:AB=DF.
7.证明:∵AC∥DE,∴∠ACB=∠DEF(两直线平行,内错角相等).在△ABC和△DFE中,∵∠A=∠D(已知),AC=DE(已知),∠ACB=∠DEF(已证),∴△ABC≌△DFE(),∴AB=DF(全等三角形的对应边相等).
8. [2020黄石中考]如图,AB=AE,AB∥DE,∠DAB=70°,∠E=40°.(1)求∠DAE的度数;(2)若∠B=30°,求证:AD=BC.
8.(1)解:∵AB∥DE(已知),∴∠EAB=∠E=40°(两直线平行,内错角相等),∵∠DAB=70°(已知),∴∠DAE=∠DAB-∠EAB=30°.(2)证明:在△BCA与△ADE中,∵∠B=∠DAE,AB=EA(已知),∠BAC=∠E(已证),∴△BCA≌△ADE(),∴AD=BC(全等三角形的对应边相等).
1. [2022龙岩期中]有一张三角形纸片ABC,已知∠B=∠C=x°,将三角形纸片按下列方式用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是(　　)
1.C　A项与B项,均可由“”证得两个小三角形全等;C项,如图1,∵∠DEC=∠B+∠BDE,∴x°+∠FEC=x°+∠BDE,∴∠FEC=∠BDE,∴BE和CF是对应边,而已知给的是BD=FC=3,无法判断BE与CF的数量关系,∴不能判定两个小三角形全等; D项,如图2,∵∠DEC=∠B+∠BDE,∴x°+∠FEC=x°+∠BDE,∴∠FEC=∠BDE.在△BDE与△CEF中,∵∠BDE=∠CEF,BD=CE=2,∠B=∠C,∴△BDE≌△CEF(),∴能判定两个小三角形全等.综上,可能得不到全等三角形纸片的是选项C.
2. [2021内江期末]如图,△ABC的面积为16,AD平分∠BAC,且AD⊥BD于点D,则△ADC的面积是(　　)A.6B.8C.10D.12
3. [2022台州期中]如图,在△ABC中,AB=AC,∠B=∠ACD=45°,D,E是BC上两点,且∠DAE=45°,过点A作AF⊥AD,垂足是A,过点C作CF⊥BC,垂足是C,CF交AF于点F,连接EF.给出下列结论:①△ABD≌△ACF;②DE=EF;③若S△ADE=10,S△CEF=4,则S△ABC=24;④BD+CE=DE.其中正确结论的序号是　　　　. 
3.①②③ ∵∠B=∠ACB=45°,∴∠BAC=90°.∵AF⊥AD,BC⊥CF,∴∠DAF=∠BAC=∠ECF=90°,∴∠BAD=∠CAF,∠B=∠ACF=45°,又∵AB=AC,∴△ABD≌△ACF(),故①正确.∵△ABD≌△ACF,∴AD=AF.∵AE=AE,∠EAD=∠EAF=45°,AD=AF,∴△AED≌△AEF(),∴DE=EF,故②正确.∵S△ADE=10,S△CEF=4,∴S四边形AECF=S△ACF+S△AEC=S△ABD+S△AEC=S△AEF+S△CEF=S△ADE+S△CEF=14,∴S△ABC=S△ABD+S△AEC+S△ADE=14+10=24,故③正确.∵△ABD≌△ACF,∴BD=CF.∵EC+CF>EF,∴BD+CE>DE,故④错误.故正确结论的序号是①②③.
4. 点D在△ABC的边BA的延长线上,点F在边BC的延长线上,点E在平面内,∠E=∠BDC,AE=CD,∠EAB+∠DCF=180°.(1)如图1,求证:AD+BC=BE.(2)如图2、图3,请分别写出线段AD,BC,BE之间的数量关系,不需要证明.
素养提升5. 观察发现:如图1,OP平分∠MON,在OM,ON上分别取点A,B,使OA=OB,再在OP上任取一点D,连接AD,BD,请你猜想AD与BD之间的数量关系,并说明理由.拓展应用:如图2,在△ABC中,∠ACB=90°,∠B=60°,AD,CE分别平分∠BAC,∠BCA,AD,CE相交于点F,请你写出FE与FD之间的数量关系,并说明理由.
5.解:观察发现:AD=BD.理由如下:∵OP平分∠MON,∴∠DOA=∠DOB.在△OAD和△OBD中,∵OA=OB,∠DOA=∠DOB,OD=OD,∴△OAD≌△OBD(),∴AD=DB.拓展应用:FE=FD.理由如下:如图,在AC上截取AG=AE,连接FG.∵AD平分∠BAC,∴∠EAF=∠GAF.在△AEF和△AGF中,∵AE=AG,∠EAF=∠GAF,AF=AF,∴△AEF≌△AGF(),∴∠AFE=∠AFG,FE=FG.∵∠ACB=90°,∠B=60°,∴∠BAC=30°.∵AD,CE分别平分∠BAC,∠BCA,