华师大版八年级上册3 边角边教学ppt课件

这是一份华师大版八年级上册3 边角边教学ppt课件，共23页。PPT课件主要包含了SAS，不一定，∠AOD＝∠BOC，OD＝OC，SSA，不全等于，钝角三角形，①②③等内容，欢迎下载使用。

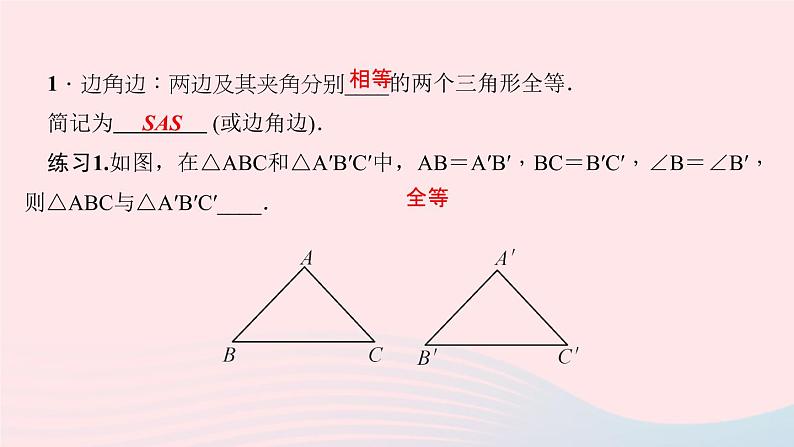
1．边角边：两边及其夹角分别____的两个三角形全等．简记为 (或边角边)．练习1.如图，在△ABC和△A′B′C′中，AB＝A′B′，BC＝B′C′，∠B＝∠B′，则△ABC与△A′B′C′____．
2．两边和其中一边的对角对应相等的两个三角形 全等．练习2.△ABC和△A′B′C′中，若AB＝A′B′，BC＝B′C′，∠C＝∠C′，则△ABC与△A′B′C′ 全等．(填“一定”“不一定”或“不能”)
1．在△ABC和△DEF中，下列给出的条件，能用“”判定△ABC≌△DEF的是(　　)A．AB＝DE，∠A＝∠D，BC＝EFB．AB＝EF，∠A＝∠D，AC＝DFC．AB＝BC，∠B＝∠E，DE＝EFD．BC＝EF，∠C＝∠F，AC＝DF
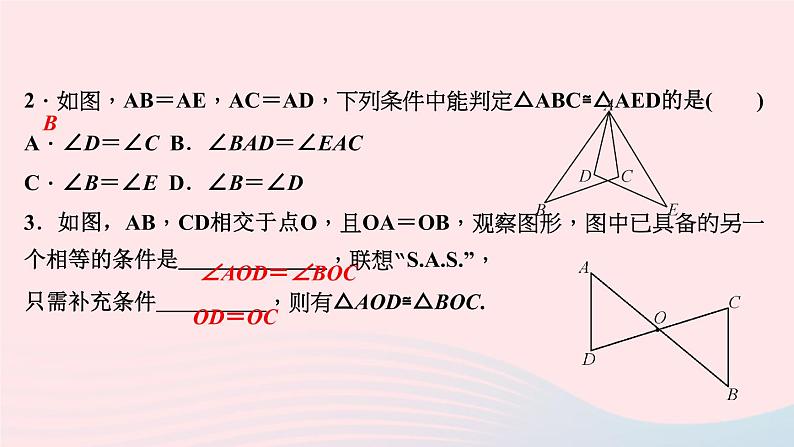
2．如图，AB＝AE，AC＝AD，下列条件中能判定△ABC≌△AED的是(　　)A．∠D＝∠C B．∠BAD＝∠EACC．∠B＝∠E D．∠B＝∠D3．如图，AB，CD相交于点O，且OA＝OB，观察图形，图中已具备的另一个相等的条件是 ，联想“”，只需补充条件 ，则有△AOD≌△BOC.
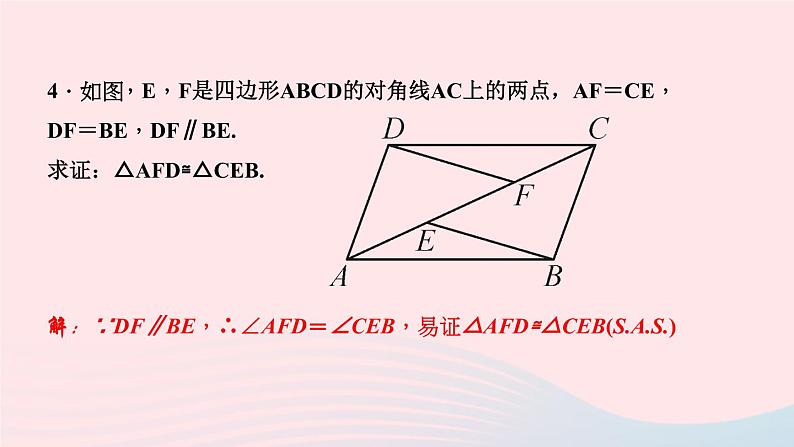
4．如图，E，F是四边形ABCD的对角线AC上的两点，AF＝CE，DF＝BE，DF∥BE.求证：△AFD≌△CEB.解：∵DF∥BE，∴∠AFD＝∠CEB，易证△AFD≌△CEB()
5．如图，将两根钢条AA′，BB′的中点O连结在一起，使AA′，BB′可以绕着O自由转动，做成一个测量工件，则AB的长等于内槽宽A′B′，那么判定△OAB≌△OA′B′的理由是(　　)A．边角边 B．角边角C．边边边 D．角角边
6．小红用同种材料制成的金属框架如图所示，已知∠B＝∠E，AB＝DE，BF＝EC，其中△ABC的周长为24 cm，CF＝3 cm，则制成整个金属框架所需这种材料的长度为(　　)A．51 cm B．48 cmC．45 cm D．54 cm
7．下面是胡老师带领学生，探究“”是否能判定两个三角形全等的过程，填空：如图，已知CD＝CB，在△ABC和△ADC中，AC＝____(公共边)，CB＝CD(已知)，∠A＝∠A(公共角)，则△ABC和△ADC满足两边及一边的对角分别相等，即满足____，很显然，△ABC △ADC(填“全等于”或“不全等于”)，从而得出结论：(填“能”或“不能”)判定两个三角形全等．
8．如图，AD＝AE，BE＝CD，∠1＝∠2＝110°，∠BAE＝60°，那么∠CAE等于(　　)A．20° B．30° C．40° D．50°
9．(六盘水中考)我们知道“两边及其中一边的对角分别相等的两个三角形不一定全等”，但是，小亮发现：当这两个三角形都是锐角三角形时，它们会全等，除小亮的发现之外，当这两个三角形都是 时，它们也会全等；当这两个三角形其中一个三角形是锐角三角形，另一个是 时，它们一定不全等．
钝角三角形或直角三角形
10．(南京中考)如图，四边形ABCD的对角线AC，BD相交于点O，△ABO≌△ADO.下列结论：①AC⊥BD；②CB＝CD；③△ABC≌△ADC；④DA＝DC.其中所有正确结论的序号是 ．
11．(宁德中考)如图，在△ABC和△DAE中，D是AC上一点，AD＝AB，DE∥AB，DE＝AC.求证：AE＝BC.解：易证△ADE≌△BAC()，∴AE＝BC
12．(曲靖中考)如图，点B，E，C，F在一条直线上，AB＝DF，AC＝DE，∠A＝∠D.(1)求证：AC∥DE；解：易证△ABC≌△DFE()，∴∠ACE＝∠DEF，∴AC∥DE
13．如图，四边形ABCD是正方形，BE⊥BF，BE＝BF，EF与BC交于点G.(1)求证：AE＝CF；(2)若∠ABE＝55°，求∠EGC的度数．
解：(1)∵四边形ABCD是正方形，∴∠ABC＝90°，AB＝BC，∴∠ABE＋∠EBC＝90°，∵BE⊥BF，∴∠FBE＝90°，∴∠CBF＋∠EBC＝90°，∴∠ABE＝∠CBF，易证△ABE≌△CBF()，∴AE＝CF　(2)∵BE⊥BF，∴∠FBE＝90°，又∵BE＝BF，∴∠BEF＝∠BFE＝45°，∵四边形ABCD是正方形，∴∠ABC＝90°，又∵∠ABE＝55°，∴∠EBG＝90°－55°＝35°，∴∠EGC＝∠EBG＋∠BEF＝35°＋45°＝80°
14．(阿凡题　1072029)两个大小不相同的等腰直角三角板如图①放置，图②是由它抽象出的几何图形，B，C，E在同一条直线上，连结DC.(1)请找出图②中的全等三角形并给予证明；(说明：结论中不得含有未标识的字母)(2)求证：DC⊥BE.