





初中数学华师大版八年级上册4 角边角习题课件ppt
展开对边;∠A′;∠B′;BC
两角分别相等且其中一组等角的________相等的两个三角形全等.简记为(或角角边).其书写模式为:∴△ABC≌△A′B′C′.
1.如图,∠B=∠C,AB=DC.证明△ABO≌△DCO,应首先选择的判定方法为( ) A. B. C. D.无法证明
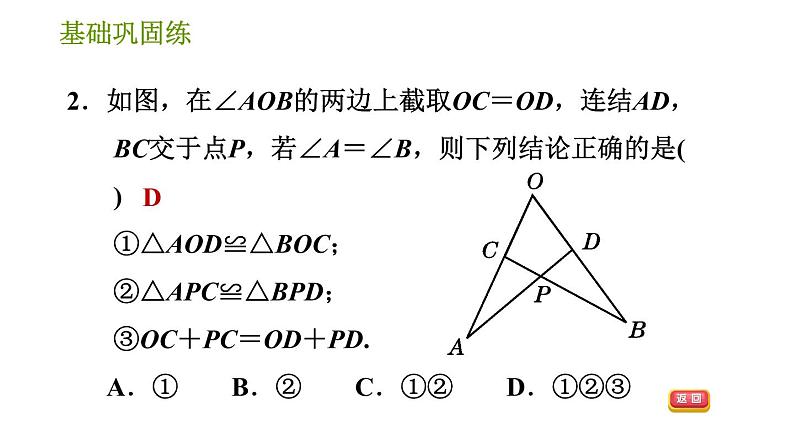
2.如图,在∠AOB的两边上截取OC=OD,连结AD,BC交于点P,若∠A=∠B,则下列结论正确的是( )①△AOD≌△BOC;②△APC≌△BPD;③OC+PC=OD+PD. A.① B.② C.①② D.①②③
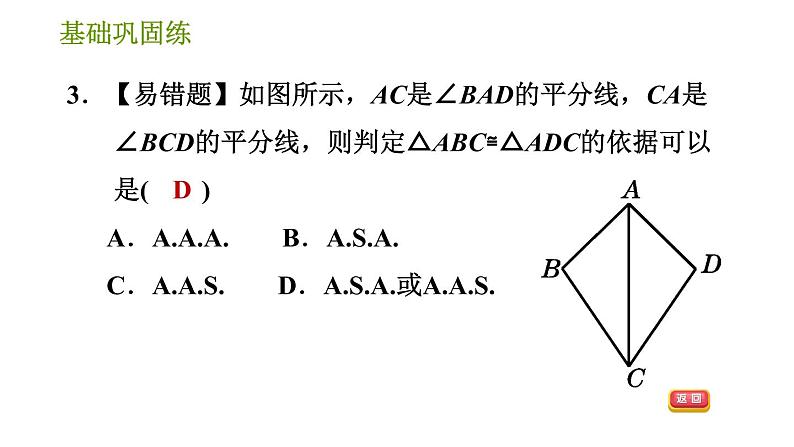
3.【易错题】如图所示,AC是∠BAD的平分线,CA是∠BCD的平分线,则判定△ABC≌△ADC的依据可以是( ) A. B. C. D.或
4.【2021·武汉期末】如图,已知∠BCA=∠DCA,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( ) A.AB=AD B.∠BAC=∠DAC C.CB=CD D.∠B=∠D=90°
5.如图,已知AB∥CF,点E为DF的中点,若AB=9 cm.CF=5 cm,则BD=( ) A.5 cm B.4 cm C.2.5 cm D.4.5 cm
6.【中考·深圳】如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,添加下列哪一个条件后仍无法证明△ABC≌△DEF?( ) A.AC∥DF B.∠A=∠D C.AC=DF D.∠ACB=∠F
7.如图,∠1=∠2,∠C=∠D,AC,BD相交于点E,下列结论不正确的是( ) A.∠DAE=∠CBE B.△DEA与△CEB不全等 C.CE=DE D.△AEB是等腰三角形
8.如图,∠1=∠2,∠3=∠4,OE=OF,则图中全等的三角形共有( ) A.1对 B.2对 C.3对 D.4对
【点拨】由已知可判定△OEB≌△OFA,∴OA=OB,从而AE=BF,∴△AEC≌△BFC,故B正确.
9.如图,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B,D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为________.
10.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为点E,AB=12 cm,则△DEB的周长为________cm.
11.【2021·柳州期末】如图,AD⊥BC,垂足为D,BF⊥AC,垂足为F,AD与BF交于点E,AD=BD=5,DC=2,则AE的长为( ) A.2 B.5 C.3 D.7
12.【中考·葫芦岛】如图,在△ABC中,∠B=∠C,D为BC的中点,过D分别向AB,AC作垂线段,则能够直接判断△BDE≌△CDF的理由是________.
【点拨】∵∠BED=∠CFD=90°,∠B=∠C,D是BC的中点,∴BD=CD,故根据可证明△BDE≌△CDF.
13.【2020·昆明】如图,AC平分∠BAE,点D是线段AC上的一点,∠C=∠E,AB=AD.求证:BC=DE.
证明:∵AC平分∠BAE,∴∠BAC=∠DAE.又∵∠C=∠E,AB=AD,∴△BAC≌△DAE(),∴BC=DE.
14.【中考·温州】如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F.(1)求证:△BDE≌△CDF;
证明:∵CF∥AB,∴∠B=∠FCD,∠BED=∠F.∵AD是BC边上的中线,∴BD=CD,∴△BDE≌△CDF.
(2)当AD⊥BC,AE=1,CF=2时,求AC的长 .
解:∵△BDE≌△CDF,∴BE=CF=2,∴AB=AE+BE=1+2=3.∵AD⊥BC,BD=CD,∴AC=AB=3.
15.【2021·驻马店期末】证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程.下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图, ∠AOC=∠BOC,点P在OC上,____________________________________________.求证:________.请你补全已知和求证,并写出证明过程.
PD⊥OA,PE⊥OB,垂足分别为D,E
16.【中考·长春】感知:如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知:DB=DC.探究:如图②,AD平分∠BAC,∠B+∠ACD=180°,∠B<90°,求证:DB=DC.
初中数学华师大版八年级上册4 角边角评课ppt课件: 这是一份初中数学华师大版八年级上册4 角边角评课ppt课件,共20页。PPT课件主要包含了两角一边,画一画,说理验证,BC=CB公共边,∠C=∠C公共角,∴∠C∠C1,判定定理,巩固练习,边角边,角边角等内容,欢迎下载使用。
华师大版八年级上册第13章 全等三角形13.2 三角形全等的判定4 角边角说课ppt课件: 这是一份华师大版八年级上册第13章 全等三角形13.2 三角形全等的判定4 角边角说课ppt课件,共20页。PPT课件主要包含了ABAB,ACAD,∠CAB∠DAB,BCBD,∠CBA∠DBA,都全等,角边角公理,用符号语言表达为,课堂练习,∠AEC∠BFD等内容,欢迎下载使用。
华师大版八年级上册第13章 全等三角形13.2 三角形全等的判定4 角边角图文课件ppt: 这是一份华师大版八年级上册第13章 全等三角形13.2 三角形全等的判定4 角边角图文课件ppt,共18页。PPT课件主要包含了SAS,角边角,角角边,都全等,“角边角”判定方法,几何语言,“角角边”判定方法,∠B∠E,或∠A∠D,或ACDF等内容,欢迎下载使用。














