
初中数学北师大版九年级下册1 圆教学设计
展开正多边形的面积计算
我们知道,正四边形(正方形)面积等于,正三角形的面积等于。我不禁想到了:那么正五边形、正六边形呢?通过画图计算,我发现正六边形的面积公式比较容易推导,而正五边形的则复杂一些。
如图是一个边长为a的正六边形。连接AC,DF,过B作BG⊥AC。BG=,AC=。=ACBG=。==。
用类似的方法,我求得了正五边形的面积公式,不过结果十分复杂。我求得。我想化简这个结果。通过观察公式,我发现可以将化简为,即。得到这个结果,我挺满意,又考虑能不能把也变成与有关的形式。经过尝试,我进行了以下变形:,而又有,所以。所以。。而利用黄金三角形,可以求得。虽然这是根式的形式,但是代入原式会异常复杂,还不如三角函数的表示形式简明。
我又想有没有能够适用于所有正多边形的公式,而不用屡次尝试化简三角函数。
很快,我找到了一个普遍适用的新方法。作出该正多边形的中心O,连接OB,OC,过O作OE⊥BC。设该正多边形为正n边形,边长为a。OB=OC,∠BOC=,BE=CE=,∠BOE=。OE== 。==。发现了这个结论,我很高兴,将n=3,n=4,n=6逐一带入,都与之前的结果相符。
这时,我又联想到了圆。圆可以看成正无数边形,那么圆的面积公式=与这个公式是否统一呢?我发现将边心距OE=记为h,那么a=。将其代入=得到=。将这个公式与=类比,可得当正n边形变数无限大时,就无限接近于。不过似乎不能化简而我又想到了,前面我用OE来近似表示半径,那如果用OB来表示呢?同样,我求得OB=,记OB=h’,a=’。代入得=。同上,当正n边形变数无限大时,也无限接近于。当与无限接近时,即有,又,近似等于1,即n无穷大。这说明了该结论的正确性。
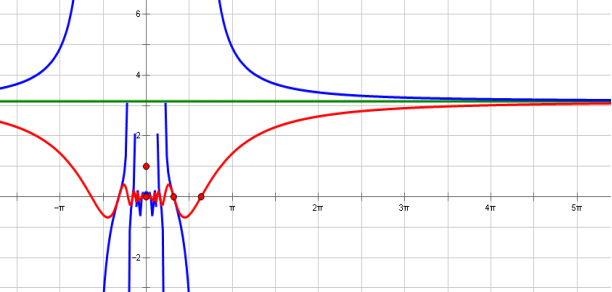
由图像可以看出,函数值无限接近
初中数学人教版九年级上册24.1.1 圆教案: 这是一份初中数学人教版九年级上册24.1.1 圆教案,共5页。教案主要包含了学生起点分析,教学任务分析,教学设计分析,教学设计反思等内容,欢迎下载使用。
人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.1 圆教案: 这是一份人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.1 圆教案,共5页。教案主要包含了学生起点分析,教学任务分析,教学设计分析,教学设计反思等内容,欢迎下载使用。
九年级上册24.1.1 圆教学设计: 这是一份九年级上册24.1.1 圆教学设计,共4页。教案主要包含了知识回顾,情景导入,新知探究,课堂检测,谈谈本节课的收获,作业等内容,欢迎下载使用。













