数学九年级下册1 圆导学案

第三章　　圆

3.4 圆周角和圆心角的关系（第2课时）

一、学习准备

 活动一：  学习准备

1.求图中角X的度数：

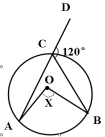
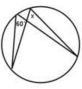
x=                     x=                     x=        

   二、探索新知

活动二：探究圆周角定理的推论

（1）在图3-17中，BC是⊙O的直径，它所对的圆周角有什么特点？你能证明你的结论吗？

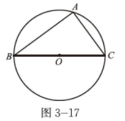
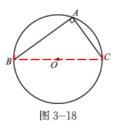
（2）在图3-18中，圆周角∠A=90°，弦BC是直径吗？为什么？

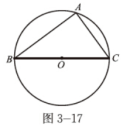
（3）从上面的两个议一议，得出推论：

  推论：

直径所对的圆周角是_________；90°的圆周角所对的弦是________.

  符号语言表示：                          

活动三：练习巩固

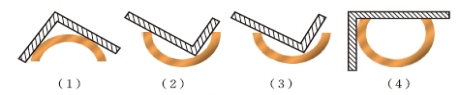
1、小明想用直角尺检查某些工件是否恰好为半圆形.下面所示的四种圆弧形，你能判断哪个是半圆形？为什么？

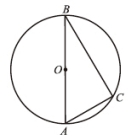
 2、如图，⊙O的直径AB=10cm，C为⊙O上的一点，∠B=30°，求AC的长.

                                                           活动四：究圆内接四边形的定义及性质

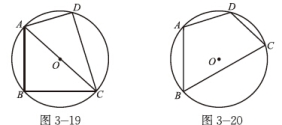
（1）在图3-19，图3-20，两个四边形ABCD有什么共同的特点？

圆内接四边形的定义：

________________，这样的四边形叫做圆内接四边形；这个圆叫做四边形的外接圆.

（2）如图3-19，四边形ABCD是⊙O的内接四边形，AC为⊙O的直径，请问∠BAD与∠BCD之间有什么关系？为什么？                      

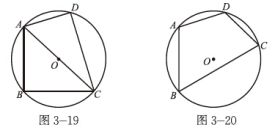
（3）如图3-20，C点的位置发生了变化，∠BAD与∠BCD之间有的关系还成立吗？为什么？                                       

（4）通过议一议环节，我们我们发现∠BAD与∠BCD之间有什么关系？

推论：

圆内接四边形的对角__________.

符号语言：

活动五：例题解析

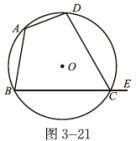例  如图3-21，∠DCE是圆内接四边形ABCD的一个外角，∠A与∠DCE的大小有什么关系？

活动六：议一议

议一议：在得出本节结论的过程中，你用到了哪些方法？请举例说明，并与同伴进行交流.

练习巩固

1、在圆内接四边形ABCD中，∠A与∠C的度数之比为4:5，求∠C的度数.

2、如图，在⊙O中，∠BOD=80°，求∠A和∠C的度数.

四、小结：

通过本节课的学习，你学到了哪些知识？