初中数学北师大版九年级下册1 圆教学设计

这是一份初中数学北师大版九年级下册1 圆教学设计，共7页。
第三章  圆直线和圆的位置关系（第2课时）教学设计一、              学生起点分析学生的知识技能基础：之前的课程学生已经学习了与圆有关的概念，如半径、圆周角、圆心角等，学习了圆的性质，学习了直线和圆的三种位置关系，这里将进一步讨论其中的一种情况：相切。学生的活动经验基础：进入初三下学期的学生在观察、操作、猜想能力较强，但逻辑推理、归纳、运用数学意识的思想比较薄弱，思维的广阔性、敏捷性、结密性、灵活性比较欠缺，自主探究和合作学习能力也需要在课堂教学中进一步加强和引导。学生思维活跃，能跟上教师的思路，并用完整的话回答老师的提问;但学生课堂回答问题的气氛不是那么浓厚，学习不具有自觉性，需要教师设计好教学环节，并给予充分的关注和指导。二、              教学任务分析本节课的内容是北师大九年级初中下册数学第三章《圆》第六节《直线和圆的位置关系》的第二课时。具体的教学目标为：知识与技能（1）能判定一条直线是否为圆的切线．（2）会过圆上一点画圆的切线．（3）会作三角形的内切圆． 过程与方法（1）通过判定一条直线是否为圆的切线，训练学生的推理判断能力．（2）会过圆上一点画圆的切线，训练学生的作图能力． 情感态度与价值观（1）经历观察、实验、猜想、证明等数学活动过程，发展合情推理能力和初步演绎推理能力，能有条理地、清晰地阐述自己的观点．（2）经历探究圆与直线的位置关系的过程，掌握图形的基础知识和基本技能，并能解决简单的问题．教学重点（1）探索圆的切线的判定方法，并能运用．（2）作三角形内切圆的方法．教学难点    探索圆的切线的判定方法． 三、              教学过程分析    本节课设计了五个教学环节：引入新课、新课讲解、课堂练习、课时小结、布置作业。 第一环节  引入新课    上节课我们学习了直线和圆的位置关系，圆的切线的性质，懂得了直线和圆有三种位置关系：相离、相切、相交．判断直线和圆属于哪一种位置关系，可以从公共点的个数和圆心到直线的距离与半径作比较两种方法进行判断，还掌握了圆的切线的性质、圆的切线垂直于过切点的直径．    由上可知，判断直线和圆相切的方法有两种，是否仅此两种呢?本节课我们就继续探索切线的判定条件． 第二环节  新课讲解活动内容：1．探索切线的判定条件2．做一做3．如何作三角形的内切圆4．补充例题讲解     1．探索切线的判定条件    如下图，AB是⊙O的直径，直线l经过点A，l与AB的夹角为∠α，当l绕点A旋转时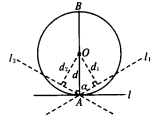，(1)随着∠α的变化，点O到l的距离(d如何变化?直线l与⊙O的位置关系如何变化?(2)当∠α等于多少度时，点O到l的距离d等于半径r?此时，直线l与⊙O有怎样的位置关系?为什么?实际教学效果：在教学中，教师可以引导学生，画一个圆，并画出直径AB，拿直尺当直线，让直尺绕着点A移动．观察∠α发生变化时，点O到l的距离d如何变化，然后互相交流意见．以下是实际教学中，学生得到的结论：    生1：如上图，直线l1与AB的夹角为α,点O到l的距离为d1，d1<r，这时直线l1与⊙O的位置关系是相交；当把直线l1沿顺时针方向旋转到l位置时，∠α由锐角变为直角，点O到l的距离为d，d=r，这时直线l与⊙O的位置关系是相切：当把直线l再继续旋转到l2位置时，∠α由直角变为钝角，点O到l的距离为d2，d2<r，这时直线l与⊙O的位置关系是相离．    生2：当∠α=90°时，点O到l的距离d等于半径．此时，直线l与⊙O的位置关系是相切，因为从上一节课可知，当圆心O到直线l的距离d＝r时，直线与⊙O相切．    生3：这就得出了判定圆的切线的又一种方法：经过直径的一端，并且垂直于这条直径的直线是圆的切线． 2．做一做    已知⊙O上有一点A，过A作出⊙O的切线．    分析：根据刚讨论过的圆的切线的第三个判定条件可知：经过直径的一端，并且垂直于直径的直线是圆的切线，而现在已知圆心O和圆上一点A，那么过A点的直径就可以作出来，再作直径的垂线即可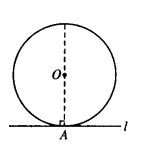．    如右图．    (1)连接OA．    (2)过点A作OA的垂线l，l即为所求的切线． 3．如何作三角形的内切圆．   如下图，从一块三角形材料中，能否剪下一个圆使其与各边都相切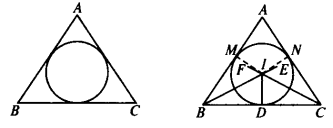．    分析：假设符号条件的圆已作出，则它的圆心到三角形三边的距离相等．因此，圆心在这个三角形三个角的平分线上，半径为圆心到三边的距离．    解：(1)作∠B、∠C的平分线BE和CF，交点为I(如右上图)．    (2)过I作ID⊥BC，垂足为D．    (3)以I为圆心，以ID为半径作⊙I．⊙I就是所求的圆．    ∵I在∠B的角平分线BE上，∴ID＝IM，又∵I在∠C的平分线CF上．∵ID＝IN，∵ID＝IM＝IN．这是根据角平分线的性质定理得出的，所以I到△ABC三边的距离相．等 因此和三角形三边都相切的圆可以作出一个，因为三角形三个内角的平分线交于一点，这点为圆心，这点到三角形三边的距离相等，这个距离为半径，圆心和半径都确定的圆只有一个．并且只能作出一个，这个圆叫做三角形的内切圆(inscribed circle of triangle)，内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心(incenter)． 4．（补充）例题讲解   如下图，AB是⊙O的直径，∠ABT=45°，AT＝AB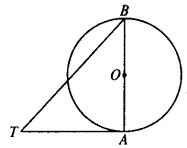．求证：AT是⊙O的切线．    分析：AT经过直径的一端，因此只要证AT垂直于AB即可，而由已知条件可知AT=AB，所以∠ABT＝∠ATB，又由∠ABT＝45°，所以∠ATB=45°．    由三角形内角和可证∠TAB=90°，即AT⊥AB．    证明：∵AB=AT，∠ABT＝45°．    ∴∠ATB＝∠ABT＝45°．    ∴∠TAB=180°-∠ABT-∠ATB=90°．∴AT⊥AB，即AT是⊙O的切线． 第三环节  课堂练习随堂练习1．以边长为3,4,5的三角形的三个顶点为圆心,分别作圆与对边相切,则这三个圆的半径分别是多少?2．分别作出锐角三角形,直角三角形,钝角三角形的内切圆,并说明与它们内心的位置情况?  第四环节  课时小结    本节课学习了以下内容：    1．探索切线的判定条件．    2．会经过圆上一点作圆的切线．    3．会作三角形的内切圆．    4．了解三角形的内切圆，三角形的内心概念． 第五环节  课后作业必做： 习题3.8     1,2题选做：已知AB是⊙O的直径，BC是⊙O的切线，切点为B，OC平行于弦AD．  求证：DC是⊙O的切线．  四、              教学反思1、运用课件创设最佳情境在课堂教学中营造一个宽松，和谐，民主的良好氛围。使师生，生生关系没有距离感，畏惧感，大家都无拘无束，学生才会全身心地投入到学习活动中。同时通过课件的演示，达到吸引学生的注意力、激发学生学习兴趣，减轻心理压力的目的。2、教给学法，实现自主合作学习自主发展，主要考虑学生的内在因素，新《数学课程标准（实验稿）》在前言部分--基本理念中有这样一句话：有效的数学学习活动不能单纯地依赖模仿与记忆，动手实践、自主探索与合作交流是学生数学学习的重要方式。从这句话我们可以看出，新课程标准不是对传统教学的完全摈弃，而是对传统教学中比较忽视的部分进行补充。比如模仿与记忆在我们的传统数学教学中比较注重，而今新课程标准中它仍旧是有效的数学学习活动，只是有动手实践、自主探索与合作交流等数学学习活动加以补充。因此在本节课教学中，坚持以学生为主，把课堂还给学生，让学生自主选学，自由组合，运用学法，合作探究，自主选择题目练习和表达方式。充分发挥学生自身的积极性，能动性，创造性，通过灵活运用多种教学策略，培养学生逻辑推理能力，突破本节课的重难点。课堂教学问题的设计，是教师传授知识与了解学生掌握知识程度的重要途径，是能否调动学生学习兴趣的重要手段，本节课我觉得自己所设计的问题在把握在新旧知识的衔接点上，在围绕教学内容的重难点上，从学生学习效果上看，似乎并不是那么完满。