第2章四边形2.2平行四边形习题课件（湘教版八下）

这是一份第2章四边形2.2平行四边形习题课件（湘教版八下），共13页。
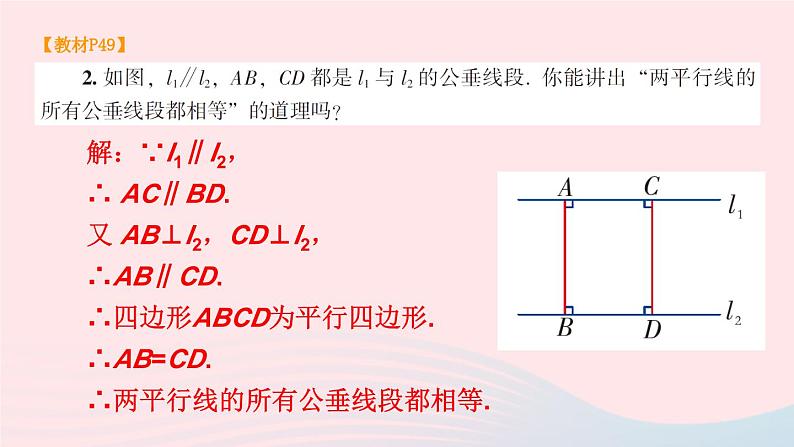
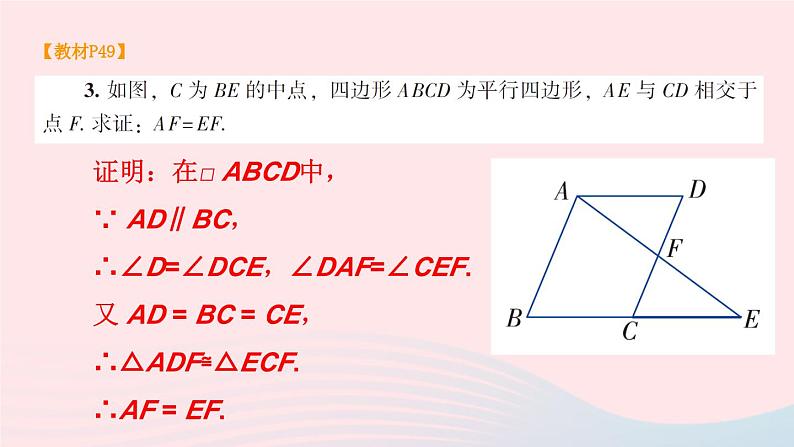
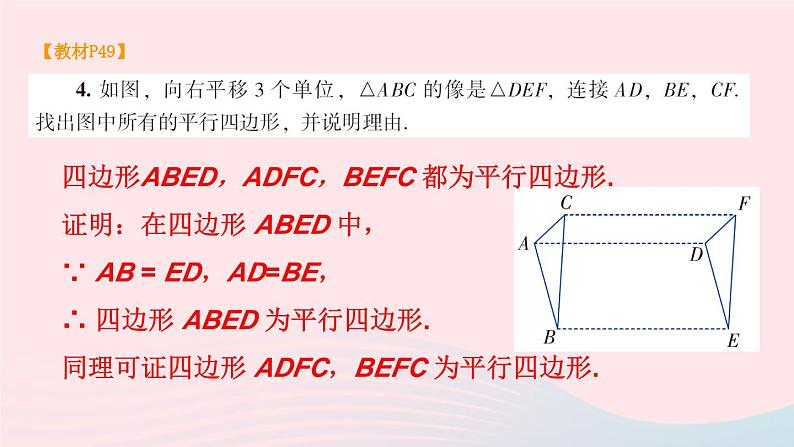
湘教·八年级下册【教材P49】有 9 个平行四边形.与 ∠A 相等的角有 ∠C，∠EMG，∠BHG，∠EFD，∠BEM，∠MGD，∠HMF.【教材P49】解：∵l1∥l2，∴ AC∥BD.又 AB⊥l2，CD⊥l2，∴AB∥CD.∴四边形ABCD为平行四边形.∴AB=CD.∴两平行线的所有公垂线段都相等.【教材P49】证明：在□ ABCD中，∵ AD∥BC，∴∠D=∠DCE，∠DAF=∠CEF.又 AD = BC = CE，∴△ADF≌△ECF.∴AF = EF.【教材P49】四边形ABED，ADFC，BEFC 都为平行四边形.证明：在四边形 ABED 中，∵ AB = ED，AD=BE，∴ 四边形 ABED 为平行四边形.同理可证四边形 ADFC，BEFC 为平行四边形.【教材P49】（1）四边形 ABDC 是平行四边形理由：∵ AC = AB = BD = DC，∴ 四边形 ABDC 是平行四边形.（2）不是.【教材P50】证明：连接 BD，交 AC 于点 O .∵ 四边形ABCD是平行四边形，∴OA=OC，OB=OD∵AE = CF ，∴ OE = OF.又 BD，EF是四边形 EBFD的对角线，∴ 四边形 ABDC 是平行四边形.O 【教材P50】□ ABCD 的面积为 24，可以证明图中红色部分与白色部分的面积相等，故红色部分的面积为 12.【教材P50】（1）四边形 ADEF，BEFD，CFDE 为平行四边形.证明：∵ DE∥AC，EF∥BA，∴DE∥AF，EF∥DA.∴四边形 ADEF是平行四边形.同理可证，四边形 BEFD，CFDE 为平行四边形.【教材P50】（2）∠DEF = ∠A，∠EFD=∠B，∠FDE=∠C.理由：四边形 ADEF，BEFD，CFDE 是平行四边形，平行四边形的对角相等.【教材P50】（3）证明：由（1）可知：AD=EF=BD，BE=DF=EC，AF=DE=FC .∴D, E, F 分别是 AB，BC，CA 的中点.【教材P50】如图所示，在 □ ABCD中，AC与BD相交于点 O, EF过点O且与AB和CD都垂直，则OE，OF分别是点O到AB与CD的距离.证明：∵∠OAE=∠OCF，OA=OC,∠AOE=∠COF.∴△OAE≌△OCF.∴OE=OF.【教材P50】证明：∵AE⊥BD 于点E，CF⊥BD于点F，∴AE∥FC.∵四边形ABCD是平行四边形，∴AB∥DC，AB=CD.在Rt△AEB和Rt△CFD中，∵AB = CD，∠ABE=∠CDF，∴ Rt△AEB≌Rt△CFD（AAS） ∴AE=CF.∵AE∥FC，AE=CF , ∴四边形 AECF 为平行四边形.