



还剩11页未读,
继续阅读
初中数学湘教版八年级下册1.1 直角三角形的性质与判定(Ⅰ)课文ppt课件
展开
这是一份初中数学湘教版八年级下册1.1 直角三角形的性质与判定(Ⅰ)课文ppt课件,共19页。PPT课件主要包含了总结归纳,试给出数学证明,图1-1-3等内容,欢迎下载使用。
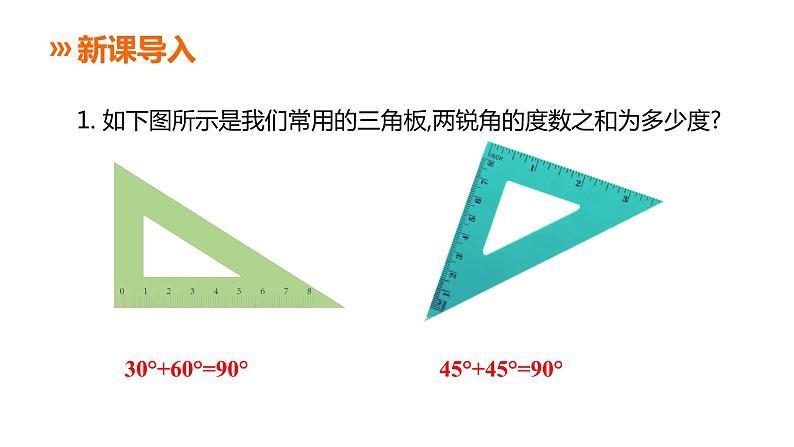
1. 如下图所示是我们常用的三角板,两锐角的度数之和为多少度?
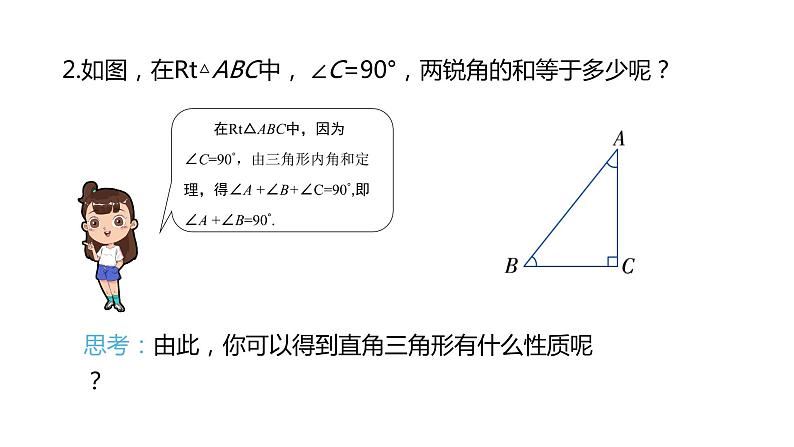
2.如图,在Rt△ABC中, ∠C=90°,两锐角的和等于多少呢?
在Rt△ABC中,因为 ∠C=90°,由三角形内角和定理,得∠A +∠B+∠C=90°,即∠A +∠B=90°.
思考:由此,你可以得到直角三角形有什么性质呢?
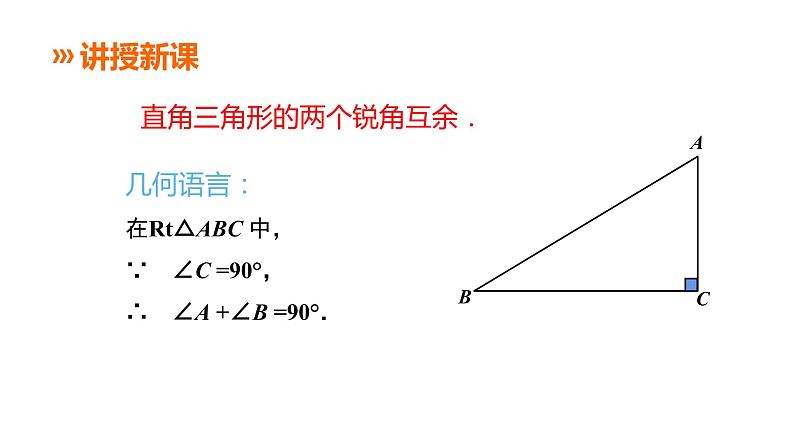
直角三角形的两个锐角互余.
几何语言:在Rt△ABC 中,∵ ∠C =90°,∴ ∠A +∠B =90°.
问题:有两个角互余的三角形是直角三角形吗?
如图,在△ABC中, ∠A +∠B=90° , 那么△ABC是直角三角形吗?
在△ABC中,因为 ∠A +∠B +∠C=180°, 又∠A +∠B=90°,所以∠C=90°. 于是△ABC是直角三角形.
几何语言:在△ABC 中,∵ ∠A +∠B =90°,∴ △ABC 是直角三角形.
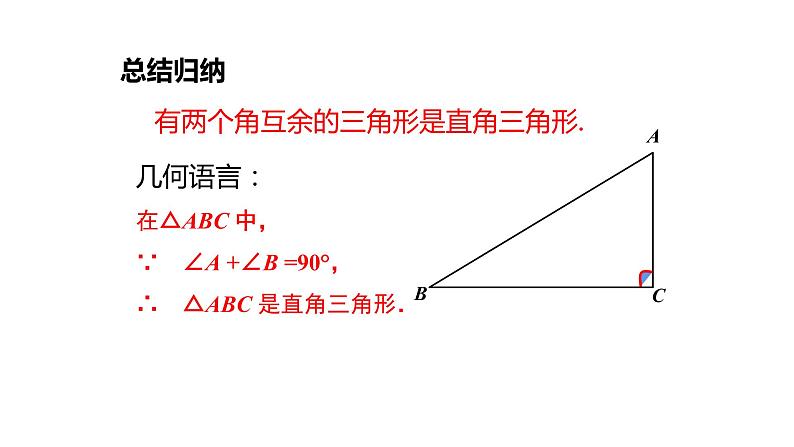
有两个角互余的三角形是直角三角形.
[解析] 可以通过角之间的转化推出∠B+∠C=90°.
证明:∵AD⊥BC,∴∠1+∠C=90°.∵∠1=∠B,∴∠B+∠C=90°,∴△ABC是直角三角形.
【归纳总结】 从角的角度判定直角三角形的两种方法(1)证明三角形的一个角为90°或直角;(2)证明一个三角形中的两个内角的和为90°.
问题: 如图,画一个Rt△ABC, 并作出斜边AB上的中线CD,比较线段CD 与线段AB 之间的数量关系,你能得出什么结论?
线段CD 比线段AB短.
猜想:直角三角形斜边上的中线等于斜边的一半.
【归纳总结】 与直角三角形斜边上的中线有关的结论如图1-1-3,在Rt△ABC中,∠ACB=90°,D为AB的中点,则有下面结论:①AD=BD=CD;②∠A=∠ACD;③∠B=∠BCD;④∠A+∠BCD=90°;⑤∠B+∠ACD=90°.
例4 已知:如图,CD是△ABC的AB边上的中线,且 . 求证:△ABC是直角三角形.
∴ ∠1=∠A,∠2=∠B .
∵∠A+∠B+∠ACB =180°,即∠A+∠B+∠1+∠2=180°, 2(∠A+∠B)=180°.
∴ ∠A+∠B =90°.
∴ △ABC是直角三角形.
1. 如下图所示是我们常用的三角板,两锐角的度数之和为多少度?
2.如图,在Rt△ABC中, ∠C=90°,两锐角的和等于多少呢?
在Rt△ABC中,因为 ∠C=90°,由三角形内角和定理,得∠A +∠B+∠C=90°,即∠A +∠B=90°.
思考:由此,你可以得到直角三角形有什么性质呢?
直角三角形的两个锐角互余.
几何语言:在Rt△ABC 中,∵ ∠C =90°,∴ ∠A +∠B =90°.
问题:有两个角互余的三角形是直角三角形吗?
如图,在△ABC中, ∠A +∠B=90° , 那么△ABC是直角三角形吗?
在△ABC中,因为 ∠A +∠B +∠C=180°, 又∠A +∠B=90°,所以∠C=90°. 于是△ABC是直角三角形.
几何语言:在△ABC 中,∵ ∠A +∠B =90°,∴ △ABC 是直角三角形.
有两个角互余的三角形是直角三角形.
[解析] 可以通过角之间的转化推出∠B+∠C=90°.
证明:∵AD⊥BC,∴∠1+∠C=90°.∵∠1=∠B,∴∠B+∠C=90°,∴△ABC是直角三角形.
【归纳总结】 从角的角度判定直角三角形的两种方法(1)证明三角形的一个角为90°或直角;(2)证明一个三角形中的两个内角的和为90°.
问题: 如图,画一个Rt△ABC, 并作出斜边AB上的中线CD,比较线段CD 与线段AB 之间的数量关系,你能得出什么结论?
线段CD 比线段AB短.
猜想:直角三角形斜边上的中线等于斜边的一半.
【归纳总结】 与直角三角形斜边上的中线有关的结论如图1-1-3,在Rt△ABC中,∠ACB=90°,D为AB的中点,则有下面结论:①AD=BD=CD;②∠A=∠ACD;③∠B=∠BCD;④∠A+∠BCD=90°;⑤∠B+∠ACD=90°.
例4 已知:如图,CD是△ABC的AB边上的中线,且 . 求证:△ABC是直角三角形.
∴ ∠1=∠A,∠2=∠B .
∵∠A+∠B+∠ACB =180°,即∠A+∠B+∠1+∠2=180°, 2(∠A+∠B)=180°.
∴ ∠A+∠B =90°.
∴ △ABC是直角三角形.













