





还剩10页未读,
继续阅读
第10章分式复习课-(苏科版) 课件PPT
展开
这是一份第10章分式复习课-(苏科版) 课件PPT,共18页。
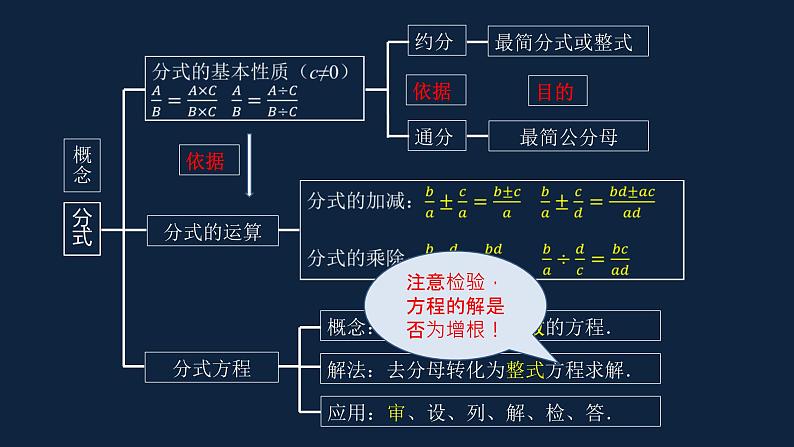
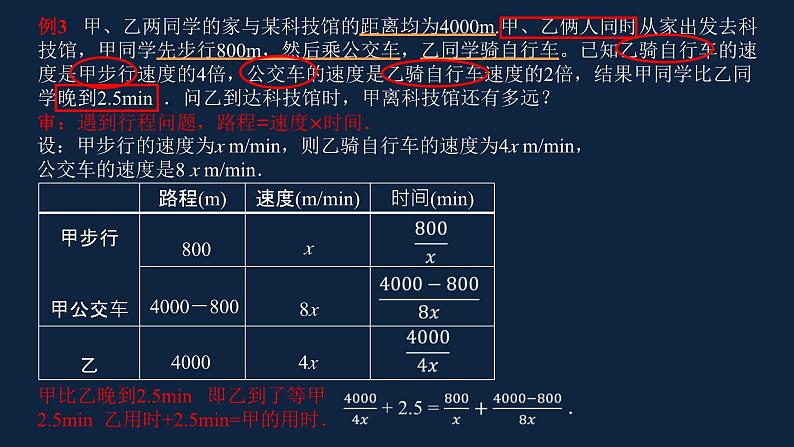
第10章 分式的复习数、式研究的一般路径:温故知新概念性质运算应用(运用).整章从数学和生活的二个视角出发,通过类比和对比小学的分数,用特殊(数)到一般(字母)的研究方法,引入分式概念、性质、运算、应用(运用). 分母B ≠0,分式有意义. 分母B =0,分式无意义. 无 x= 2分式的值为0,要注意:分子为0,且分母≠0 . ∴ x=2.分式 约分最简分式或整式通分最简公分母 目的分式的运算分式方程概念:分母中含有未知数的方程.解法:去分母转化为整式方程求解.应用:审、设、列、解、检、答.注意检验,方程的解是否为增根!依据概念依据 例1 解方程: 去分母(方程两边同时乘以最简公分母)明理 不要漏乘解这个方程,得x=4 . ∴ x=4是原方程的解.可化为一元一次方程的分式方程化为一元一次方程解一元一次方程检验 例1 解方程: 方程两边同乘(x+1)(x-1),得 解这个方程,得x=1 . ∴ x=1是增根,原方程无解.书P118习题2(4)改编 最简公分母为0 分析:如何理解分式方程有增根?分式方程的两边同时乘以式子的值为0 . ∵ 原分式方程有增根, ∴ x=0 或 x=2 .即原分式方程的增根为x=0 或 x=2,把 x=0 和 x=2 分别代入①,得:a=4或a=8 .∴ a=4 或 a=8 . 例3 甲、乙两同学的家与某科技馆的距离均为4000m.甲、乙俩人同时从家出发去科技馆,甲同学先步行800m,然后乘公交车,乙同学骑自行车。已知乙骑自行车的速度是甲步行速度的4倍,公交车的速度是乙骑自行车速度的2倍,结果甲同学比乙同学晚到2.5min .问乙到达科技馆时,甲离科技馆还有多远? 8004000-8004000设:甲步行的速度为x m/min,则乙骑自行车的速度为4x m/min,公交车的速度是8 x m/min.x8x4x 甲比乙晚到2.5min 即乙到了等甲2.5min 乙用时+2.5min=甲的用时. 例3 甲、乙两同学的家与某科技馆的距离均为4000m.甲、乙两人同时从家出发去科技馆,甲同学先步行800m,然后乘公交车,乙同学骑自行车.已知乙骑自行车的速度是甲步行速度的4倍,公交车的速度是乙骑自行车速度的2倍,结果甲同学比乙同学晚到2.5min .问乙到达科技馆时,甲离科技馆还有多远?解:设甲步行的速度为x m/min,则乙骑自行车的速度为4x m/min,公交车的速度是8 x m/min . 解这个方程,得经检验,x=80是所列方程的解,且符合题意.答:乙到达科技馆时,甲离科技馆还有1600m . 审设列解验答根据题意,得x=80 .例3 甲、乙两同学的家与某科技馆的距离均为4000m.甲、乙两人同时从家出发去科技馆,甲同学先步行800m,然后乘公交车,乙同学骑自行车.已知乙骑自行车的速度是甲步行速度的4倍,公交车的速度是乙骑自行车速度的2倍,结果甲同学比乙同学晚到2.5min .问乙到达科技馆时,甲离科技馆还有多远?解:设甲步行的速度为x m/min,则乙骑自行车的速度为4x m/min,公交车的速度是8 x m/min. 变式:这里是2个人同时出发,甲同学比乙同学晚到2.5min ,小结:学会列表,把文字信息集中在表格,通过时间建立等量关系.早到课后思考:自主编题(只列方程不求解) 比如本题中,甲先出发2.5min,结果比乙早到2分钟?同时到达?晚到2分钟?根据题意,得 拓展提升 A.a>-1 B.a>-1且a≠0 C.a<-1 D.a<-1且a≠-2 分析:关于x的方程,即x为方程的主元,即未知数为x.方程的解为正数,即x>0 .由于本题是分式方程,x≠1 .∴ x>0且x≠1 .原方程去分母后,得 2x+a=x-1 .∴ x=-1-a . ∵ x>0且x≠1 . 注意分母≠0的隐蔽条件.D 思维提升 一元二次方程不会解?试出错误!回头再思考.从式的结构角度去思考!对已知进行两边平方,可能会与结论产生关联. 积累解题经验,培养解题感觉. 变式: 从熟悉入手,从式的形式寻关联. 经验转化: 继续升华 分析:从已知ab=1入手,感觉没有头绪,则尝试把结论通分. 法2: 抓住填空题的特征.∵ ab=1,∴令a=1,b=1,代入原式=1.《课课练》P87第13题赋值法,特殊代替一般小结 本课重点研究了分式方程和分式方程的应用(运用),解分式方程时要注意不要漏乘,要进行检验,注意增根!应用题要重分析,学会用图表等方法去分析,注意整体思想的运用,要注意观察数(式)的结构,大胆尝试和探究,积累解题经验,培养解题感觉. 分式和分数一样都能描述现实世界中的数量关系,分式方程与其他方程一样,是刻画现实世界数量关系的有效模型。学会用类比的思想思考问题,用对比的眼光观察问题,用转化的方法解决问题.作业 6.我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货,每月实际生产智能手机多少万部?7.某校组织学生去9km外的郊区游玩,一部分学生骑自行车先走,半小时后,其他学生乘公共汽车出发,结果他们同时到达.已知公共汽车的速度是自行车速度的3倍,自行车的速度和公共汽车的速度分别是多少?
第10章 分式的复习数、式研究的一般路径:温故知新概念性质运算应用(运用).整章从数学和生活的二个视角出发,通过类比和对比小学的分数,用特殊(数)到一般(字母)的研究方法,引入分式概念、性质、运算、应用(运用). 分母B ≠0,分式有意义. 分母B =0,分式无意义. 无 x= 2分式的值为0,要注意:分子为0,且分母≠0 . ∴ x=2.分式 约分最简分式或整式通分最简公分母 目的分式的运算分式方程概念:分母中含有未知数的方程.解法:去分母转化为整式方程求解.应用:审、设、列、解、检、答.注意检验,方程的解是否为增根!依据概念依据 例1 解方程: 去分母(方程两边同时乘以最简公分母)明理 不要漏乘解这个方程,得x=4 . ∴ x=4是原方程的解.可化为一元一次方程的分式方程化为一元一次方程解一元一次方程检验 例1 解方程: 方程两边同乘(x+1)(x-1),得 解这个方程,得x=1 . ∴ x=1是增根,原方程无解.书P118习题2(4)改编 最简公分母为0 分析:如何理解分式方程有增根?分式方程的两边同时乘以式子的值为0 . ∵ 原分式方程有增根, ∴ x=0 或 x=2 .即原分式方程的增根为x=0 或 x=2,把 x=0 和 x=2 分别代入①,得:a=4或a=8 .∴ a=4 或 a=8 . 例3 甲、乙两同学的家与某科技馆的距离均为4000m.甲、乙俩人同时从家出发去科技馆,甲同学先步行800m,然后乘公交车,乙同学骑自行车。已知乙骑自行车的速度是甲步行速度的4倍,公交车的速度是乙骑自行车速度的2倍,结果甲同学比乙同学晚到2.5min .问乙到达科技馆时,甲离科技馆还有多远? 8004000-8004000设:甲步行的速度为x m/min,则乙骑自行车的速度为4x m/min,公交车的速度是8 x m/min.x8x4x 甲比乙晚到2.5min 即乙到了等甲2.5min 乙用时+2.5min=甲的用时. 例3 甲、乙两同学的家与某科技馆的距离均为4000m.甲、乙两人同时从家出发去科技馆,甲同学先步行800m,然后乘公交车,乙同学骑自行车.已知乙骑自行车的速度是甲步行速度的4倍,公交车的速度是乙骑自行车速度的2倍,结果甲同学比乙同学晚到2.5min .问乙到达科技馆时,甲离科技馆还有多远?解:设甲步行的速度为x m/min,则乙骑自行车的速度为4x m/min,公交车的速度是8 x m/min . 解这个方程,得经检验,x=80是所列方程的解,且符合题意.答:乙到达科技馆时,甲离科技馆还有1600m . 审设列解验答根据题意,得x=80 .例3 甲、乙两同学的家与某科技馆的距离均为4000m.甲、乙两人同时从家出发去科技馆,甲同学先步行800m,然后乘公交车,乙同学骑自行车.已知乙骑自行车的速度是甲步行速度的4倍,公交车的速度是乙骑自行车速度的2倍,结果甲同学比乙同学晚到2.5min .问乙到达科技馆时,甲离科技馆还有多远?解:设甲步行的速度为x m/min,则乙骑自行车的速度为4x m/min,公交车的速度是8 x m/min. 变式:这里是2个人同时出发,甲同学比乙同学晚到2.5min ,小结:学会列表,把文字信息集中在表格,通过时间建立等量关系.早到课后思考:自主编题(只列方程不求解) 比如本题中,甲先出发2.5min,结果比乙早到2分钟?同时到达?晚到2分钟?根据题意,得 拓展提升 A.a>-1 B.a>-1且a≠0 C.a<-1 D.a<-1且a≠-2 分析:关于x的方程,即x为方程的主元,即未知数为x.方程的解为正数,即x>0 .由于本题是分式方程,x≠1 .∴ x>0且x≠1 .原方程去分母后,得 2x+a=x-1 .∴ x=-1-a . ∵ x>0且x≠1 . 注意分母≠0的隐蔽条件.D 思维提升 一元二次方程不会解?试出错误!回头再思考.从式的结构角度去思考!对已知进行两边平方,可能会与结论产生关联. 积累解题经验,培养解题感觉. 变式: 从熟悉入手,从式的形式寻关联. 经验转化: 继续升华 分析:从已知ab=1入手,感觉没有头绪,则尝试把结论通分. 法2: 抓住填空题的特征.∵ ab=1,∴令a=1,b=1,代入原式=1.《课课练》P87第13题赋值法,特殊代替一般小结 本课重点研究了分式方程和分式方程的应用(运用),解分式方程时要注意不要漏乘,要进行检验,注意增根!应用题要重分析,学会用图表等方法去分析,注意整体思想的运用,要注意观察数(式)的结构,大胆尝试和探究,积累解题经验,培养解题感觉. 分式和分数一样都能描述现实世界中的数量关系,分式方程与其他方程一样,是刻画现实世界数量关系的有效模型。学会用类比的思想思考问题,用对比的眼光观察问题,用转化的方法解决问题.作业 6.我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货,每月实际生产智能手机多少万部?7.某校组织学生去9km外的郊区游玩,一部分学生骑自行车先走,半小时后,其他学生乘公共汽车出发,结果他们同时到达.已知公共汽车的速度是自行车速度的3倍,自行车的速度和公共汽车的速度分别是多少?
相关资料
更多









