

还剩8页未读,
继续阅读
第十一章反比例函数小结-(苏科)课件PPT
展开
这是一份第十一章反比例函数小结-(苏科)课件PPT,共15页。
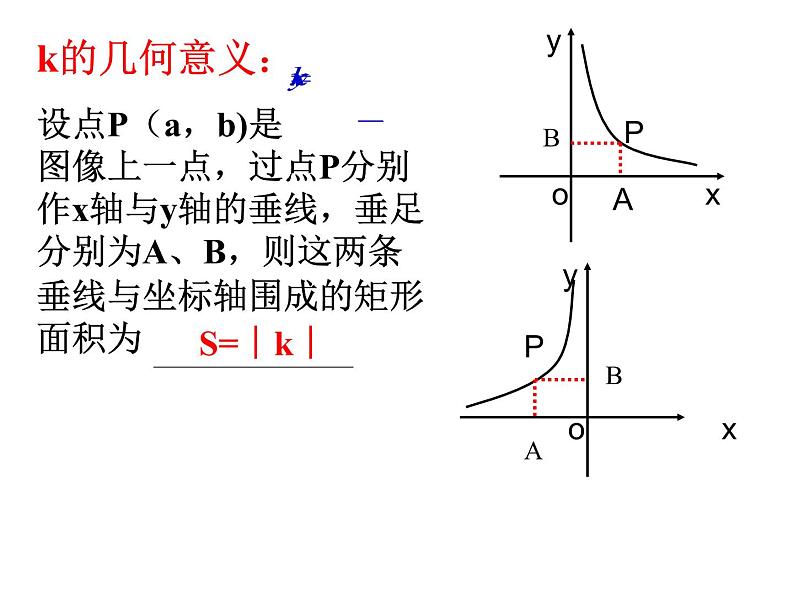
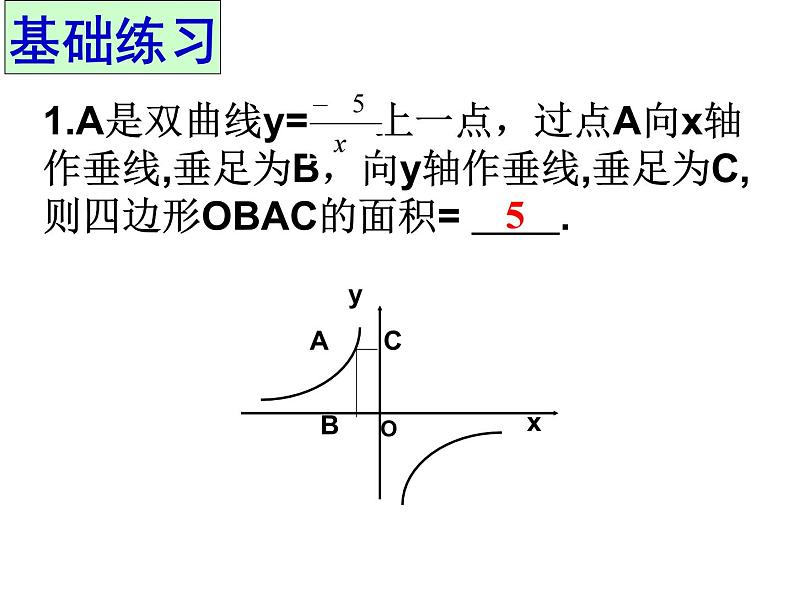
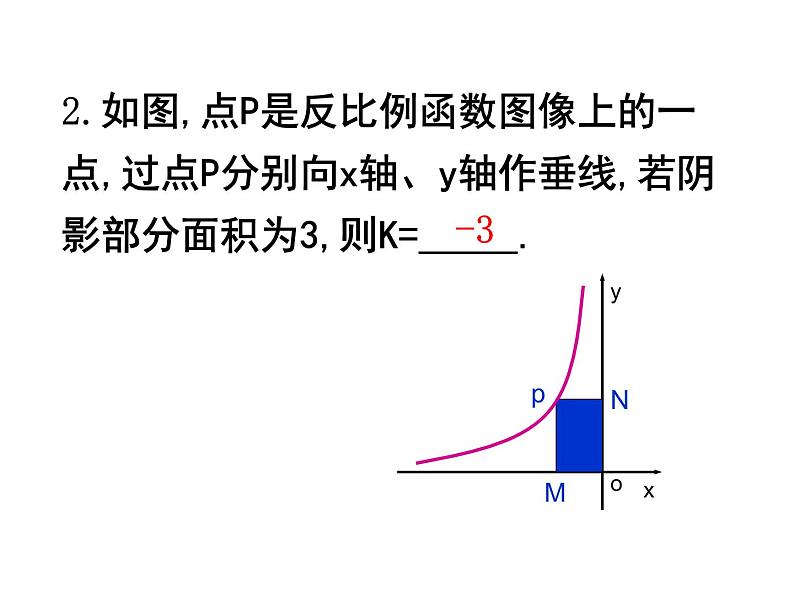
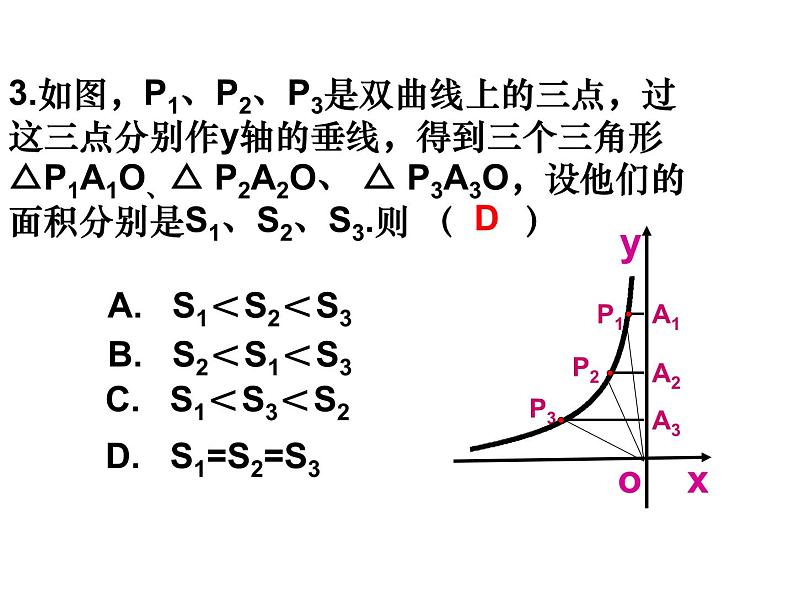
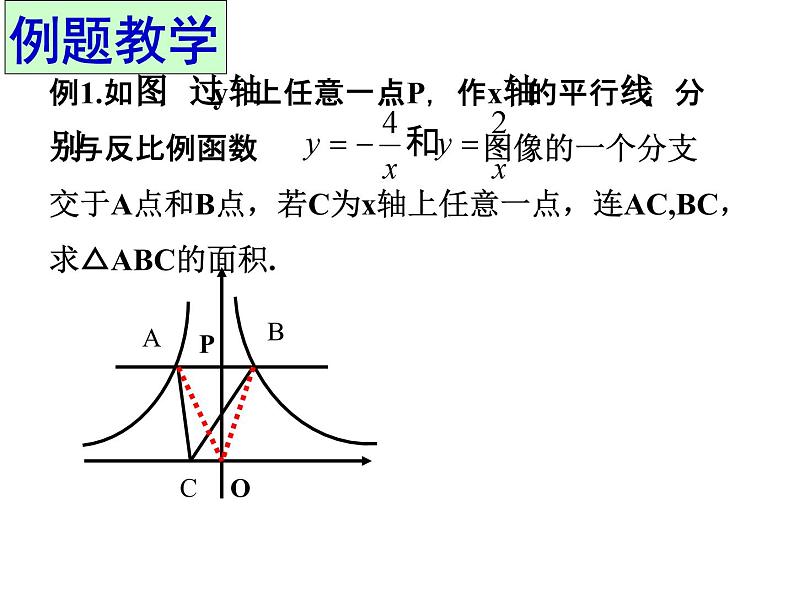
复习反比例函数yBk的几何意义:设点P(a,b)是 图像上一点,过点P分别作x轴与y轴的垂线,垂足分别为A、B,则这两条垂线与坐标轴围成的矩形面积为S=︱k︱1.A是双曲线y= 上一点,过点A向x轴作垂线,垂足为B,向y轴作垂线,垂足为C,则四边形OBAC的面积= .O52.如图,点P是反比例函数图像上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则K= .-33.如图,P1、P2、P3是双曲线上的三点,过这三点分别作y轴的垂线,得到三个三角形△P1A1O、△ P2A2O、 △ P3A3O,设他们的面积分别是S1、S2、S3.则 ( )A. S1<S2<S3B. S2<S1<S3C. S1<S3<S2D. S1=S2=S3D 已知反比例函数 与点A (1,5),从面积的角度(可适当添加点A1(-1,-5)或(5,1)或双曲线 )编写数学题。思维畅想例1.如图,过y轴上任意一点P,作x轴的平行线,分别与反比例函数 图像的一个分支交于A点和B点,若C为x轴上任意一点,连AC,BC,求△ABC的面积.OP1.如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数 y= (x>0)和y= (x>0)的图像交于P、Q、两点,若S△POQ=14,则k的值为_______.-202.如图,点A是反比例函数y1 = (x>0)图像上一点,过点A作x轴的平行线,交反比例函数 y2= (x>0)的图像于点B,连接OA、OB,若△OAB的面积为2,则k的值为________. C53.如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD反向延长线交y轴负半轴于E,反比例函数y= (x>0)的图像经过点A,S△BEC=10,则k等于______.20例(1)S△OAF=S△OCE (2)S△OFB=S△OEB(3)当点F是AB的中点 时,则点E是BC的中点 (4)当BF=nAF时BE=nCE1.如图,在平面直角坐标系中,反比例函数 y= (x>0)的图像交矩形OABC的边AB于点D,交边BC 于E,BE=2EC.若四边形ODBE的面积为6,则k=____.32.如图,反比例函数y= 和y= 在第一象限内的图像如图所示,点M在y= 的图像上,MC⊥x轴于点C,MD⊥y轴于点D,交y= 的图像分别于A、B两点,则 △OAB的面积=______.3.如图,矩形OMPN的顶点M、N分别在x轴和y轴的正半轴上,点C为对角线OP的中点,反比例函数 y= 在第一象限内的图像经过点C,且与MP 、NP分别交于A、B两点,若四边形ACBP的面积为4.5,求k的值. C课堂感悟谈谈你的收获与体会
复习反比例函数yBk的几何意义:设点P(a,b)是 图像上一点,过点P分别作x轴与y轴的垂线,垂足分别为A、B,则这两条垂线与坐标轴围成的矩形面积为S=︱k︱1.A是双曲线y= 上一点,过点A向x轴作垂线,垂足为B,向y轴作垂线,垂足为C,则四边形OBAC的面积= .O52.如图,点P是反比例函数图像上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则K= .-33.如图,P1、P2、P3是双曲线上的三点,过这三点分别作y轴的垂线,得到三个三角形△P1A1O、△ P2A2O、 △ P3A3O,设他们的面积分别是S1、S2、S3.则 ( )A. S1<S2<S3B. S2<S1<S3C. S1<S3<S2D. S1=S2=S3D 已知反比例函数 与点A (1,5),从面积的角度(可适当添加点A1(-1,-5)或(5,1)或双曲线 )编写数学题。思维畅想例1.如图,过y轴上任意一点P,作x轴的平行线,分别与反比例函数 图像的一个分支交于A点和B点,若C为x轴上任意一点,连AC,BC,求△ABC的面积.OP1.如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数 y= (x>0)和y= (x>0)的图像交于P、Q、两点,若S△POQ=14,则k的值为_______.-202.如图,点A是反比例函数y1 = (x>0)图像上一点,过点A作x轴的平行线,交反比例函数 y2= (x>0)的图像于点B,连接OA、OB,若△OAB的面积为2,则k的值为________. C53.如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD反向延长线交y轴负半轴于E,反比例函数y= (x>0)的图像经过点A,S△BEC=10,则k等于______.20例(1)S△OAF=S△OCE (2)S△OFB=S△OEB(3)当点F是AB的中点 时,则点E是BC的中点 (4)当BF=nAF时BE=nCE1.如图,在平面直角坐标系中,反比例函数 y= (x>0)的图像交矩形OABC的边AB于点D,交边BC 于E,BE=2EC.若四边形ODBE的面积为6,则k=____.32.如图,反比例函数y= 和y= 在第一象限内的图像如图所示,点M在y= 的图像上,MC⊥x轴于点C,MD⊥y轴于点D,交y= 的图像分别于A、B两点,则 △OAB的面积=______.3.如图,矩形OMPN的顶点M、N分别在x轴和y轴的正半轴上,点C为对角线OP的中点,反比例函数 y= 在第一象限内的图像经过点C,且与MP 、NP分别交于A、B两点,若四边形ACBP的面积为4.5,求k的值. C课堂感悟谈谈你的收获与体会
相关资料
更多









