




数学九年级上册22.1.1 二次函数集体备课ppt课件
展开二次函数与一元二次方程的关系
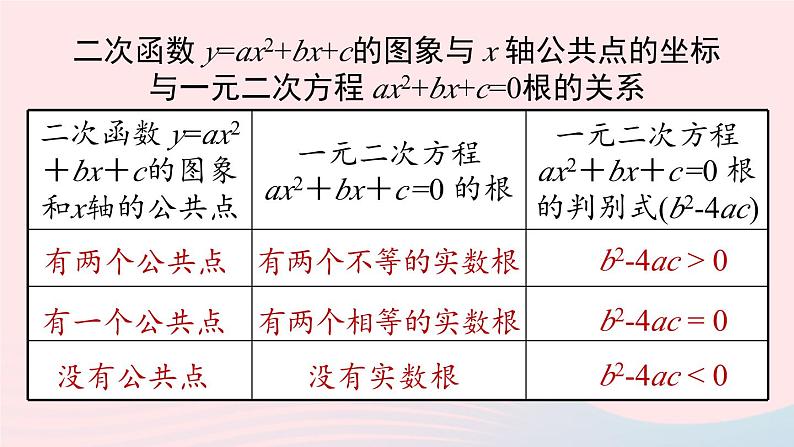
二次函数 y=ax2+bx+c 的图象和 x 轴的公共点有三种情况:有两个公共点,有一个公共点,没有公共点.当二次函数 y=ax2+bx+c 的图象和 x 轴有公共点时,公共点的横坐标就是当 y=0时自变量 x 的值,即一元二次方程 ax2+bx+c=0 的根.
抛物线 y=ax2+bx+c(a≠0)与x轴的公共点的横坐标即一元二次方程ax2+bx+c =0的根
二次函数与一元二次方程
抛物线与 x 轴的公共点情况
利用图象法求一元二次方程的根
抛物线与直线的公共点个数
二次函数 y=ax2+bx+c的图象与 x 轴公共点的坐标与一元二次方程 ax2+bx+c=0根的关系
有两个公共点x1,x2 (x1<x2)
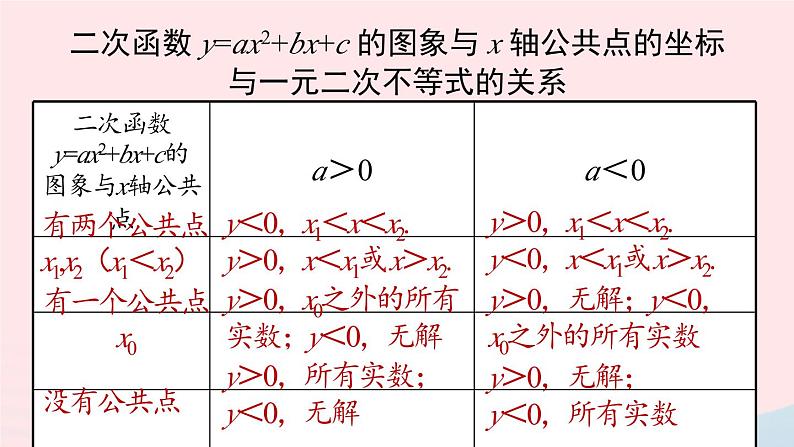
二次函数 y=ax2+bx+c 的图象与 x 轴公共点的坐标与一元二次不等式的关系
y<0,x1<x<x2.y>0,x<x1或 x>x2.
y>0,x1<x<x2.y<0,x<x1或 x>x2.
y>0,x0之外的所有实数;y<0,无解
y>0,无解;y<0,x0之外的所有实数
y>0,所有实数;y<0,无解
y>0,无解;y<0,所有实数
二次函数y=ax2+bx+c
利用二次函数的图象和性质求解
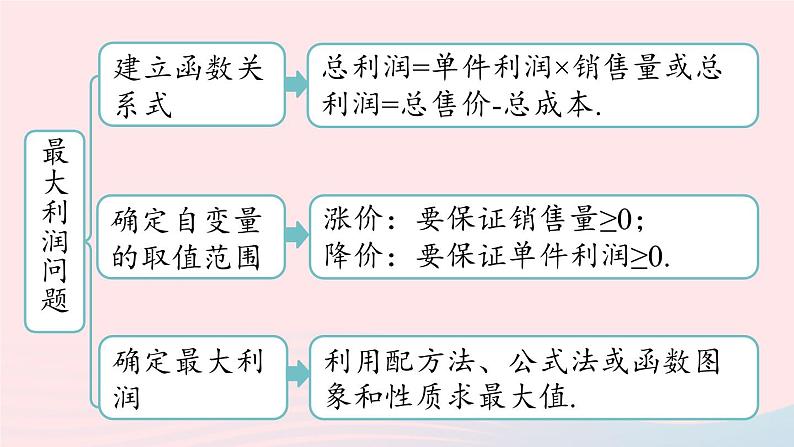
利用二次函数解决实际问题
用二次函数解决实际问题的一般步骤:
1.审:仔细审题,厘清题意.2.设:找出题中的变量和常量,分析它们之间的关系,设出适当的未知数.3.列:用二次函数表示出变量和常量之间的关系,建立二次函数模型,写出二次函数的解析式.4.解:依据已知条件,借助二次函数的解析式、图象和性质等求解实际问题.5.检:检验结果,进行合理取舍.
总利润=单件利润×销售量或总利润=总售价-总成本.
涨价:要保证销售量≥0;降价:要保证单件利润≥0.
利用配方法、公式法或函数图象和性质求最大值.
(二次函数的图象和性质)
(实物中的抛物线形问题)
能够将实际距离准确的转化为点的坐标;选择简便的运算方法.
1.若二次函数 y=x2+mx 的对称轴是 x=3,则关于 x 的方程 x2+mx=7 的解为( )A. x1=0,x2=6B. x1=1,x2=7C. x1=1,x2=﹣7D. x1=﹣1,x2=7
2.某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量 y(件)与销售单价 x(元)符合一次函数 y=kx+b,且 x=65时,y=55;x=75时,y=45.(1)求一次函数的解析式;
解得k=-1,b=120.故所求一次函数的解析式为 y=-x+120.
解:(2) W=(x-60)(-x+120)= -x2+180x-7 200= -(x-90)2+900,
∵抛物线的开口向下, ∴当x<90时,W 随x的增大而增大,而60≤x≤60(1+45%),即60≤x≤87,∴当x=87时,W有最大值,此时W=-(87-90)2+900=891.
2.某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量 y(件)与销售单价 x(元)符合一次函数 y=kx+b,且 x=65时,y=55;x=75时,y=45.(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
3.如图,在梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°,AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.(1) 用含有x的代数式表示BF的长;
解:(1) 由题意, 得EF=AE=DE=BC=x ,AB=30. ∴BF=2x-30.
3.如图,在梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°,AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G. (2) 设四边形DEBG的面积为S,求S与x的函数关系式;
3.如图,在梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°,AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G. (3) 当x为何值时,S有最大值?并求出这个最大值.
4.一位运动员在距篮下4 m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5 m时,达到最大高度3.5 m,然后准确落入篮圈.如图所示,建立平面直角坐标系,已知篮圈中心到地面的距离为3.05 m,该运动员身高1.9 m,在这次跳投中,球与头顶上方的距离为0.25 m,则运动员跳离地面的高度是( )
0.1 m0.2 mC. 0.3 mD. 0.4 m
解:设抛物线的解析式为 y=ax2+3.5.由图知图象过点(1.5,3.05).∴2.25a+3.5=3.05,解得a=-0.2,∴抛物线的解析式为 y=-0.2x2+3.5.设球出手时,运动员跳离地面的高度为h m.∵y=-0.2x2+3.5,∴h+1.9+0.25=-0.2×(-2.5)2+3.5,∴h=0.1 .故选A.
1.已知二次函数 y=(x-p)(x-q)+2,若 m,n是关于 x 方程(x-p)(x-q)+2=0的两个根,则实数m,n,p,q的大小关系可能是( )
A. m<p<q<nB. m<p<n<qC. p<m<n<qD. p<m<q<n
y=(x-p)(x-q)+2
2.张大伯准备用40 m长的木栏围一个矩形的羊圈,为了节约材料同时要使矩形的面积最大,他利用了自家房屋一面长25 m的墙,设计了如图一个矩形的羊圈.(1) 请你求出矩形羊圈的面积;
解:(1)由题意,得羊圈的长为25 m, 宽为(40-25)÷2=7.5(m). 故羊圈的面积为25×7.5=187.5(m2)
解:(2) 设羊圈与墙垂直的一边长为x m,则与墙平行的一边长为(40-2x) m,羊圈的面积S=x(40-2x)=-2x2+40x =-2(x-10)2+200(0<x<20).∴当x=10时,S有最大值,此时S=200.∵200>187.5,∴张大伯的设计不合理.应当设计羊圈与墙垂直的两边长为10 m,与墙平行的一边长为20m.
(2) 请你判断他的设计方案是否合理?如果合理,直接答合理;如果不合理又该如何设计?并说明理由.
3.一家电脑公司推出一款新型电脑,投放市场以来3个月的利润情况如图所示,该图可以近似看为抛物线的一部分,请结合图象,解答以下问题:
(1)求该抛物线对应的二次函数解析式.
故所求二次函数的解析式为y=-x2+14x.
(2) 该公司在经营此款电脑过程中,第几月的利润最大?最大利润是多少?
解:(2) y=-x2+14x=-(x-7)2+49.当x=7时,y最大值=49,即第7个月的利润最大,为49万元.
解:(3) 没有利润,即y=-x2+14x=0,解得x1=0(舍去),x2=14.所以第15个月,改公司开始亏损.
(3) 若照此经营下去,请你结合所学的知识,对此款电脑的经营状况(是否亏损?何时亏损)做预测分析.
解(2)∵GM= 2 m,∴OM=OG=1 m.
答:每个B型活动板房的成本是500元.
4.(2020•青岛中考)某公司生产A型活动板房成本是每个425元.图①表示A型活动板房的一面墙,它由长方形和抛物线构成,长方形的长AD=4 m,宽AB=3 m,抛物线的最高点E到BC的距离为4 m.(3)根据市场调查,以单价650元销售(2)中的B型活动板房,每月能售出100个,而单价每降低10元,每月能多售出20个.公司每月最多能生产160个B型活动板房.不考虑其他因素,公司将销售单价n(元)定为多少时,每月销售B型活动板房所获利润w(元)最大?最大利润是多少?
初中数学人教版九年级上册22.1.1 二次函数教课课件ppt: 这是一份初中数学人教版九年级上册22.1.1 二次函数教课课件ppt,共19页。PPT课件主要包含了二次函数的概念,知识梳理,二次函数的解析式,二次函数图象及性质,函数解析式,图象特征,函数性质,增减性,对称轴,抛物线的平移规律等内容,欢迎下载使用。
初中数学人教版九年级上册22.3 实际问题与二次函数多媒体教学ppt课件: 这是一份初中数学人教版九年级上册22.3 实际问题与二次函数多媒体教学ppt课件,共23页。PPT课件主要包含了知识回顾,学习目标,课堂导入,知识点1,新知探究,本题源于《教材帮》,跟踪训练,知识点2,随堂练习,拱桥问题等内容,欢迎下载使用。
人教版九年级上册22.3 实际问题与二次函数评课ppt课件: 这是一份人教版九年级上册22.3 实际问题与二次函数评课ppt课件,共24页。PPT课件主要包含了知识回顾,学习目标,课堂导入,解法一配方法,解法二公式法,新知探究,知识点,跟踪训练,随堂练习,几何面积最值问题等内容,欢迎下载使用。













