高中数学人教A版 (2019)选择性必修 第三册第六章 计数原理6.1 分类加法计数原理与分步乘法计数原理第1课时同步测试题

6.1 分类加法计数原理与分步乘法计数原理 第1课时 两个计数原理及其简单应用

A级　基础巩固

1.某同学从4本不同的科普杂志、3本不同的文摘杂志、2本不同的娱乐新闻杂志中任选1本阅读,则不同的选法共有(　　)

A.24种B.9种 C.3种D.26种

解析:由分类加法计数原理可知,共有4+3+2=9种不同的选法,

故选B.

答案:B

2.若a∈{3,4,6},b∈{1,2},r∈{1,4,9,16},则方程(x-a)2+(y-b)2=r2可表示的不同圆的个数是(　　)

A.6B.9C.16D.24

解析:确定一个圆的方程可分为三个步骤:

第一步,确定a,有3种选法;

第二步,确定b,有2种选法;

第三步,确定r,有4种选法.

由分步乘法计数原理,得不同圆的个数为3×2×4=24.

答案:D

3.已知集合M={1,-2,3},N={-4,5,6,-7},若从两个集合中各取一个元素作为点的坐标,则这样的坐标在平面直角坐标系中可表示第一、第二象限内不同的点的个数是(　　)

A.18B.17C.16　D.14

解析:分两类:第一类,M中的元素作横坐标,N中的元素作纵坐标,则在第一、第二象限内不同的点的个数为3×2=6;

第二类,N中的元素作横坐标,M中的元素作纵坐标,则在第一、第二象限内不同的点的个数为4×2=8.

由分类加法计数原理可知,

共有6+8=14个不同的点在第一、第二象限.

答案:D

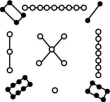
4.洛书,古称龟书,是阴阳五行术数之源.相传大禹治水之时,有神龟出于洛水,其背上长有纹、图、点,自列成组,这就是“洛书”.结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,五方白圈皆阳数,四角黑点为阴数,如图.若从四个阴数和五个阳数中各随机选取1个数,则选取的两数之和能被5整除的概率为(　　)

A.B.C.D.

解析:由题意可知,阴数为2,4,6,8,阳数为1,3,5,7,9.各选一个数,共有4×5=20种选法.两数之和能被5整除的有(2,3),(4,1),(6,9),(8,7)共4个,根据古典概率公式可得P==.

答案:C

5.某元宵灯谜竞猜节目,有6名守擂选手和6名复活选手,若从复活选手中挑选1名选手为攻擂者,从守擂选手中挑选1名选手为守擂者,则攻擂者、守擂者的不同构成方式共有36种.

解析:从6名守擂选手中任选1名,选法有6种;

从6名复活选手中任选1名,选法有6种.

由分步乘法计数原理,得不同的构成方式的种数为6×6=36.

6.有一项活动,需在3名老师、8名男同学和5名女同学中选人参加.

(1)若只需1人参加,有多少种不同选法?

(2)若需老师、男同学、女同学各1人参加,有多少种不同选法?

(3)若需1名老师、1名学生参加,有多少种不同选法?

解:(1)根据分类加法计数原理可得,只需1人参加,有3+8+5=16种不同选法.

(2)根据分步乘法计数原理可得,需老师、男同学、女同学各1人参加,有3×8×5=120种不同选法.

(3)根据分类加法计数原理和分步乘法计数原理可得,需1名老师、1名学生参加,有3×(8+5)=39种不同选法.

B级　拓展提高

7.晓芳有4件不同颜色的衬衣、3件不同样式的裤子,另有2套不同样式的连衣裙.“五一”需选择1套服装参加歌舞演出,则晓芳不同的穿衣服的方式有(　　)

A.24种B.14种 C.10种 D.9种

解析:首先分两类:第一类是穿衬衣和裤子,由分步乘法计数原理,知共有4×3=12种穿衣服的方式;第二类是穿连衣裙,有2种穿衣方式.所以由分类加法计数原理,知共有12+2=14种穿衣服的方式.

答案:B

8.现有6名同学去听同时进行的5个课外知识讲座,每名同学可自由选择其中的任意一个讲座,不同选法的种数是(　　)

A.56

B.65

C.

D.6×5×4×3×2

解析:每名同学都有5种选择,故共有5×5×5×5×5×5=56种选法.

答案:A

9.数学与文学有许多奇妙的联系,如诗中的回文诗“儿忆父兮妻忆夫”,既可以顺读也可以逆读.数学中的回文数,如343,12 521等.两位数的回文数有11,22,33,…,99共9个,则在三位数的回文数中偶数的个数是40.

解析:由题意,若三位数的回文数是偶数,则末(首)位可能为2,4,6,

8.如果末(首)位为2,中间一位数有10种可能,同理可得,如果末(首)位为4或6或8,中间一位数均有10种可能,所以有4×10=40个.

10.现有高一年级四个班的学生34人,其中(1)(2)(3)(4)班分别有7人、8人、9人、10人,他们自愿组成数学课外小组.

(1)选其中1人为负责人,有多少种不同的选法?

(2)每班选1人任组长,有多少种不同的选法?

(3)推选2人发言,这2人需来自不同的班级,有多少种不同的选法?

解:(1)分四类:

第一类,从(1)班学生中任选1人,有7种选法;

第二类,从(2)班学生中任选1人,有8种选法;

第三类,从(3)班学生中任选1人,有9种选法;

第四类,从(4)班学生中任选1人,有10种选法.

所以不同的选法种数为7+8+9+10=34.

(2)分四步:

第一步、第二步、第三步、第四步分别从(1)(2)(3)(4)班学生中选1人任组长,所以不同的选法种数为7×8×9×10=5 040.

(3)分六类,每类又分两步:

从(1)(2)班学生中各选1人,有7×8种不同的选法;

从(1)(3)班学生中各选1人,有7×9 种不同的选法;

从(1)(4)班学生中各选1人,有7×10种不同的选法;

从(2)(3)班学生中各选1人,有8×9种不同的选法;

从(2)(4)班学生中各选1人,有8×10种不同的选法;

从(3)(4)班学生中各选1人,有9×10种不同的选法.

所以不同的选法种数为7×8+7×9+7×10+8×9+8×10+9×10=431.

C级　挑战创新

11.多空题从2,3,5,7,11这5个数中每次选出2个不同的数作为分数的分子、分母,则可产生不同的分数的个数是20,其中真分数的个数是10.

解析:产生分数可分两步:第一步,产生分子有5种方法;第二步,产生分母有4种方法,共有5×4=20个分数.产生真分数,可分四类:第一类,当分子是2时,有4个真分数;同理,当分子分别是3,5,7时,真分数的个数分别是3,2,1,共有4+3+2+1=10个真分数.

12.多空题从-1,0,1,2这4个数中选3个不同的数作为函数f(x)=ax2+

bx+c的各项系数,可组成不同的二次函数共18个,其中不同的偶函数有6个.(用数字作答)

解析:一个二次函数对应着a,b,c(a≠0)的一组取值,a的取法有3种,b的取法有3种,c的取法有2种,由分步乘法计数原理,知组成不同的二次函数的个数为3×3×2=18.其中不同的偶函数(b=0)的个数为1×3×2=6.

13.多空题如图①,在电路中合上一个开关以接通电路,有5种不同的方法;如图②,在电路中合上两个开关以接通电路,有6种不同的方法.

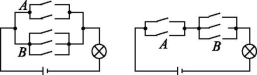
　　　　　图①图②

解析:对于题图①,按要求接通电路,只需将A部分中的两个开关或B部分中的三个开关合上一个即可,故有2+3=5种不同的方法.

对于题图②,按要求接通电路必须分两步进行:

第1步,合上A部分中的一个开关,第2步,合上B部分中的一个开关,故有2×3=6种不同的方法.