



还剩15页未读,
继续阅读
成套系列资料,整套一键下载
5.1.1函数的概念(1)课件-2023-2024学年高一上学期数学苏教版(2019)必修第一册
展开
这是一份5.1.1函数的概念(1)课件-2023-2024学年高一上学期数学苏教版(2019)必修第一册,共23页。
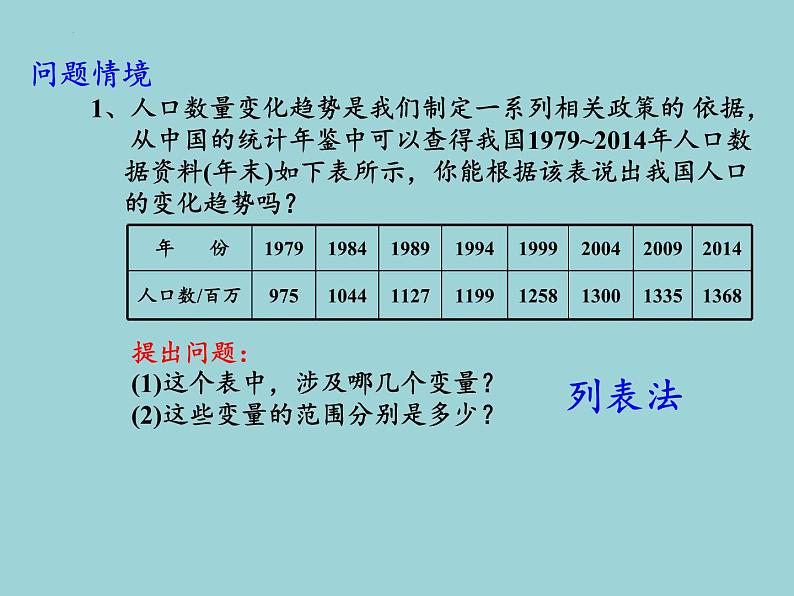
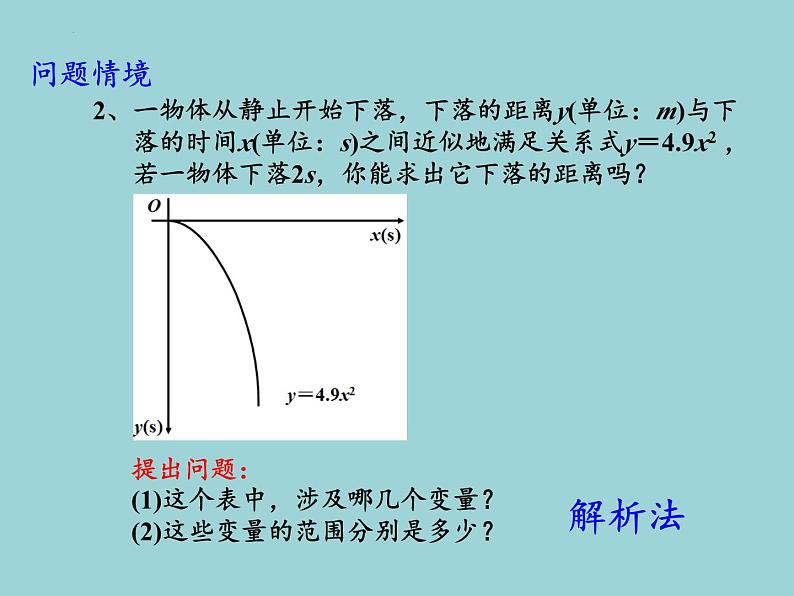
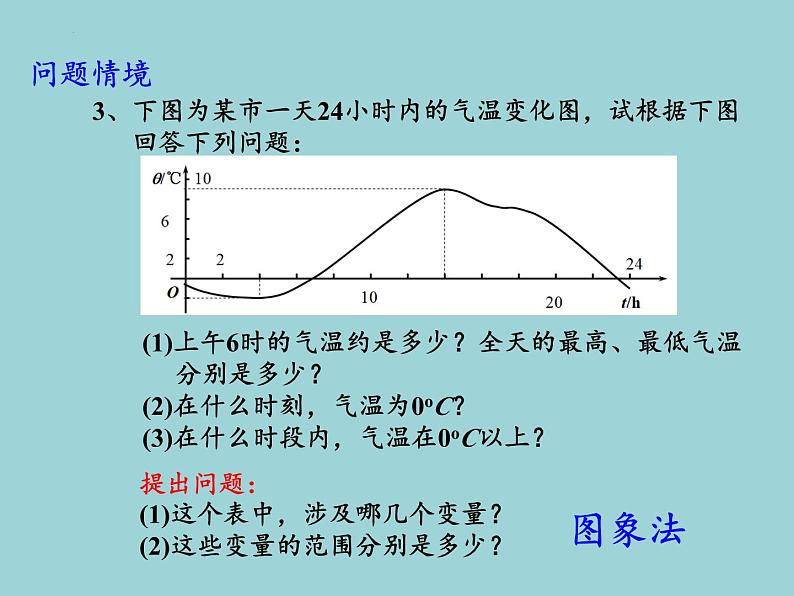
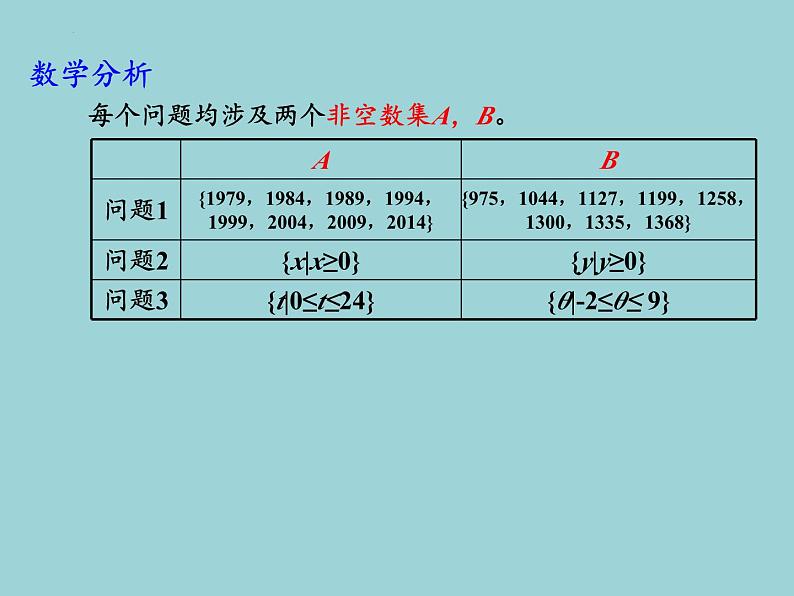
函数的概念(1)课前导入我们的生活的世界时刻都在发生变化,变化无处不在。这些变化着的现象都可以用数学来有效地描述。函数是描述客观世界变化规律的重要数学模型,函数模型可以帮助我们解决许多实际问题。因此,学习函数知识对研究客观世界、掌握事物变化规律具有重要的意义。函数是本章的核心概念,也是中学数学中的基本概念。高中阶段不仅把函数看成变量之间的依赖关系,同时还用集合与对应的语言刻画函数,函数的思想将贯穿整个高中数学课程。复习回顾1、初中学过的函数的概念如何表述一般地,如果在一个变化过程中,有两个 变量 x和y,对于x的每一个值, y都有唯一的 值与之对应,我们就说y是x的函数,x是自变量。2、常用的表示函数关系的方法(1)解析法;(2)列表法;(3)图象法。复习回顾3、初中所学常见的函数模型(3)一次函数的一般形式为:y = kx+b(k≠0);(4)二次函数的一般形式:y = ax2+bx+c (a、b、c 是常数 ,a≠0)。(1)正比例函数的一般形式为:y = kx (k≠0);问题情境1、人口数量变化趋势是我们制定一系列相关政策的 依据, 从中国的统计年鉴中可以查得我国1979~2014年人口数 据资料(年末)如下表所示,你能根据该表说出我国人口 的变化趋势吗?提出问题:(1)这个表中,涉及哪几个变量?(2)这些变量的范围分别是多少?列表法问题情境2、一物体从静止开始下落,下落的距离y(单位:m)与下 落的时间x(单位:s)之间近似地满足关系式y=4.9x2 , 若一物体下落2s,你能求出它下落的距离吗?解析法提出问题:(1)这个表中,涉及哪几个变量?(2)这些变量的范围分别是多少?问题情境3、下图为某市一天24小时内的气温变化图,试根据下图 回答下列问题:(1)上午6时的气温约是多少?全天的最高、最低气温 分别是多少?(2)在什么时刻,气温为0oC?(3)在什么时段内,气温在0oC以上?图象法提出问题:(1)这个表中,涉及哪几个变量?(2)这些变量的范围分别是多少?数学分析每个问题均涉及两个非空数集A,B。数学分析存在某种对应法则,对于A中任意元素x,B中总有唯一元素y与之对应。提出问题:如何利用集合的观点来描述函数呢?数学建构1、函数的概念一般地,给定两个非空实数集合A和B,如果按照某种对应关系f,对于集合A中的每一个实数x,在集合B中都有唯一的实数y和它对应,那么就称f: A→B为从集合A到集合B的一个函数(function),记作 y= f (x),x∈A其中x叫做自变量,集合A叫做函数的定义域(domain)。数学建构2、函数的定义域和值域的概念在函数y= f (x),x∈A中,x叫做自变量,所有输入值x构成的集合A叫做函数的定义域(domain);如果对于集合A中的每一个x (输入值),都有一个y(输出值)与之对应,我们将所有输出值y组成的集合{y|y= f (x),x∈A}称为函数的值域(range)。数学探究结论:函数值域是集合B的子集。 思考:函数的值域是集合B吗?若不是,两者之间有什么 关系?数学建构3、函数的三要素(1)定义域;(2)对应法则;(3)值域。4、函数常见的表示方法(1)列表法;(2)图象法;(3)解析法。数学建构5、初中所学常见的函数定义域和值域(3)一次函数:y = kx+b(k≠0);(4)二次函数:y = ax2+bx+c (a≠0)。(1)正比例函数:y = kx (k≠0);数学应用类型 函数概念的理解问题:若是集合A 到 B的函数,则函数的定义域和 值域分别是什么?数学练习判断下列对应是否为函数:(1)x→y=x,x∈{x|0≤x≤6},y∈{y|0≤y≤3};(2) ,x∈{x|0≤x≤6},y∈{y|0≤y≤3};(3)x→y=3x+1,x∈R,y∈R。数学练习判断下列对应f是否为从集合A到集合B的函数。 数学应用数学练习课堂检测课本第100~101页第1、2、3、4题。生活趣味解答: 集合A里是全世界所有的人,集合B里是全世界所有的男人,对应法则就是找father,A里的元素都能在B中找到父亲,不同的人可能有相同的父亲,但是一个人不会出现两个父亲,还有一些男人没人管他叫父亲。1、函数的概念一般地,给定两个非空实数集合A和B,如果按照某种对应关系f,对于集合A中的每一个实数x,在集合B中都有唯一的实数y和它对应,那么就称f: A→B为从集合A到集合B的一个函数(function),记作 y= f (x),x∈A其中x叫做自变量,集合A叫做函数的定义域(domain)。2、函数的定义域和值域的概念在函数y= f (x),x∈A中,x叫做自变量,所有输入值x构成的集合A叫做函数的定义域(domain);如果对于集合A中的每一个x (输入值),都有一个y(输出值)与之对应,我们将所有输出值y组成的集合{y|y= f (x),x∈A}称为函数的值域(range)。课堂小结3、函数的三要素(1)定义域;(2)对应法则;(3)值域。4、函数常见的表示方法(1)列表法;(2)图象法;(3)解析法。课堂小结
函数的概念(1)课前导入我们的生活的世界时刻都在发生变化,变化无处不在。这些变化着的现象都可以用数学来有效地描述。函数是描述客观世界变化规律的重要数学模型,函数模型可以帮助我们解决许多实际问题。因此,学习函数知识对研究客观世界、掌握事物变化规律具有重要的意义。函数是本章的核心概念,也是中学数学中的基本概念。高中阶段不仅把函数看成变量之间的依赖关系,同时还用集合与对应的语言刻画函数,函数的思想将贯穿整个高中数学课程。复习回顾1、初中学过的函数的概念如何表述一般地,如果在一个变化过程中,有两个 变量 x和y,对于x的每一个值, y都有唯一的 值与之对应,我们就说y是x的函数,x是自变量。2、常用的表示函数关系的方法(1)解析法;(2)列表法;(3)图象法。复习回顾3、初中所学常见的函数模型(3)一次函数的一般形式为:y = kx+b(k≠0);(4)二次函数的一般形式:y = ax2+bx+c (a、b、c 是常数 ,a≠0)。(1)正比例函数的一般形式为:y = kx (k≠0);问题情境1、人口数量变化趋势是我们制定一系列相关政策的 依据, 从中国的统计年鉴中可以查得我国1979~2014年人口数 据资料(年末)如下表所示,你能根据该表说出我国人口 的变化趋势吗?提出问题:(1)这个表中,涉及哪几个变量?(2)这些变量的范围分别是多少?列表法问题情境2、一物体从静止开始下落,下落的距离y(单位:m)与下 落的时间x(单位:s)之间近似地满足关系式y=4.9x2 , 若一物体下落2s,你能求出它下落的距离吗?解析法提出问题:(1)这个表中,涉及哪几个变量?(2)这些变量的范围分别是多少?问题情境3、下图为某市一天24小时内的气温变化图,试根据下图 回答下列问题:(1)上午6时的气温约是多少?全天的最高、最低气温 分别是多少?(2)在什么时刻,气温为0oC?(3)在什么时段内,气温在0oC以上?图象法提出问题:(1)这个表中,涉及哪几个变量?(2)这些变量的范围分别是多少?数学分析每个问题均涉及两个非空数集A,B。数学分析存在某种对应法则,对于A中任意元素x,B中总有唯一元素y与之对应。提出问题:如何利用集合的观点来描述函数呢?数学建构1、函数的概念一般地,给定两个非空实数集合A和B,如果按照某种对应关系f,对于集合A中的每一个实数x,在集合B中都有唯一的实数y和它对应,那么就称f: A→B为从集合A到集合B的一个函数(function),记作 y= f (x),x∈A其中x叫做自变量,集合A叫做函数的定义域(domain)。数学建构2、函数的定义域和值域的概念在函数y= f (x),x∈A中,x叫做自变量,所有输入值x构成的集合A叫做函数的定义域(domain);如果对于集合A中的每一个x (输入值),都有一个y(输出值)与之对应,我们将所有输出值y组成的集合{y|y= f (x),x∈A}称为函数的值域(range)。数学探究结论:函数值域是集合B的子集。 思考:函数的值域是集合B吗?若不是,两者之间有什么 关系?数学建构3、函数的三要素(1)定义域;(2)对应法则;(3)值域。4、函数常见的表示方法(1)列表法;(2)图象法;(3)解析法。数学建构5、初中所学常见的函数定义域和值域(3)一次函数:y = kx+b(k≠0);(4)二次函数:y = ax2+bx+c (a≠0)。(1)正比例函数:y = kx (k≠0);数学应用类型 函数概念的理解问题:若是集合A 到 B的函数,则函数的定义域和 值域分别是什么?数学练习判断下列对应是否为函数:(1)x→y=x,x∈{x|0≤x≤6},y∈{y|0≤y≤3};(2) ,x∈{x|0≤x≤6},y∈{y|0≤y≤3};(3)x→y=3x+1,x∈R,y∈R。数学练习判断下列对应f是否为从集合A到集合B的函数。 数学应用数学练习课堂检测课本第100~101页第1、2、3、4题。生活趣味解答: 集合A里是全世界所有的人,集合B里是全世界所有的男人,对应法则就是找father,A里的元素都能在B中找到父亲,不同的人可能有相同的父亲,但是一个人不会出现两个父亲,还有一些男人没人管他叫父亲。1、函数的概念一般地,给定两个非空实数集合A和B,如果按照某种对应关系f,对于集合A中的每一个实数x,在集合B中都有唯一的实数y和它对应,那么就称f: A→B为从集合A到集合B的一个函数(function),记作 y= f (x),x∈A其中x叫做自变量,集合A叫做函数的定义域(domain)。2、函数的定义域和值域的概念在函数y= f (x),x∈A中,x叫做自变量,所有输入值x构成的集合A叫做函数的定义域(domain);如果对于集合A中的每一个x (输入值),都有一个y(输出值)与之对应,我们将所有输出值y组成的集合{y|y= f (x),x∈A}称为函数的值域(range)。课堂小结3、函数的三要素(1)定义域;(2)对应法则;(3)值域。4、函数常见的表示方法(1)列表法;(2)图象法;(3)解析法。课堂小结
相关资料
更多









