第二章 一元一次不等式和一元一次不等式组单元小结 课件PPT

这是一份第二章 一元一次不等式和一元一次不等式组单元小结 课件PPT，共28页。
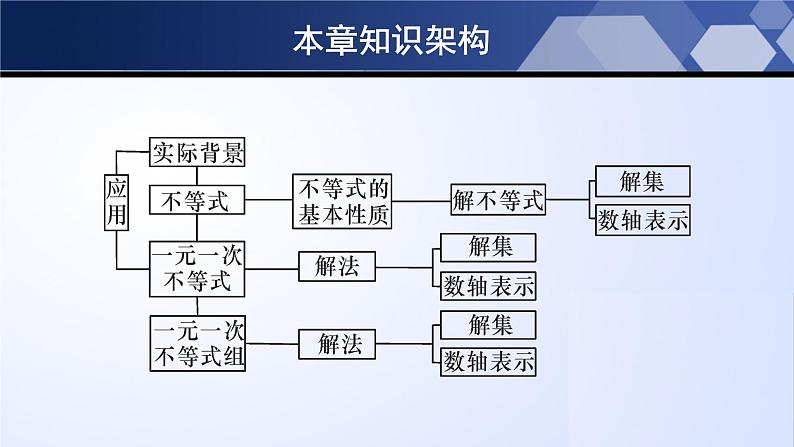
新课标 北师大版八年级下册 第二章 一元一次不等式和一元一次不等式组单元小结本章知识架构知识专题知识点一：概念学习概念一：不等式 定义：一般地，用符号“＜”(或“≤”)，“＞” (或“≥”)，“≠”连接的式子叫做不等式.知识专题 概念二：一元一次不等式 左右两边都是整式，只含有一个未知数，并且未知数的最高次数是1的不等式，叫做一元一次不等式.特点：(1)左右两边都是整式;(2)只含有一个未知数;(3)未知数的最高次数是1.知识专题 概念3：一元一次不等式组 一般地，关于同一未知数的几个一元一次不等式合在一起，就组成一个一元一次不等式组.条件: (1)同一未知数（只有一种字母）;(2)一元一次不等式.知识专题 概念4：不等式(组 )的解或解集 能使不等式成立的未知数的解，叫做不等式的解.(1)一个含有未知数的不等式的所有解，组成这个不等式的解集；(2)不等式组中各个不等式的解集的公共部分叫做不等式组的解集；知识专题 概念4：不等式(组 )的解或解集 在数轴上表示解集“＞”或“＜”画空心圆圈，表示不包括某点“≥”或“≤”画实心圆点，表示包括某点 大于向右画，小于向左画.知识专题知识点二：不等式的基本性质1.不等式的两边都加（或减）同一个整式，不等号的方向不变.2.不等式的两边都乘(或除以)同一个正数，不等号的方向不变.3.不等式的两边都乘(或除以)同一个负数，不等号的方向改变。知识专题知识点三：解法（一）一元一次不等式的解法解一元一次不等式的步骤：（1）去分母； （2）去括号； （3）移项；（4）合并同类项；（5）系数化1。知识专题注意:(1)去分母时,不要漏乘常数项,分子是多项式时要加括号；(2)移项时，要变号；(3)系数化为1时,不等式的两边都乘或除以同一个负数,不等号的方向要改变.知识专题（二）一元一次不等式组的解法 解一元一次不等式组的步骤：（1）求不等式组中各个不等式的解集；（2）利用数轴，找出不等式解集的公共部分；（3）写出不等式组的解集。知识专题一元一次不等式组的解集的确定方法有两种：①利用数轴，②利用口诀，如下表所示：知识专题知识点四：应用（一）一元一次不等式的应用（二）一元一次不等式组的应用解题步骤：审、设、列、解、验、答关键字：“至少”、“不低于”、“不超过”、“最多”知识专题（三）一元一次不等式组与一次函数的应用一元一次不等式kx+b>0与一次函数y=kx+b的联系：知识专题（三）一元一次不等式组与一次函数的应用一元一次不等式kx+b>0与一次函数y=kx+b的联系：ax+b>cx+d(或ax+by2(或y1cx+d（或ax+b-1,则下列各式错误的是　(　　)A.3x>-3　 B.-2x0 D.1-x>2【解析】由不等式性质2知,A正确; 由性质3知,B正确;由性质1知,C正确;在x>-1两边同乘-1,得-x