

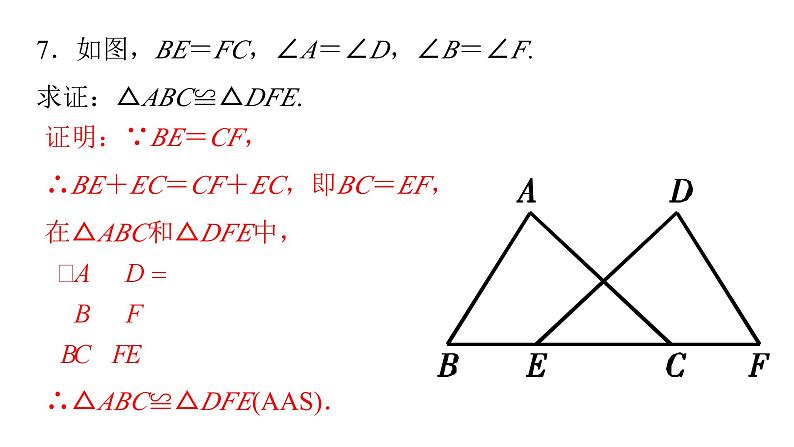
- 七年级数学下册方程思想习题课件-(北师大) 课件 0 次下载
- 七年级数学下册代数计算课件-(北师大) 课件 0 次下载
- 七年级数学下册期末复习-(北师大)课件PPT 课件 0 次下载
- 七年级数学下册期末复习课件-(北师大) 课件 0 次下载
- 七年级数学下册习题课件辅助线作法 课件 0 次下载
七年级数学下册几何证明课件-(北师大)
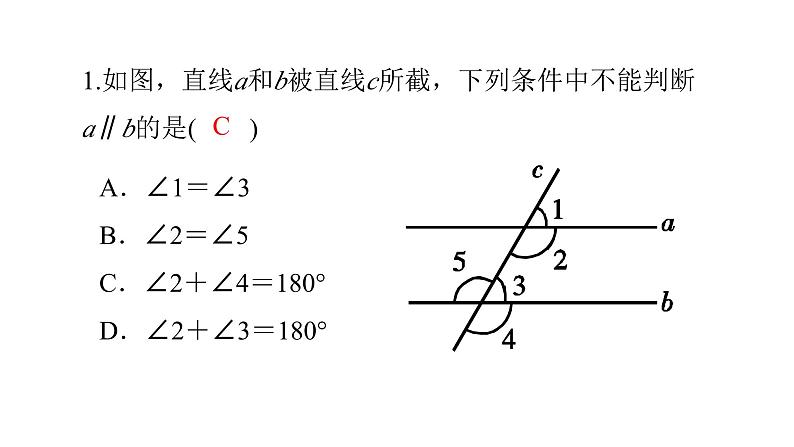
展开1.如图,直线a和b被直线c所截,下列条件中不能判断a∥b的是( )
A.∠1=∠3B.∠2=∠5C.∠2+∠4=180°D.∠2+∠3=180°
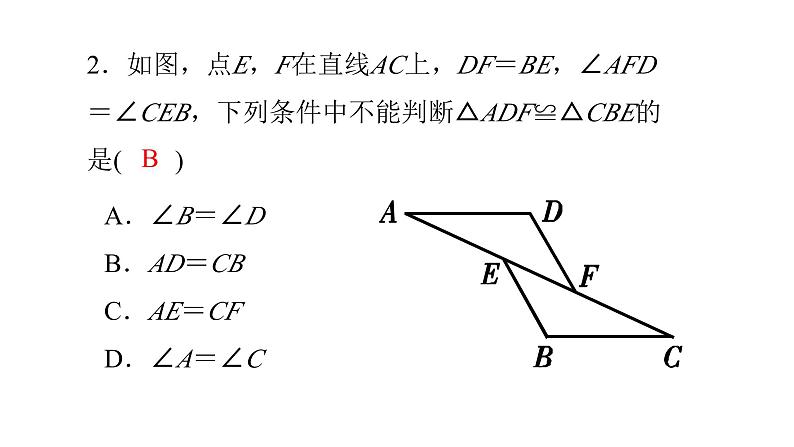
2.如图,点E,F在直线AC上,DF=BE,∠AFD=∠CEB,下列条件中不能判断△ADF≌△CBE的是( )
A.∠B=∠DB.AD=CBC.AE=CFD.∠A=∠C
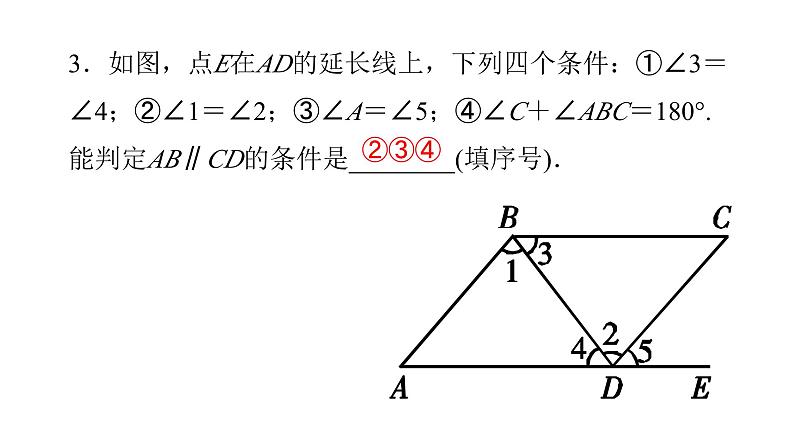
3.如图,点E在AD的延长线上,下列四个条件:①∠3=∠4;②∠1=∠2;③∠A=∠5;④∠C+∠ABC=180°.能判定AB∥CD的条件是________(填序号).
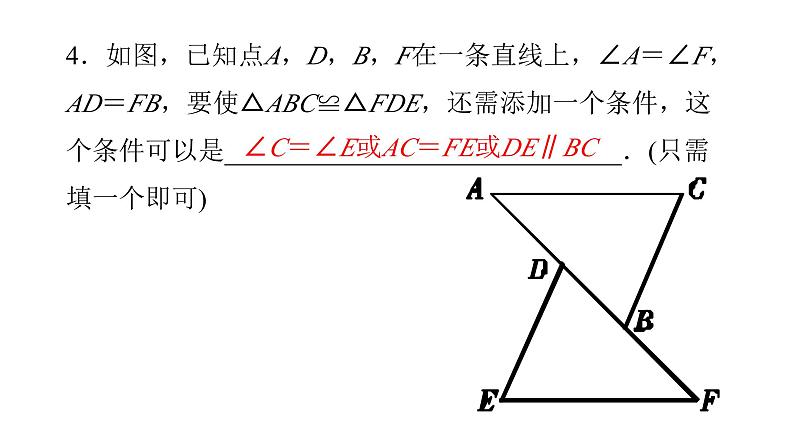
4.如图,已知点A,D,B,F在一条直线上,∠A=∠F,AD=FB,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是______________________________.(只需填一个即可)
∠C=∠E或AC=FE或DE∥BC
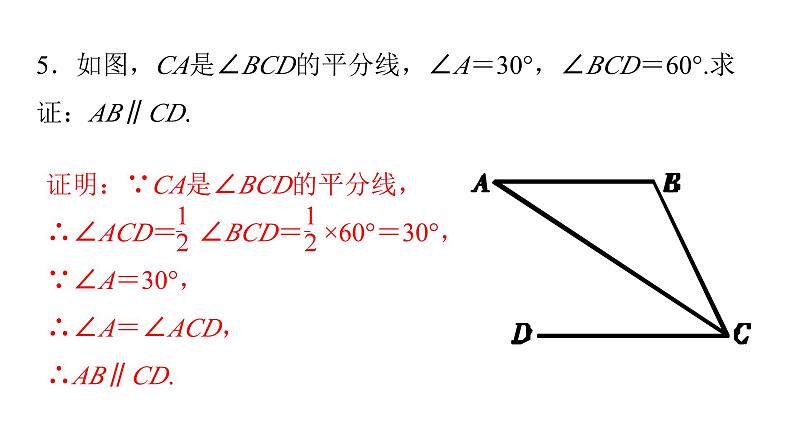
5.如图,CA是∠BCD的平分线,∠A=30°,∠BCD=60°.求证:AB∥CD.
6.如图,∠1=53°,∠2=127°,∠3=53°,试说明直线AB与CD,BC与DE的位置关系.
解:AB∥DC,BC∥DE,理由:∵∠1=53°,∠3=53°,∴∠1=∠3,∴BC∥DE,∵∠2=127°,∴∠4=53°,∴∠4=∠3,∴AB∥CD.
7.如图,BE=FC,∠A=∠D,∠B=∠F.求证:△ABC≌△DFE.
证明:∵BE=CF,∴BE+EC=CF+EC,即BC=EF,在△ABC和△DFE中,∴△ABC≌△DFE(AAS).
8.如图,BD⊥AC于点D,CE⊥AB于点E,BD与CE相交于点O,连接线段AO,AO恰好平分∠BAC.求证:OB=OC.
9.如图,△ABC和△CDE均为等腰三角形,AC=BC,CD=CE,∠ACB=∠DCE,点D在线段AB上(与A,B不重合),连接BE.(1)证明:△ACD≌△BCE;(2)若BD=2,BE=5,求AB的长.
(2)解:由(1)知:△ACD≌△BCE,∴AD=BE=5,∴AB=AD+BD=5+2=7.
10.如图,在△ABC中,AD⊥BC于点D,E为AC上一点,连接BE交AD于F,且AD=BD,DC=DF.求证:BE⊥AC.
11.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE,BE,延长AE交BC的延长线于点F.(1)求证:△DAE≌△CFE;(2)若AB=BC+AD,求证:BE⊥AF.
(2)由(1)知△DAE≌△CFE,∴AE=EF,AD=CF,∵AB=BC+AD,∴AB=BC+CF,即AB=BF,在△ABF中,∵AE=EF,∴∠AEB=∠FEB=90°(三线合一),∴BE⊥AE;
12.如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分∠CAB交CE于点F,DF的延长线交AC于点G.求证:(1)DF∥BC; (2)FG=FE.
(2)∵DF∥BC,BC⊥AC,∴FG⊥AC.∵FE⊥AB,又AF平分∠CAB,∴FG=FE.
13.如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是BC的中点,CE⊥AD,垂足为点E,BF∥AC交CE的延长线于点F.求证:AC=2BF.
14.(1)如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,E,求证:DE=BD+CE;(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明;若不成立,请说明理由.
青岛版八年级上册5.6 几何证明举例完整版课件ppt: 这是一份青岛版八年级上册5.6 几何证明举例完整版课件ppt,共14页。PPT课件主要包含了学习目标,∴PMPN,通过证明我们得到,典例精析,当堂小练,课后作业,完成练习等内容,欢迎下载使用。
初中数学第5章 几何证明初步5.6 几何证明举例精品习题课件ppt: 这是一份初中数学第5章 几何证明初步5.6 几何证明举例精品习题课件ppt,文件包含《几何证明举例》课件ppt、练习1_几何证明举例ppt、练习2_几何证明举例ppt、练习3_几何证明举例ppt、练习4_几何证明举例ppt、练习5_几何证明举例ppt、《几何证明举例》习题doc、例题_几何证明举例ppt、导入_几何证明举例ppt、等腰三角形拓展练习_几何证明举例ppt、《几何证明举例》教案doc等11份课件配套教学资源,其中PPT共29页, 欢迎下载使用。
初中数学青岛版八年级上册第5章 几何证明初步5.3 什么是几何证明试讲课习题ppt课件: 这是一份初中数学青岛版八年级上册第5章 几何证明初步5.3 什么是几何证明试讲课习题ppt课件,文件包含《什么是几何证明》课件ppt、巩固练习_命题与证明ppt、拓展练习_什么是几何证明ppt、练习_什么是几何证明ppt、《什么是几何证明》习题doc、做一做_命题与证明ppt、《什么是几何证明》教案doc等7份课件配套教学资源,其中PPT共17页, 欢迎下载使用。













