




还剩6页未读,
继续阅读
所属成套资源:2024北师大版七年级下册数学整册课件多份
成套系列资料,整套一键下载
2024七下数学极速提分法第13招线段垂直平分线与角平分线的应用类型课件(北师大版)
展开
这是一份2024七下数学极速提分法第13招线段垂直平分线与角平分线的应用类型课件(北师大版),共12页。
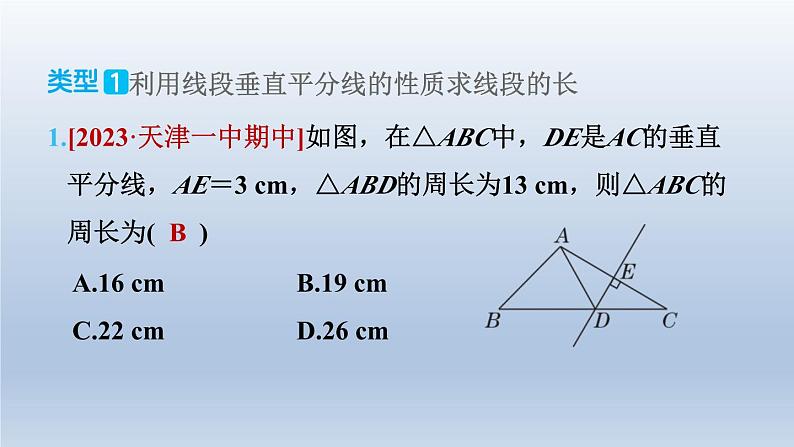
北师版七年级下第13招 线段垂直平分线与角平分线的应用类型除了等腰三角形之外,还有两类特殊的轴对称图形——线段和角,灵活运用它们轴对称的性质不仅可以求线段的长度、角的度数,说明数量关系等,还可以解决实际生活中的问题. 在BD上截取BE',使BE'=CE,连接CE'.利用线段垂直平分线的性质和“边角边”说明△BPE和△CPE'全等,为说明BE=CD创造条件.解:如图,在BD上截取BE',使BE'=CE.因为PG为BC的垂直平分线,所以PB=PC.所以∠PBC=∠PCB,PE'=PE.又因为∠BPE=∠CPE',所以△BPE≌△CPE'(SAS).所以BE=CE',∠EBP=∠E'CP.因为∠CDE'=180°-∠ADB=∠A+∠ABP,∠CE'D=180°-∠CE'B=∠E'BC+∠BCE'=2∠PBC+∠E'CP=∠A+∠E'CP,所以∠CDE'=∠CE'D.易得CD=CE'.所以BE=CD. 利用线段垂直平分线的性质求线段的长1.[2023·天津一中期中]如图,在△ABC中,DE是AC的垂直 平分线,AE=3 cm,△ABD的周长为13 cm,则△ABC的 周长为( B )B 利用线段垂直平分线的性质求角的度数2.[2023·北京四中月考]如图,在△ABC中,∠A=36°,AB= AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接 BD,下列结论错误的是( D )D【点拨】因为∠A=36°,AB=AC,所以∠C=∠ABC=72°.所以 ∠C=2∠A,故选项A正确.因为OD是AB的垂直平分线,所 以AD=BD.所以∠ABD=∠A=36°.所以∠DBC=72°-36°= 36°=∠ABD.所以BD是∠ABC的平分线,故选项B正确.由 A,B选项可以知道△ABC,△BDC,△ADB是等腰三角 形,故选项C正确.根据已知不能推出△BCD的面积和△BOD 的面积相等,故选项D错误. 利用线段垂直平分线的性质解决实际问题3.如图,某城市规划局为了方便居民的生活,计划在三个住 宅小区A,B,C之间修建一个购物中心,试问:该购物中 心应建于何处,才能使得它到三个小区的距离相等?【解】如图,连接AB,BC,分别作AB,BC的垂直平分线 DE,GF,两直线交于点M,则点M就是所要确定的购物中 心的位置.【点拨】解决作图选点类问题,若要找到某两个点的距离相等的 点,一般在这两点所连线段的垂直平分线上去找;若要找到 某两条不平行的直线的距离相等的点,一般在这两条直线相 交所成的角的平分线上去找. 利用角平分线的性质说明线段的位置关系4.已知:如图,AD为△ABC的角平分线,DE⊥AC于点E, DF⊥AB于点F,EF交AD于点M.试说明:AD垂直平分EF. (提示:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上)【解】如图,因为AD为△ABC的角平分线,DE⊥AC, DF⊥AB,所以DE=DF.所以点D在EF的垂直平分线上. 所以△AFD≌△AED(AAS).所以AF=AE.所以点A在EF的垂直平分线上.所以AD垂直平分EF.
北师版七年级下第13招 线段垂直平分线与角平分线的应用类型除了等腰三角形之外,还有两类特殊的轴对称图形——线段和角,灵活运用它们轴对称的性质不仅可以求线段的长度、角的度数,说明数量关系等,还可以解决实际生活中的问题. 在BD上截取BE',使BE'=CE,连接CE'.利用线段垂直平分线的性质和“边角边”说明△BPE和△CPE'全等,为说明BE=CD创造条件.解:如图,在BD上截取BE',使BE'=CE.因为PG为BC的垂直平分线,所以PB=PC.所以∠PBC=∠PCB,PE'=PE.又因为∠BPE=∠CPE',所以△BPE≌△CPE'(SAS).所以BE=CE',∠EBP=∠E'CP.因为∠CDE'=180°-∠ADB=∠A+∠ABP,∠CE'D=180°-∠CE'B=∠E'BC+∠BCE'=2∠PBC+∠E'CP=∠A+∠E'CP,所以∠CDE'=∠CE'D.易得CD=CE'.所以BE=CD. 利用线段垂直平分线的性质求线段的长1.[2023·天津一中期中]如图,在△ABC中,DE是AC的垂直 平分线,AE=3 cm,△ABD的周长为13 cm,则△ABC的 周长为( B )B 利用线段垂直平分线的性质求角的度数2.[2023·北京四中月考]如图,在△ABC中,∠A=36°,AB= AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接 BD,下列结论错误的是( D )D【点拨】因为∠A=36°,AB=AC,所以∠C=∠ABC=72°.所以 ∠C=2∠A,故选项A正确.因为OD是AB的垂直平分线,所 以AD=BD.所以∠ABD=∠A=36°.所以∠DBC=72°-36°= 36°=∠ABD.所以BD是∠ABC的平分线,故选项B正确.由 A,B选项可以知道△ABC,△BDC,△ADB是等腰三角 形,故选项C正确.根据已知不能推出△BCD的面积和△BOD 的面积相等,故选项D错误. 利用线段垂直平分线的性质解决实际问题3.如图,某城市规划局为了方便居民的生活,计划在三个住 宅小区A,B,C之间修建一个购物中心,试问:该购物中 心应建于何处,才能使得它到三个小区的距离相等?【解】如图,连接AB,BC,分别作AB,BC的垂直平分线 DE,GF,两直线交于点M,则点M就是所要确定的购物中 心的位置.【点拨】解决作图选点类问题,若要找到某两个点的距离相等的 点,一般在这两点所连线段的垂直平分线上去找;若要找到 某两条不平行的直线的距离相等的点,一般在这两条直线相 交所成的角的平分线上去找. 利用角平分线的性质说明线段的位置关系4.已知:如图,AD为△ABC的角平分线,DE⊥AC于点E, DF⊥AB于点F,EF交AD于点M.试说明:AD垂直平分EF. (提示:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上)【解】如图,因为AD为△ABC的角平分线,DE⊥AC, DF⊥AB,所以DE=DF.所以点D在EF的垂直平分线上. 所以△AFD≌△AED(AAS).所以AF=AE.所以点A在EF的垂直平分线上.所以AD垂直平分EF.
相关资料
更多









