



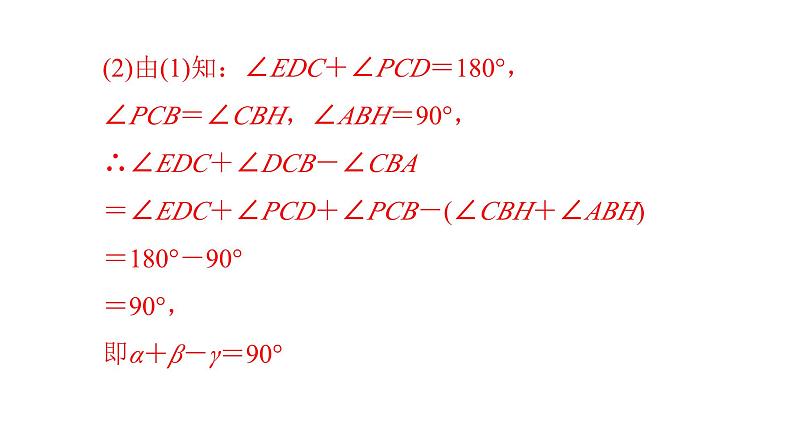
- 七年级数学下册期末复习-(北师大)课件PPT 课件 0 次下载
- 七年级数学下册期末复习课件-(北师大) 课件 0 次下载
- 七年级数学下册习题课件几何计算-(北师大) 课件 0 次下载
- 七年级数学下册新定义运算-(北师大)课件PPT 课件 0 次下载
- 七年级数学下册阅读理解习题课件-(北师大) 课件 1 次下载
七年级数学下册习题课件辅助线作法
展开一、添加平行线,利用平行线性质1.如图,∠BED=∠B+∠D,猜想AB与CD有怎样的位置关系,并说明理由.
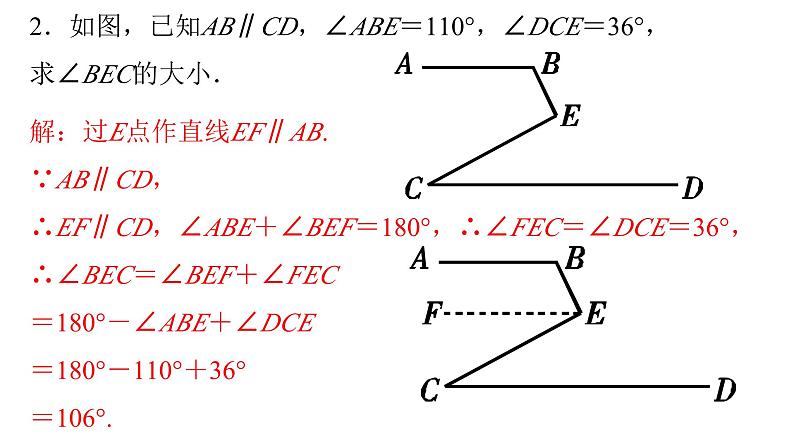
2.如图,已知AB∥CD,∠ABE=110°,∠DCE=36°,求∠BEC的大小.
3.如图为一台灯示意图,其中灯头连接杆DE始终和桌面FG平行,灯脚AB始终和桌面FG垂直,(1)当∠EDC=∠DCB=120°时,求∠CBA;(2)连杆BC,CD可以绕着B,C和D进行旋转,灯头E始终在D左侧,设∠EDC,∠DCB,∠CBA的度数分别为α,β,γ,求α,β,γ之间的数量关系.
(2)由(1)知:∠EDC+∠PCD=180°,∠PCB=∠CBH,∠ABH=90°,∴∠EDC+∠DCB-∠CBA=∠EDC+∠PCD+∠PCB-(∠CBH+∠ABH)=180°-90°=90°,即α+β-γ=90°
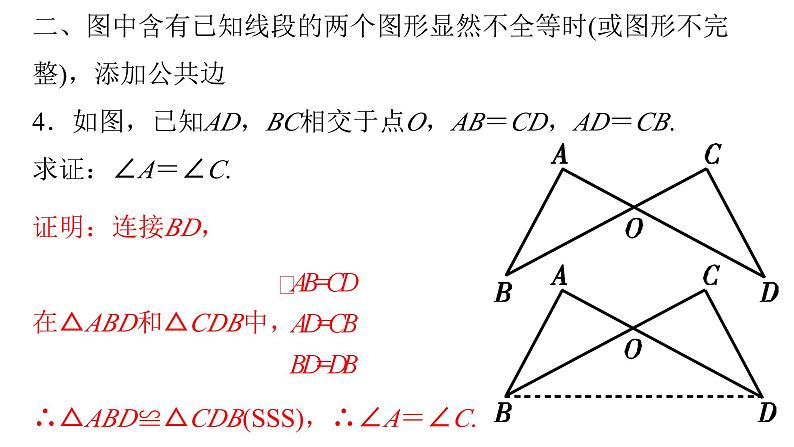
二、图中含有已知线段的两个图形显然不全等时(或图形不完整),添加公共边4.如图,已知AD,BC相交于点O,AB=CD,AD=CB.求证:∠A=∠C.
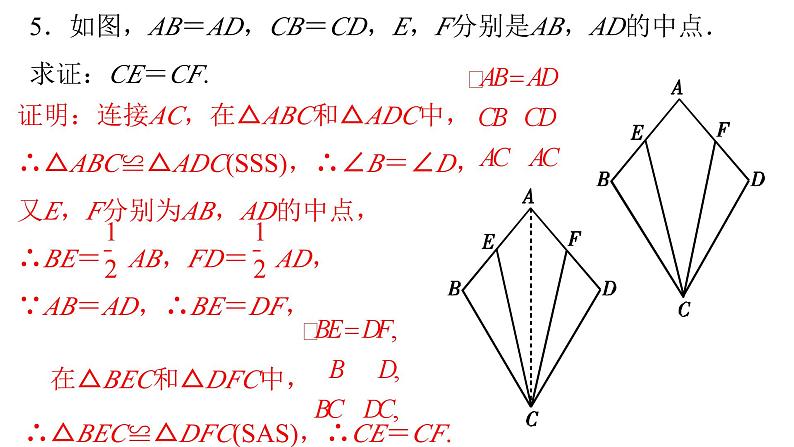
5.如图,AB=AD,CB=CD,E,F分别是AB,AD的中点.求证:CE=CF.
三、遇到等腰三角形,可作底边上的高或延长加倍法(三线合一或对折)6.如图,在△ABC中,AB=AC,BD⊥AC,垂足为D.求证:∠BAC =2∠CBD.
7.如图,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,BD平分∠ABC交AC于点D,CE垂直于BD,交BD的延长线于点E,求证:BD=2CE.
四、截长补短:一般地,当所证结论为线段的和、差关系,且这两条线段不在同一直线上时,通常可以考虑用截长补短的办法:或在长线段上截取一部分使之与短线段相等;或将短线段延长使其与长线段相等
8.如图,AD∥BC,点E在线段AB上,∠ADE=∠CDE,∠DCE=∠ECB.求证:CD=AD+BC.
9.如图,在△ABC中,∠ABC=60°,AD,CE分别平分∠BAC,∠ACB,求证:AC=AE+CD.
中考数学复习方法技巧突破(七)圆中常见辅助线的作法教学课件: 这是一份中考数学复习方法技巧突破(七)圆中常见辅助线的作法教学课件,共10页。
中考数学复习方法技巧突破(七)圆中常见辅助线的作法作业课件: 这是一份中考数学复习方法技巧突破(七)圆中常见辅助线的作法作业课件,共9页。
2023年中考数学专项复习课件:与中点有关的辅助线作法: 这是一份2023年中考数学专项复习课件:与中点有关的辅助线作法,共22页。PPT课件主要包含了构造中位线,方法解读,第1题图,第2题图,第3题图,第4题图,构造中线,第5题图,第6题图,第7题图等内容,欢迎下载使用。














