2023高考数学二轮专题复习与测试专题强化练八概率与统计

这是一份2023高考数学二轮专题复习与测试专题强化练八概率与统计，共10页。试卷主要包含了深圳是一座志愿者之城、爱心之城，在新的高考改革方案中规定，下列说法正确的是等内容，欢迎下载使用。
专题强化练(八)　概率与统计
1．(2022·佛山模拟)小明上学可以乘坐公共汽车，也可以乘坐地铁．已知小明上学乘坐公共汽车的概率为0.4，乘坐地铁的概率为0.6，而且乘坐公共汽车与地铁时，小明迟到的概率分别为0.05和0.04，则小明准时到校的概率为(　　)
A．0.954　　　　　　　　 B．0.956
C．0.958 D．0.959
解析：小明上学乘坐公共汽车准时到校的概率为0.4×(1－0.05)＝0.38，
小明上学乘坐地铁准时到校的概率为0.6×(1－0.04)＝0.576，
所以小明准时到校的概率为0.38＋0.576＝0.956.
故选B.
答案：B
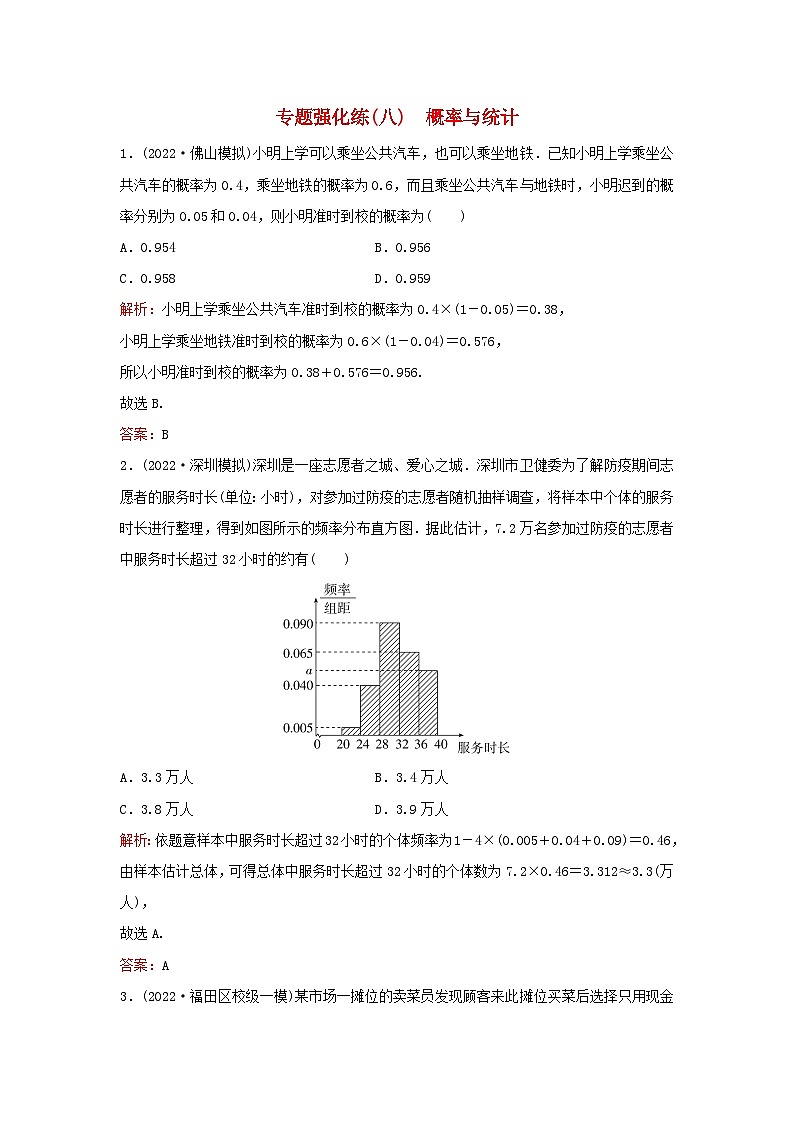
2．(2022·深圳模拟)深圳是一座志愿者之城、爱心之城．深圳市卫健委为了解防疫期间志愿者的服务时长(单位：小时)，对参加过防疫的志愿者随机抽样调查，将样本中个体的服务时长进行整理，得到如图所示的频率分布直方图．据此估计，7.2万名参加过防疫的志愿者中服务时长超过32小时的约有(　　)

A．3.3万人 B．3.4万人
C．3.8万人 D．3.9万人
解析：依题意样本中服务时长超过32小时的个体频率为1－4×(0.005＋0.04＋0.09)＝0.46，
由样本估计总体，可得总体中服务时长超过32小时的个体数为7.2×0.46＝3.312≈3.3(万人)，
故选A.
答案：A
3．(2022·福田区校级一模)某市场一摊位的卖菜员发现顾客来此摊位买菜后选择只用现金支付的概率为0.2，选择既用现金支付又用非现金支付的概率为0.1，且买菜后无赊账行为，则选择只用非现金支付的概率为(　　)
A．0.5 B．0.6
C．0.7 D．0.8
解析：设事件A为只用现金支付，事件B为只用非现金支付，事件C为既用现金支付又用非现金支付，事件D为买菜后支付，
则P(D)＝P(A)＋P(B)＋P(C)＝1，
因为P(A)＝0.2，P(C)＝0.1，
所以P(B)＝0.7.
故选C.
答案：C
4．(2022·汕头一模)有4名大学生志愿者参加2022年北京冬奥会志愿服务．冬奥会志愿者指挥部随机派这4名志愿者参加冰壶、短道速滑、花样滑冰3个项目比赛的志愿服务，则每个项目至少安排一名志愿者进行志愿服务的概率(　　)
A. B.
C. D.
解析：先将4人分成3组，其中一组有2人，另外一组各1人，共有C＝6(种)，然后将3个项目全排列，共有A＝6(种)排法，
故每个项目至少安排一名志愿者进行志愿服务的方法数为6×6＝36(种)，
因为4名志愿者参加3个项目比赛的志愿者服务的总方法数34＝81(种)，
所以每个项目至少安排一名志愿者进行志愿服务的概率P＝＝.
故选D.
答案：D
5．(2022·潮州二模)围棋盒子中有多粒黑子和白子，已知从中取出2粒都是黑子的概率为，都是白子的概率是，则从中任意取出2粒恰好是不同色的概率是(　　)
A. B.
C. D.
解析：围棋盒子中有多粒黑子和白子，
因为从中取出2粒都是黑子的概率为，都是白子的概率是，
所以由对立事件概率计算公式得：
从中任意取出2粒恰好是不同色的概率是：
P＝1－－＝.
故选D.
答案：D
6．(2022·揭阳模拟)在新的高考改革方案中规定：每位考生的高考成绩是按照3(语文、数学、英语)＋2(物理、历史)选1＋4(化学、生物、地理、政治)选2的模式设置的，则在选考的科目中甲、乙两位同学恰有两科相同的概率为(　　)
A. B.
C. D.
解析：在选考的科目中甲、乙两位同学选考的基本事件总数n＝CC·CC＝144，其中甲、乙两位同学恰有两科相同包含的基本事件个数：
m＝CC·CCC＋CC·CC＝60，
所以在选考的科目中甲、乙两位同学恰有两科相同的概率为P＝＝＝.
故选C.
答案：C
7．(2022·晋城三模)数据x1，x2，x3，…，xm的平均数为，数据y1，y2，y3，…，yn的平均数为，则数据x1，x2，x3，…，xm，y1，y2，y3，…，yn的平均数为(　　)
A.＋ B.＋
C. D.
解析：因为数据x1，x2，x3，…，xm的平均数为，数据y1，y2，y3，…，yn的平均数为，所以数据x1，x2，x3，…，xm，y1，y2，y3，…，yn的平均数为[(x1＋x2＋x3＋…＋xm)＋(y1＋y2＋y3＋…＋yn)]＝[m＋n]＝.
故选D.
答案：D
8．(多选题)(2022·湛江二模)某学校组建了合唱、朗诵、脱口秀、舞蹈、太极拳五个社团，该校共有2 000名同学，每名同学依据自己兴趣爱好最多可参加其中一个，各个社团的人数比例的饼状图如图所示，其中参加朗诵社团的同学有8名，参加太极拳社团的有12名，则(　　)

A．这五个社团的总人数为100
B．脱口秀社团的人数占五个社团总人数的20%
C．这五个社团总人数占该校学生人数的4%
D．从这五个社团中任选一人，其来自脱口秀社团或舞蹈社团的概率为40%
解析：由于参加朗诵社团的同学有8名，该社团人数占比为10%，所以社团总人数为80人，故A错误；合唱团人数为80×30%＝24，舞蹈社团人数为80×25%＝20(人)，所以脱口秀社团的人数为80－24－12－20－8＝16，所以脱口秀社团的人数占有五个社团总人数的＝20%，故B正确；五个社团总人数占该校学生人数的＝4%，故C正确；脱口秀社团的人数占五个社团总人数的20%，舞蹈社团的人数占五个社团总人数的25%，所以这两个社团人数占五个社团总人数的45%，所以从这五个社团中任选一人，其来自脱口秀社团或舞蹈社团的概率为45%，故D错误．故选BC.
答案：BC
9．(多选题)(2022·湖南模拟)下列说法正确的是(　　)
A．为了更好地开展创文创卫工作，需要对在校中小学生参加社会实践活动的意向进行调查，拟采用分层抽样的方法从该地区A、B、C、D四个学校中抽取一个容量为400的样本进行调查，已知A、B、C、D四校人数之比为7∶4∶3∶6，则应从B校中抽取的样本数量为80
B．6件产品中有4件正品，2件次品，从中任取2件，则至少取到1件次品的概率为0.6
C．已知变量x、y线性相关，由样本数据算得线性回归方程是＝0.4x＋，且由样本数据算得＝4，＝3.7，则＝2.1
D．箱子中有4个红球、2个白球共6个小球，依次不放回地抽取2个小球，记事件M＝{第一次取到红球}，N＝{第二次取到白球}，则M、N为相互独立事件
解析：对于选项A，采用分层抽样的方法从该地区A、B、C、D四个学校中抽取一个容量为400的样本进行调查，
A、B、C、D四校人数之比为7∶4∶3∶6，
故应从B校中抽取的样本数量为400×＝80，故正确；
对于选项B，至少取到1件次品的概率为＝＝0.6，故正确；
对于选项C，因为线性回归方程是＝0.4x＋，且＝4，＝3.7，
所以＝3.7－0.4×4＝2.1，故正确；
对于选项D，M、N不是相互独立事件，故错误；
故选ABC.
答案：ABC
10．(多选题)为了解某地农村经济情况，对该地农户家庭年收入进行抽样调查，将农户家庭年收入调查数据整理得到如图频率分布直方图，根据此频率分布直方图，下面结论中正确的是(　　)

A．该地农户家庭年收入低于4.5万元的农户比率估计为6%
B．该地农户家庭年收入的中位数约为7.5万元
C．估计该地有一半以上的农户，其家庭年收入介于4.5万元至8.5万元之间
D．估计该地农户家庭年收入的平均值不超过6.5万元
解析：对于A，该地农户家庭年收入低于4.5万元的农户比率估计为(0.02＋0.04)×1＝6%，故A正确，
对于B，家庭年收入介于2.5万元至7.5万元之间的频率为0.02＋0.04＋0.1＋0.14＋0.2＝0.5，
故该地农户家庭年收入的中位数约为7.5万元，
故B正确；
对于C，家庭年收入介于4.5万元至8.5万元之间的频率为0.1＋0.14＋0.2＋0.2＝0.64>0.5，故C正确；
对于D，估计该地农户家庭年收入的平均值为
3×0.02＋4×0.04＋5×0.1＋6×0.14＋7×0.2＋8×0.2＋9×0.1＋10×0.1＋11×0.04＋12×0.02＋13×0.02＋14×0.02＝7.68>6.5，故D错误．
故选ABC.
答案：ABC
11．(多选题)(2022·广州二模)抛掷两枚质地均匀的骰子，记“第一枚骰子出现的点数小于3”为事件A，“第二枚骰子出现的点数不小于3”为事件B，则下列结论中正确的是(　　)
A．事件A与事件B互为对立事件
B．事件A与事件B相互独立
C．P(B)＝2P(A)
D．P(A)＋P(B)＝1
解析：对于A，第一枚骰子出现的点数小于3，第二枚骰子出现的点数也可能小于3，
即事件A与事件B可能同时发生，所以事件A与事件B不互斥，
所以事件A与事件B不对立，所以A不正确；
对于B，无论第一枚骰子出现的点数是否小于3，对第二枚骰子出现的点数不小于3的概率没有影响，即事件A的发生与否对事件B发生的概率没有影响，所以事件A与事件B相互独立，所以B正确；
对于C，由题知，P(A)＝＝，P(B)＝＝，
所以P(B)＝2P(A)，所以C正确；
对于D，由题知，P(A)＝＝，P(B)＝＝，
所以P(A)＋P(B)＝＋＝1，所以D正确．
故选BCD.
答案：BCD
12．(多选题)(2022·佛山模拟)为弘扬文明、和谐的社区文化氛围，更好地服务社区群众，武汉市某社区组织开展了“党员先锋”“邻里互助”两个公益服务项目，其中某个星期内两个项目的参与人数(单位：人)记录如下：
项目
星期一
星期二
星期三
星期四
星期五
星期六
星期日
党员先锋
24
27
26
25
37
76
72
邻里互助
11
13
11
11
127
132
143
对于该星期内的公益服务情况，下列说法正确的有(　　)
A．“党员先锋”项目参与人数的极差为52，中位数为25
B．“邻里互助”项目参与人数的众数为11，平均数为64
C．用频率估计概率，“党员先锋”项目连续3天参与人数不低于25的概率为
D．用频率估计概率，“邻里互助”项目连续2天参与人数不低于该项目平均数的概率为
解析：对于A，“党员先锋”项目参与人数的极差为：
76－24＝52，中位数为27，故A错误；
对于B，“邻里互助”项目参与人数的众数为11，
平均数为：(11＋13＋11＋11＋127＋132＋143)＝64，
故B正确；
对于C，用频率估计概率，“党员先锋”项目连续3天参与人数不低于25的事件设为M，
则事件M包含的基本事件有四种情况，分别为：
“星期二、星期三、星期四”，“星期三、星期四、星期五”，“星期四、星期五、星期六”，“星期五、星期六、星期日”，
其中一周内连续三天，有5种情况，分别为：
“星期一、星期二、星期三”，“星期二、星期三、星期四”，“星期三、星期四、星期五”，“星期四、星期五、星期六”，“星期五、星期六、星期日”，
所以“党员先锋”项目连续3天参与人数不低于25的概率为P(M)＝，故C错误；
对于D，用频率估计概率，“邻里互助”项目连续2天参与人数不低于该项目平均数的事件设为N，
由B知该项目平均数为64，
则事件N包含的基本事件有2种情况，分别为：
“星期五、星期六”，“星期六、星期日”，
其中一周内连续2天的情况有6种，分别为：
“星期一、星期二”，“星期二、星期三”，“星期三、星期四”，“星期四、星期五”，“星期五、星期六”，“星期六、星期日”，所以“邻里互助”项目连续2天参与人数不低于该项目平均数的概率为P(N)＝＝，故D正确．
故选BD.
答案：BD
13．(多选题)(2022·潮州二模)某旅游景点2021年1月至9月每月最低气温与最高气温(单位：℃)的折线图如图，则(　　)

A．1月到9月中，最高气温与最低气温相差最大的是4月
B．1月到9月的最高气温与月份具有比较好的线性相关关系
C．1月到9月的最高气温与最低气温的差逐步减小
D．1月到9月的最低气温的极差比最高气温的极差大
解析：由折线图知，
1月到9月中，最高气温与最低气温相差最大的是1月，
故选项A错误；
由折线图知，
1月到9月的最高气温与月份具有比较好的线性相关关系，
故选项B正确；
由折线图知，
1月到9月的最高气温与最低气温的差是摆动的，
故选项C错误；
由折线图知，
1月到9月的最低气温的极差大于25－(－10)＝35，
最高气温的极差小于35－5＝30，
故选项D正确；
故选BD.
答案：BD
14．(2022·汕头一模)在党史学习教育动员大会上，习近平总书记强调全党同志要做到学史明理、学史增信、学史崇德，学史力行．某单位对200名党员进行党史知识测试，将成绩分成6组：[70，75)，[75，80)，[80，85)，[85，90)，[90，95)，[95，100]，得到如图所示的频率分布直方图，则a＝________．

解析：由题干频率分布直方图得：
(0.025＋0.035＋0.040＋a＋0.030＋0.020)×5＝1，
解得a＝0.050.
答案：0.050
15．(2022·惠州二模)在一次教学质量调研测试中，某学校高三有1 200名学生，全部学生的数学成绩X服从正态分布N(μ，σ2)，若P(X≥100)＝0.5，且P(X≥120)＝0.2，则本次测试数学成绩在80到120之间的学生约有 ________人．
解析：因为P(X≥100)＝0.5，所以μ＝100，
所以P(80