2023高考数学二轮专题复习与测试专题强化练九统计案例

这是一份2023高考数学二轮专题复习与测试专题强化练九统计案例，共10页。试卷主要包含了规定抽球试验规则如下等内容，欢迎下载使用。
专题强化练(九)　统计案例
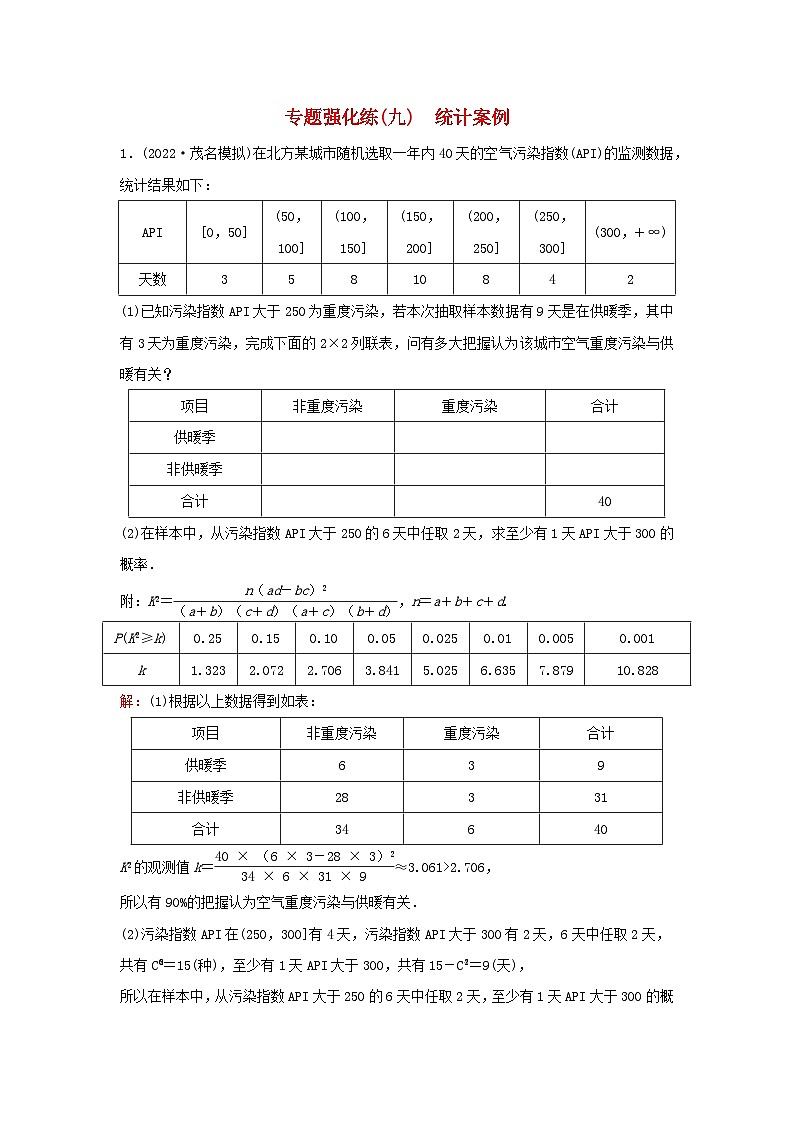
1．(2022·茂名模拟)在北方某城市随机选取一年内40天的空气污染指数(API)的监测数据，统计结果如下：
API
[0，50]
(50，100]
(100，150]
(150，200]
(200，250]
(250，300]
(300，＋∞)
天数
3
5
8
10
8
4
2
(1)已知污染指数API大于250为重度污染，若本次抽取样本数据有9天是在供暖季，其中有3天为重度污染，完成下面的2×2列联表，问有多大把握认为该城市空气重度污染与供暖有关？
项目
非重度污染
重度污染
合计
供暖季



非供暖季



合计


40
(2)在样本中，从污染指数API大于250的6天中任取2天，求至少有1天API大于300的概率．
附：K2＝，n＝a＋b＋c＋d.
P(K2≥k)
0.25
0.15
0.10
0.05
0.025
0.01
0.005
0.001
k
1.323
2.072
2.706
3.841
5.025
6.635
7.879
10.828
解：(1)根据以上数据得到如表：
项目
非重度污染
重度污染
合计
供暖季
6
3
9
非供暖季
28
3
31
合计
34
6
40
K2的观测值k＝≈3.061>2.706，
所以有90%的把握认为空气重度污染与供暖有关．
(2)污染指数API在(250，300]有4天，污染指数API大于300有2天，6天中任取2天，
共有C＝15(种)，至少有1天API大于300，共有15－C＝9(天)，
所以在样本中，从污染指数API大于250的6天中任取2天，至少有1天API大于300的概率为＝.
2．(2022·广东模拟)某科研团队研发针对病毒α的疫苗，并进行接种试验．如果人体在接种疫苗之后的一定时期内产生了针对病毒α的抗体，则称该疫苗有效．该科研团队对其研发的疫苗A和疫苗B，分别进行了接种试验，然后在接种了疫苗A和疫苗B的人群中分别随机抽取了部分个体，并检测其体内是否产生了针对病毒α的抗体，获得样本数据如表：
项目
抽取人数
其中产生抗体人数
接种疫苗A
120
80
接种疫苗B
100
80
(1)从接种疫苗A的人群中任取3人，记产生抗体的人数为X，用样本数据中产生抗体的频率估计概率，求X的分布列及其数学期望；
(2)根据样本数据，是否有95%的把握认为疫苗A与疫苗B的有效性存在差异？说明理由．
附：χ2＝.
P(χ2≥k)
0.050
0.010
0.001
k
3.841
6.635
10.828
解：(1)在接种疫苗A的样本中，产生抗体的频率为＝，
由此估计，从接种疫苗A的人群中任取1人，产生抗体的概率为.
所以从接种疫苗A的人群中任取3人，
产生抗体的人数X～B(3，)，P(X＝k)＝C()k(1－)3－k，其中k＝0，1，2，3，所以X的分布列为
X
0
1
2
3
P




数学期望E(X)＝3×＝2.
(2)有95%的把握认为疫苗A与疫苗B的有效性存在差异．理由如下：
根据样本数据，在接种疫苗A的120人中，80人产生抗体，40人未产生抗体，
在接种疫苗B的100人中，80人产生抗体，20人未产生抗体．
根据公式，χ2＝＝≈4.889>3.841.
所以有95%的把握认为疫苗A与疫苗B的有效性存在差异．
3．(2022·禅城区模拟)某公司研发了一种帮助家长解决孩子早教问题的萌宠机器人．萌宠机器人语音功能让它就像孩子的小伙伴一样和孩子交流，记忆功能还可以记住宝宝的使用习惯，很快找到宝宝想听的内容．同时提供快乐儿歌、国学经典、启蒙英语等早期教育内容，且云端内容可以持续更新．萌宠机器人一投放市场就受到了很多家长欢迎．为了更好地服务广大家长，该公司研究部门从流水线上随机抽取100件萌宠机器人(以下简称产品)，统计其性能指数并绘制频率分布直方图(如图1)


产品的性能指数在[50，70)的适合托班幼儿使用(简称A类产品)，在[70，90)的适合小班和中班幼儿使用(简称B类产品)，在[90，110]的适合大班幼儿使用(简称C类产品)，A，B，C三类产品的销售利润分别为每件1.5，3.5，5.5(单位：元)．以这100件产品的性能指数位于各区间的频率代替产品的性能指数位于该区间的概率．
(1)求每件产品的平均销售利润；
(2)该公司为了解年营销费用x(单位：万元)对年销售量y(单位：万件)的影响，对近5年的年营销费用xi，和年销售量yi(i＝1，2，3，4，5)数据做了初步处理，得到的散点图(如图2)及一些统计量的值．

i
i
(ui－)( vi－)
(ui－)2
16.30
24.87
0.41
1.64
表中ui＝ln xi，vi＝ln yi，＝i，＝i.
根据散点图判断，y＝a·xb可以作为年销售量y(万件)关于年营销费用x(万元)的回归方程．
①建立y关于x的回归方程；
②用所求的回归方程估计该公司应投入多少营销费，才能使得该产品一年的收益达到最大？
(收益＝销售利润－营销费用，取e4.159＝64)．
参考公式：对于一组数据(u1，v1)，(u2，v2)，…，(un，vn)，其回归直线v＝α＋βu的斜率和截距的最小二乘估计分别为＝，＝－.
解：(1)设每件产品的销售利润为ξ元，则ξ的所有可能取值为1.5，3.5，5.5，
由直方图可得，A，B，C三类产品的频率分别为0.15、0.45、0.4，
所以P(ξ＝1.5)＝0.15，
P(ξ＝3.5)＝0.45，
P(ξ＝5.5)＝0.4，
所以随机变量ξ的分布列为：
ξ
1.5
3.5
5.5
P
0.15
0.45
0.4
所以E(ξ)＝1.5×0.15＋3.5×0.45＋5.5×0.4＝4，
故每件产品的平均销售利润为4元．
(2)①由y＝a·xb得，ln y＝ln (a·xb)＝ln a＋bln x，
令u＝ln x，v＝ln y，c＝ln a，则v＝c＋bu，由表中数据可得，＝＝0.25，
则＝－＝－0.25×＝4.159，
所以＝4.159＋0.25u，
即ln ＝4.159＋0.25ln x＝ln(e4.159·x)，
因为e4.159＝64，所以＝64x.
②设年收益为z万元，则z＝E(ξ)·y－x＝256x－x，
设t＝x，f(t)＝256t－t4，
则f′(t)＝256－4t3＝4(64－t3)，
当t∈(0，4)时，f′(t)>0，f(t)在(0，4)单调递增，
当t∈(4，＋∞)时，f′(t)