

2022-2023学年吉林省长春市榆树市八号镇七年级(下)期末数学试卷-普通用卷
展开2022-2023学年吉林省长春市榆树市八号镇七年级(下)期末数学试卷
一、选择题(本大题共8小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
1. 若x2=4,则x的值( )
A. 2 B. ±2 C. 16 D. ±16
2. 在平面直角坐标系中,点P(−1,x2+1)(其中x为任意有理数)一定在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3. 下列数中227,0.101001, 36, 3,无理数是( )
A. 227 B. 0.101001 C. 36 D. 3
4. 不等式−2x+1<3的解集是( )
A. B.
C. D.
5. 我国明代数学读本《算法统宗》一书有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托如果1托为5尺,那么索长和竿子长分别为多少尺?设索长为x尺,竿子长为y尺,可列方程组为( )
A. x−y=52x−y=5 B. x−y=5y−x2=5 C. x−y=5x−y2=5 D. y−x=5x−y2=5
6. 下列图标既不是轴对称图形也不是中心对称图形的是( )
A. B. C. D.
7. 已知,AC//ED,∠C=26°,∠CBE=37°,则∠BED的度数是( )
A. 53°
B. 63°
C. 73°
D. 83°
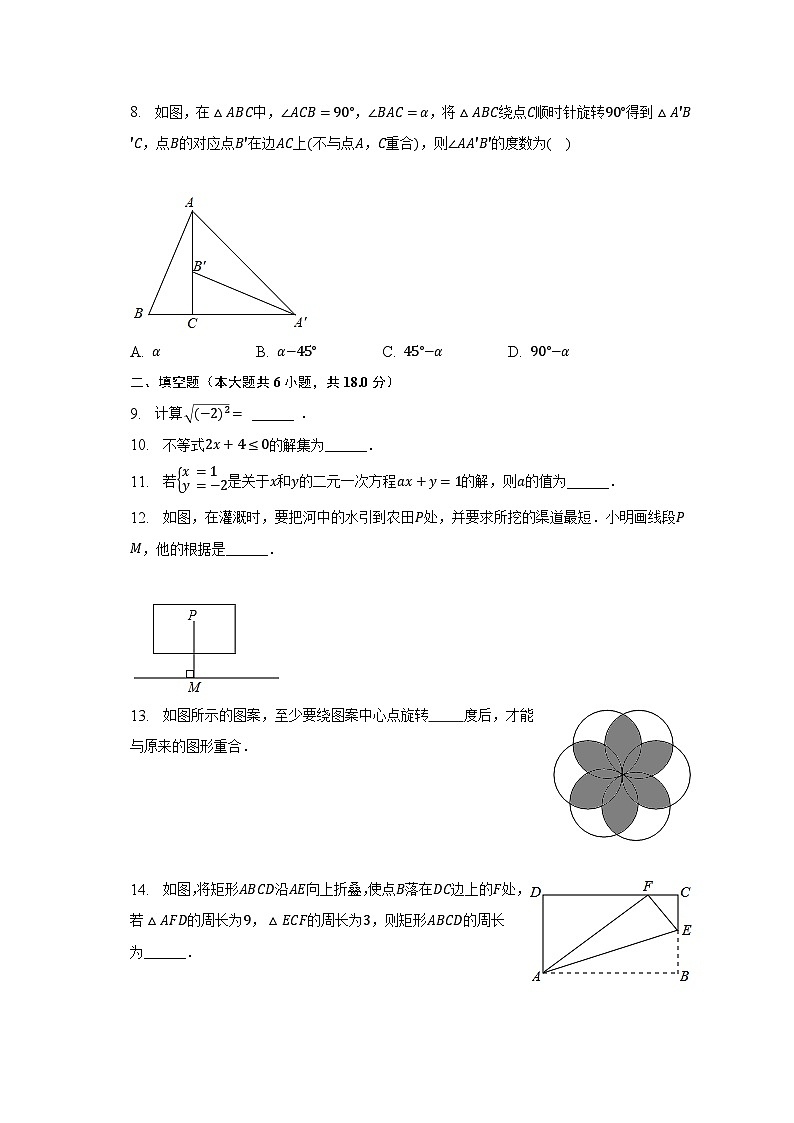
8. 如图,在△ABC中,∠ACB=90°,∠BAC=α,将△ABC绕点C顺时针旋转90°得到△A′B′C,点B的对应点B′在边AC上(不与点A,C重合),则∠AA′B′的度数为( )
A. α B. α−45° C. 45°−α D. 90°−α
二、填空题(本大题共6小题,共18.0分)
9. 计算 (−2)2= ______ .
10. 不等式2x+4≤0的解集为______.
11. 若x=1y=−2是关于x和y的二元一次方程ax+y=1的解,则a的值为______.
12. 如图,在灌溉时,要把河中的水引到农田P处,并要求所挖的渠道最短.小明画线段PM,他的根据是______.
13. 如图所示的图案,至少要绕图案中心点旋转 度后,才能与原来的图形重合.
14. 如图,将矩形ABCD沿AE向上折叠,使点B落在DC边上的F处,若△AFD的周长为9,△ECF的周长为3,则矩形ABCD的周长为______.
三、解答题(本大题共11小题,共88.0分。解答应写出文字说明,证明过程或演算步骤)
15. (本小题8.0分)
计算: 18−38+|1− 2|.
16. (本小题8.0分)
解方程组:x−4y=133x+2y=4.
17. (本小题8.0分)
解不等式:5x+16−2>x−54,并把解集在数轴上表示出来.
18. (本小题8.0分)
被誉为“最美高铁”的长春至珲春城际铁路途经许多隧道和桥梁,其中隧道累计长度与桥梁累计长度之和为342km,隧道累计长度的2倍比桥梁累计长度多36km.求隧道累计长度与桥梁累计长度.
19. (本小题8.0分)
利用平方根的意义求方程(x−1)2=4中x的值.
20. (本小题8.0分)
如图,在△ABC中,∠AED=80°,BD是∠ABC的平分线,DE//BC,求∠EDB的度数.
21. (本小题8.0分)
图①、图②、图③均是8×8的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B、C均为格点.只用无刻度的直尺,分别在给定的网格中按下列要求作图,并保留必要的画图痕迹.
(1)在图①中画出△ABC关于直线l对称的图形.
(2)在图②中画出△ABC关于点O成中心对称的图形.
(3)在图③中,过点C画AB的垂线.
22. (本小题8.0分)
对于下列问题,在解答过程的空白处填上适当的内容(理由或数学式).
如图,在直角△ABC中,CD是斜边AB上的高,∠BCD=35°.
(1)求∠EBC的度数;
(2)求∠A的度数.
解:(1)∵CD⊥AB(已知),
∴∠CDB=______°.
∵∠EBC=∠CDB+∠BCD(______).
∴∠EBC=______°+35°=______°(等量代换).
(2)∵∠EBC=∠A+∠ACB(______),
∴∠A=∠EBC−∠ACB(等式的性质).
∵∠ACB=90°(已知),
∴∠A=______−90°=______°(等量代换).
23. (本小题8.0分)
如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠AFC=______度;
(2)求∠EDF的度数.
24. (本小题8.0分)
我们在数学学习中,经常利用“转化”的思想方法解决问题,比如,我们通过“消元的方法将二元一次方程组转化为一元一次方程,从而求解.下面我们就利用“转化”的思想方法尝试解决新的问题.
先阅读下面的例题,再按要求完成下列问题.
例:解不等式(x−2)(x+1)>0.
解:由有理数的乘法法则“两数相乘,同号得正”,得①x−2>0x+1>0或②x−2<0x+1<0.
解不等式组①,得x>2.
解不等式组②,得x<−1.
所以不等式(x−2)(x+1)>0的解集为x>2或x<−1.
根据例题方法解决下面问题:
(1)解不等式(x+3)(2x−1)<0.
解:由有理数的乘法法则“两数相乘,异号得负”,得①x+3>02x−1<0或②______.
解不等式组①,得______.
解不等式组②,得______.
所以不等式(x+3)(2x−1)<0的解集为______.
(2)应用:不等式:x+2x−1>0的解集为______.
25. (本小题8.0分)
如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(3,c)三点,其中a、b、c满足关系式:|a−2|+(b−3)2+ c−4=0.
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m,12),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在负整数m,使四边形ABOP的面积不小于△AOP面积的两倍?若存在,求出所有满足条件的点P的坐标,若不存在,请说明理由.
答案和解析
1.【答案】B
【解析】解:∵x2=4,
∴x=±2,
即x的值为±2,
故选:B.
如果一个数的平方等于a,这个数就叫做a的平方根,也叫做a的二次方根.依据平方根的定义进行计算即可.
本题主要考查了平方根的定义,要注意一个正数有两个平方根,这两个平方根互为相反数,零的平方根是零,负数没有平方根.
2.【答案】B
【解析】解:∵x2≥0,
∴x2+1≥1,
∴点P(−1,x2+1)在第二象限.
故选:B.
根据平方数非负数判断出纵坐标是正数,然后根据各象限内点的坐标特征解答.
本题考查了点的坐标,根据非负数的性质判断出纵坐标是正数是解题的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(−,+);第三象限(−,−);第四象限(+,−).
3.【答案】D
【解析】解:A.227是分数,属于有理数,故本选项不符合题意;
B.0.101001是有限小数,属于有理数,故本选项不符合题意;
C. 36=6,6是整数,属于有理数,故本选项不符合题意;
D. 3是无理数,故本选项符合题意.
故选:D.
无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
此题考查了无理数的定义.解题的关键是掌握无理数的定义,注意初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…(每两个1之间0的个数依次加1),等有这样规律的数.
4.【答案】A
【解析】解:∵−2x+1<3,
∴−2x<3−1,
−2x<2,
则x>−1,
故选:A.
依次移项、合并同类项、系数化为1即可.
本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.
5.【答案】B
【解析】解:设索长为x尺,竿子长为y尺,
根据题意,可列方程组为x−y=5y−x2=5,
故选:B.
设索长为x尺,竿子长为y尺,根据“索比竿子长一托,对折索子来量竿,却比竿子短一托”,即可得出关于x、y的二元一次方程组,解之即可得出结论.
本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
6.【答案】A
【解析】解:A.既不是轴对称图形也不是中心对称图形,故本选项符合题意;
B.是轴对称图形,不是中心对称图形,故本选项不符合题意;
C.不是轴对称图形,是中心对称图形,故本选项不符合题意;
D.是轴对称图形,不是中心对称图形,故本选项不符合题意;
故选:A.
根据中心对称图形与轴对称图形的概念进行判断即可.
本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与自身重合.
7.【答案】B
【解析】解:∵在△ABC中,∠C=26°,∠CBE=37°,
∴∠CAE=∠C+∠CBE=26°+37°=63°,
∵AC//ED,
∴∠BED=∠CAE=63°.
故选B
因为AC//ED,所以∠BED=∠EAC,而∠EAC是△ABC的外角,所以∠BED=∠EAC=∠CBE+∠C.
本题考查的是两直线平行的性质,关键是根据三角形外角与内角的关系及两直线平行的性质分析.
8.【答案】C
【解析】
【分析】
本题主要考查了旋转的性质、等腰直角三角形的性质,明确旋转前后对应角相等、对应线段相等是解题的关键.
由旋转知AC=A′C,∠BAC=∠CA′B′,∠ACA′=90°,从而得出△ACA′是等腰直角三角形,即可解决问题.
【解答】
解:∵将△ABC绕点C顺时针旋转90°得到△A′B′C,
∴AC=A′C,∠BAC=∠CA′B′,∠ACA′=90°,
∴△ACA′是等腰直角三角形,
∴∠CA′A=45°,
∵∠BAC=α,
∴∠CA′B′=α,
∴∠AA′B′=45°−α.
故选:C.
9.【答案】2
【解析】解: (−2)2= 22=2.
故答案为:2.
直接利用算术平方根化简得出答案.
此题主要考查了算术平方根的化简,正确化简算术平方根是解题关键.
10.【答案】x≤−2
【解析】解:移项,得:2x≤−4,
系数化为1,得:x≤−2,
故答案为:x≤−2.
移项、系数化为1即可得出答案.
本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.
11.【答案】3
【解析】解:将x=1y=−2代入原方程中得a−2=1,
解得:a=3,
∴a的值为3.
故答案为:3.
将x=1y=−2代入原方程,可得出关于a的一元一次方程,解之即可求出a的值.
本题考查了二元一次方程的解,牢记“一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解”是解题的关键.
12.【答案】垂线段最短
【解析】解:要把河中的水引到水池P处,小明画线段PM垂直河岸,使挖的水渠的长度最短,这样做依据的几何学原理是垂线段最短,
故答案为:垂线段最短.
根据垂线段的性质,可得答案.
本题考查了垂线段最短,利用了垂线段的性质:直线外的点与直线上所有点的连线:垂线段最短.
13.【答案】60
【解析】
【分析】
本题考查旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角.
该图形被平分成6部分,因而每部分被分成的圆心角是60°,因而旋转60度的整数倍,就可以与自身重合.
【解答】
解:图案至少要旋转360°6=60°后,才能与原来的图形重合.
故答案为:60.
14.【答案】12
【解析】解:∵△AEF由△AEB折叠而成,
∴△AEF≌△AEB,
∴AF=AB,EF=BE,
∴矩形的周长等于△AFD和△CFE的周长的和为9+3=12.
故答案为:12.
根据图形折叠的性质可知AB=AF,BE=EF,再由△AFD的周长为9,△ECF的周长为3即可得出结论.
本题考查的是翻折变换,熟知折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.
15.【答案】解: 18−38+|1− 2|
=3 2−2+ 2−1
=4 2−3.
【解析】先计算二次根式、开立方和绝对值,后计算加减.
此题考查了实数的混合运算能力,关键是能确定准确的运算顺序,并能对各种运算进行准确计算.
16.【答案】解:x−4y=13①3x+2y=4②,
②×2得:
6x+4y=8③,
①+③得:
7x=21,
解得:x=3,
把x=3代入①得:
3−4y=13,
解得:y=−2.5,
∴原方程组的解为:x=3y=−2.5.
【解析】利用加减消元法,进行计算即可解答.
本题考查了解二元一次方程组,熟练掌握加减消元法是解题的关键.
17.【答案】解:去分母得2(5x+1)−24>3(x−5),
去括号得10x+2−24>3x−15,
移项、合并得7x>7,
系数化为1得x>1,
用数轴表示为:
.
【解析】先去分母,再去括号、移项、合并同类项,然后把x的系数化为1得到不等式的解集,再用数轴表示解集.
本题考查了解简单不等式的能力,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错.
解不等式要依据不等式的基本性质,在不等式的两边同时加上或减去同一个数或整式不等号的方向不变;在不等式的两边同时乘以或除以同一个正数不等号的方向不变;在不等式的两边同时乘以或除以同一个负数不等号的方向改变.
18.【答案】解:设隧道累计长度为x km,桥梁累计长度为y km,
根据题意得:x+y=3422x=y+36,
解得:x=126y=216.
答:隧道累计长度为126km,桥梁累计长度为216km.
【解析】设隧道累计长度为x km,桥梁累计长度为y km,根据“隧道累计长度与桥梁累计长度之和为342km,隧道累计长度的2倍比桥梁累计长度多36km”,即可得出关于x、y的二元一次方程组,解之即可得出结论.
本题考查了二元一次方程组的应用,找准等量关系,列出二元一次方程组是解题的关键.
19.【答案】解:∵(x−1)2=4,由平方根的意义可知:
∴x−1=±2,
∴x−1=2或x−1=−2,
解得:x=3或x=−1.
【解析】直接利用平方根的定义得出答案.
此题主要考查了平方根,正确掌握平方根的定义是解题关键.
20.【答案】解:∵DE//BC且∠AED=80°,
∴∠ABC=∠AED=80°;
∵BD是∠ABC的平分线,
∴∠DBC=12∠ABC,
∴∠DBC=40°,
∵DE//BC,
∴∠EDB=∠DBC=40°.
【解析】首先运用平行线的性质求得∠ABC的度数,再根据角平分线的定义求得∠DBC的度数,然后继续运用平行线的性质求得∠EDB.
本题考查了平行线的性质以及角平分线的概念,比较简单.
21.【答案】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
.
(3)如图,CD即为所求.
【解析】(1)根据轴对称的性质作图即可.
(2)根据中心对称的性质作图即可.
(3)根据点A,B的位置,将点C向左平移4个单位再向上平移1个单位可得到点D,连接CD即可.
本题考查作图−轴对称变换、中心对称,熟练掌握轴对称和中心对称的性质是解答本题的关键.
22.【答案】90 三角形的一个外角等于与它不相邻的两个内角和 90 125 三角形的一个外角等于与它不相邻的两个内角和 125° 35
【解析】解:(1)∵CD⊥AB(已知),
∴∠CDB=90°.
∵∠EBC=∠CDB+∠BCD(三角形的一个外角等于与它不相邻的两个内角和).
∴∠EBC=90°+35°=125°(等量代换).
(2)∵∠EBC=∠A+∠ACB(三角形的一个外角等于与它不相邻的两个内角和),
∴∠A=∠EBC−∠ACB(等式的性质).
∵∠ACB=90°(已知),
∴∠A=125°−90°=35°(等量代换).
故答案为(1)90;三角形的一个外角等于与它不相邻的两个内角和;90;125;
(2)三角形的一个外角等于与它不相邻的两个内角和;125°;35.
(1)由垂直的定义可得∠CDB=90°,利用三角形外角的性质可得可求解∠EBC的度数;
(2)由三角形外角的性质可得∠A=∠EBC−∠ACB,结合∠ACB=90°可求解∠A的度数.
本题主要考查三角形外角的性质,垂直的定义,灵活运用三角形外角的性质是解题的关键.
23.【答案】(1)110
(2)∵∠B=50°,∠BAD=30°,
∴∠ADB=180°−50°−30°=100°,
∵△ABD沿AD折叠得到△AED,
∴∠ADE=∠ADB=100°,
∴∠EDF=∠EDA+∠BDA−∠BDF=100°+100°−180°=20°.
【解析】
解:(1)∵△ABD沿AD折叠得到△AED,
∴∠BAD=∠DAF,
∵∠B=50°,∠BAD=30°,
∴∠AFC=∠B+∠BAD+∠DAF=110°;
故答案为110.
(2)见答案.
【分析】
(1)根据折叠的特点得出∠BAD=∠DAF,再根据三角形一个外角等于它不相邻两个内角之和,即可得出答案;
(2)根据已知求出∠ADB的值,再根据△ABD沿AD折叠得到△AED,得出∠ADE=∠ADB,最后根据∠EDF=∠EDA+∠BDA−∠BDF,即可得出答案.
此题考查了三角形的内角和定理、三角形的外角的性质、翻折变换等问题,解答的关键是沟通外角和内角的关系.
24.【答案】x+3<02x−1>0 −3
【解析】解:(1)解不等式(x+3)(2x−1)<0.
解:由有理数的乘法法则“两数相乘,异号得负”,得①x+3>02x−1<0或②x+3<02x−1>0,
解不等式组①,得−3
所以不等式(x+3)(2x−1)<0的解集为−3
根据由有理数的除法法则“两数相除,同号得正”,得①x+2>0x−1>0或②x+2<0x−1<0,
解不等式组①,得x>1,
解不等式组②,得x<−2,
所以不等式x+2x−1>0的解集为:x>1或x<−2,
故答案为:x>1或x<−2.
(1)仿照例题的方法,进行计算即可解答;
(2)仿照例题的方法,利用有理数的除法法则“两数相除,同号得正”,进行计算即可解答.
本题考查了解一元一次不等式,解一元一次不等式组,熟练掌握例题的方法是解题的关键.
25.【答案】解:(1)∵|a−2|+(b−3)2+ c−4=0,
∴a−2=0,b−3=0,c−4=0,
∴a=2,b=3,b=4;
(2)A点坐标为(0,2),B点坐标为(3,0),
四边形ABOP的面积=S△AOP+S△AOB
=12×2×(−m)+12×2×3
=3−m;
(3)存在.理由如下:
∵S四边形ABOP≥2S△AOP,
∴3−m≥2×12×2×(−m),
∴m≥−3,
∵m为负整数,
∴m=−1或−2或−3,
∴点P的坐标为(−1,12)或(−2,12)或(−3,12).
【解析】本题考查了坐标与图形性质:利用坐标计算线段的长度和判断线段与坐标轴的位置关系.也考查了三角形的面积公式.
(1)根据几个非负数和的性质得到a−2=0,b−3=0,c−4=0,分别解一元一次方程得到a=2,b=3,b=4;
(2)根据三角形的面积公式和四边形ABOP的面积=S△AOP+S△AOB进行计算;
(3)若S四边形ABOP≥2S△AOP,则3−m≥2×12×2×(−m),解得m≥−3,则m=−1,−2,−3,然后分别写出P点的坐标.
2022-2023学年吉林省长春市榆树市八号镇七年级(下)期末数学试卷(含答案解析): 这是一份2022-2023学年吉林省长春市榆树市八号镇七年级(下)期末数学试卷(含答案解析),共14页。试卷主要包含了 若x2=4,则x的值, 下列数中227,0,101001C, 计算 2=______ 等内容,欢迎下载使用。
2022-2023学年吉林省长春市榆树市八号镇七年级(下)期末数学试卷(含解析): 这是一份2022-2023学年吉林省长春市榆树市八号镇七年级(下)期末数学试卷(含解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年吉林省长春市榆树市八号镇八年级(下)期末数学试卷(含解析): 这是一份2022-2023学年吉林省长春市榆树市八号镇八年级(下)期末数学试卷(含解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












