
人教A版 (2019)选择性必修 第一册2.2 直线的方程教学设计
展开2.2.2直线的两点式方程
教学设计
一、教学目标
1.掌握直线的两点式方程的形式、特征及适用范围.
2.掌握直线的截距式方程的形式、特征及适用范围.
3.会选择适当形式求直线方程,并会用直线的两点式方程与截距式方程解答相关问题.
二、教学重难点
1、教学重点
理解并掌握直线的两点式方程与截距式方程.
2、教学难点
直线的两点式方程与截距式方程的应用.
三、教学过程
1、新课导入
在上节课我们学习了直线的点斜式方程和斜截式方程,掌握了在已知直线上一点的坐标和斜率、已知直线斜率和y轴上的截距两种情况下,来求出直线的方程,那么当已知直线上两个点的坐标时,如何求出直线的方程呢?这节课我们就一起来探究一下.
2、探索新知
一、直线的两点式方程
已知直线l经过两点![]() ,
,![]() (其中
(其中![]() ,
,![]() ),当
),当![]() 时,经过两点
时,经过两点![]() ,
,![]() 的直线的斜率
的直线的斜率![]() .任取
.任取![]() ,
,![]() 中的一点,例如,取点
中的一点,例如,取点![]() ,由直线的点斜式方程,得
,由直线的点斜式方程,得![]() ,当
,当![]()
时,上式可写为![]() ,这就是直线的两点式方程,简称两点式.
,这就是直线的两点式方程,简称两点式.
在![]() ,
,![]() 中,如果
中,如果![]() 或
或![]() ,则直线
,则直线![]() 没有两点式方程.当
没有两点式方程.当![]() 时,直线
时,直线![]() 垂直于x轴,直线方程为
垂直于x轴,直线方程为![]() ,即
,即![]() ;当
;当![]() 时,直线
时,直线![]() 垂直于y轴,直线方程为
垂直于y轴,直线方程为![]() ,即
,即![]() .
.
二、直线的截距式方程
例1如图,已知直线l与x轴的交点为![]() ,与y轴的交点为
,与y轴的交点为![]() ,其中
,其中![]() ,
,![]() .求直线l的方程.
.求直线l的方程.
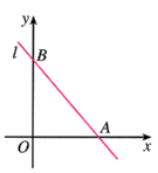
解:将两点![]() ,
,![]() 的坐标代入两点式,得
的坐标代入两点式,得![]() ,即
,即![]() .
.
我们把直线l与x轴的交点![]() 的横坐标a叫做直线在x轴上的截距,此时直线在y轴上的截距是b. 方程
的横坐标a叫做直线在x轴上的截距,此时直线在y轴上的截距是b. 方程![]() 由直线l在两条坐标轴上的截距a与b确定,我们把方程
由直线l在两条坐标轴上的截距a与b确定,我们把方程![]() 叫做直线的截距式方程,简称截距式.
叫做直线的截距式方程,简称截距式.
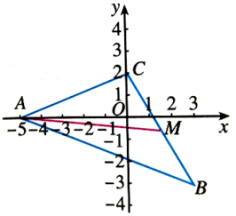
例2 已知![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() ,求边BC所在直线的方程,以及这条边上的中线AM所在直线的方程.
,求边BC所在直线的方程,以及这条边上的中线AM所在直线的方程.
解:如图,过![]() ,
,![]() 的两点式方程为
的两点式方程为![]() ,
,
整理得![]() .
.
这就是边BC所在直线的方程.
边BC上的中线是顶点A与边BC中点M所连线段,
由中点坐标公式,可得点M的坐标为![]() ,即
,即![]() .
.
过![]() ,
,![]() 两点的直线方程为
两点的直线方程为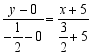 ,
,
整理可得![]() .
.
这就是边BC上中线AM所在直线的方程.
3、课堂练习
1.已知直线![]() 在x轴和y轴上的截距分为a,b,则a,b的值分别为( )
在x轴和y轴上的截距分为a,b,则a,b的值分别为( )
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,7 D.
,7 D.![]() ,
,![]()
2.若直线l过点![]() 和
和![]() ,且点
,且点![]() 在直线l上,则b的值为( )
在直线l上,则b的值为( )
A.2019 B.2018 C.2017 D.2016
3.直线l过点![]() ,且与x轴、y轴分别交于A,B两点,若点P恰为线段
,且与x轴、y轴分别交于A,B两点,若点P恰为线段![]() 的中点,则直线l的方程为_________________.
的中点,则直线l的方程为_________________.
4、小结作业
小结:本节课学习了直线的两点式方程与截距式方程.
作业:完成本节课课后习题.
四、板书设计
2.2.2直线的两点式方程
1.直线的两点式方程:直线l经过两点![]() ,
,![]() (其中
(其中![]() ,
,![]() ),则
),则![]() ,这就是直线的两点式方程,简称两点式.
,这就是直线的两点式方程,简称两点式.
2.直线的截距式方程:方程![]() 叫做直线的截距式方程,简称截距式.其中a叫做直线在x轴上的截距,b是直线在y轴上的截距.
叫做直线的截距式方程,简称截距式.其中a叫做直线在x轴上的截距,b是直线在y轴上的截距.
【小单元教案】高中数学人教A版(2019)选修第一册--2.2.2 直线的两点式方程(课时教学设计): 这是一份【小单元教案】高中数学人教A版(2019)选修第一册--2.2.2 直线的两点式方程(课时教学设计),共7页。教案主要包含了课堂练习1等内容,欢迎下载使用。
高中数学2.2 直线的方程教案: 这是一份高中数学2.2 直线的方程教案,共4页。教案主要包含了教学目标,教学重难点,教学过程,课后作业等内容,欢迎下载使用。
人教A版 (2019)选择性必修 第一册2.2 直线的方程教学设计: 这是一份人教A版 (2019)选择性必修 第一册2.2 直线的方程教学设计,共6页。教案主要包含了教学目标,教学重难点,教学过程,板书设计等内容,欢迎下载使用。













