北师大版八年级上册第三章 位置与坐标3 轴对称与坐标变化教案及反思

这是一份北师大版八年级上册第三章 位置与坐标3 轴对称与坐标变化教案及反思，共5页。教案主要包含了教学目标，教学重点及难点，教学用具，相关资源，教学过程，课堂小结，板书设计等内容，欢迎下载使用。
第三章 位置与坐标3.3轴对称与坐标变化一、教学目标1．经历轴对称变化与点的坐标的变化之间关系的探索过程，发展数形结合意识，初步建立几何直观．2．在直角坐标系中，以坐标轴为对称轴，能写出一个已知顶点坐标的多边形的对称图形的顶点坐标，并知道对应顶点坐标之间的关系．二、教学重点及难点重点：经历图形坐标变化与图形轴对称之间关系的探索过程，明确图形坐标变化与图形轴对称之间关系．难点：由坐标的变化探索新旧图形之间的变化探索过程，发展形象思维能力和数形结合意识．三、教学用具多媒体课件，直尺，三角板．四、相关资源 《复习平面直角坐标系》动画五、教学过程【复习导入】在前几节课中我们学习了平面直角坐标系的有关知识，会画平面直角坐标系；能在方格纸上建立适当的直角坐标系，描述物体的位置；在给定的直角坐标系下，会根据坐标描出点的位置，由点的位置写出它的坐标．我们知道点的位置不同写出的坐标就不同，反过来，不同的坐标确定不同的点．如果坐标中的横（纵）坐标不变，纵（横）坐标按一定的规律变化，或者横纵坐标都按一定的规律变化，那么图形是否会变化，变化的规律是怎样的，这将是本节课中我们要研究的问题．【探究新知】探索两个关于坐标轴对称的图形的坐标关系1．在如图所示的平面直角坐标系中，第一、二象限内各有一面小旗．两面小旗之间有怎样的位置关系？对应点A与A1的坐标又有什么特点？其它对应的点也有这个特点吗？2．在右边的坐标系内，任取一点，做出这个点关于y轴对称的点，看看两个点的坐标有什么样的位置关系，说说其中的道理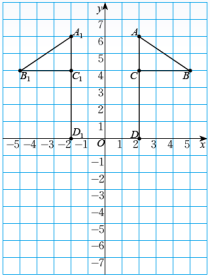．答：（1）关于y轴对称．对应点A与A1的横坐标互为相反数，纵坐标相同，其它对应的点也有这个特点．（2）做出的两个点的横坐标互为相反数，纵坐标相同．【典例精讲】例1　在平面直角坐标系中依次连接下列各点：（0，0），（5，4），（3，0），（5，1），（5，－1），（3，0），（4，－2），（0，0）你得到了一个怎样的图案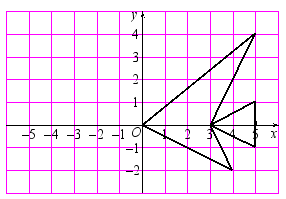？做以下变化：（1）纵坐标保持不变，横坐标分别乘以－1，再将所得的点用线段依次连接起来，所得的图案与原来的图案相比有什么变化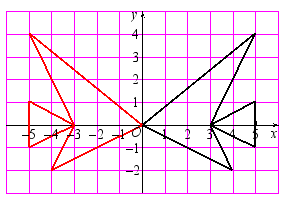？（2）横坐标保持不变，纵坐标分别乘以－1，再将所得的点用线段依次连接起来，所得的图案与原来的图案相比有什么变化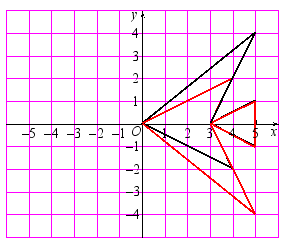？解析：先根据题意写出变化后的坐标，然后根据变化后的坐标，把变化后的图形在自己准备的方格纸上画出来．你们画出的图形与下面的图形相同吗？这个图形与原来的图形相比有什么变化呢？（1）所得的图案与原图案关于纵轴成轴对称．（2）所得的图案与原图案关于横轴成轴对称． 议一议关于x轴对称的两个点的坐标之间有什么关系？关于y轴呢？ 学生思考，讨论，归纳得出结论：关于x轴对称的两个点的坐标，横坐标相同，纵坐标互为相反数．关于y轴对称的两个点的坐标，纵坐标相同，横坐标互为相反数．【课堂练习】1．将平面直角坐标系内某个图形各个点的横坐标不变，纵坐标都乘以－1，所得图形与原图形的关系是（   ）A．关于x轴对称    B．关于y轴对称   C．关于原点对称    D．无法确定2．在平面直角坐标系中，将点A（1，2）的横坐标乘以－1，纵坐标不变，得到点A’，则点A与点A’的关系是(    ) A．关于x轴对称     B．关于y轴对称C．关于原点对称     D．将点A向x轴负方向平移一个单位得A3．点（4，3）与点（4，－3）的关系是（  ） ．A．关于原点对称    B．关于x轴对称C．关于y轴对称    D．不能构成对称关系
4．在平面直角坐标系中，点A（2，3）与点B关于x轴对称，则点B的坐标为（   ）A．(3，2)     B．(－2，－3)    C．(－2，3)    D．(2，－3)5．点M(1，2)关于y轴对称的点坐标为(      ) A．(－1，2)   B．(1，－2)     C．(2，－1)     D．(－1，－2)．6．点（m，－1）和点（2，n）关于 x轴对称，则 mn等于(    )    A．－2     B．2     C．1      D．－17．已知A、B两点的坐标分别是(－2，3)和(2，3），则下面四个结论：①A、B关于x轴对称；②A、B关于y轴对称；③A、B关于原点对称；④A、B之间的距离为4，其中正确的有(     )A．1个     B．2个    C．3个     D．4个8．若P（a，3－b），Q(5，2)关于x轴对称，则a=     ， b=     ．9．点A（2，－3）关于x 轴对称的点的坐标是        ．10．点B（－2，1）关于 y 轴对称的点的坐标是         ．答案： 1．A；2．B；3．B；4．D；5．A；6．B；7．B；8．5，5；9．(2，3)；10．(2，1)．六、课堂小结对称：1．纵坐标不变，横坐标分别乘－1，所得图形与原图形关于y轴对称；2．横坐标不变，纵坐标分别乘－1，所得图形与原图形关于x轴对称；七、板书设计3.3  轴对称与坐标变化1．纵坐标不变，横坐标分别乘－1，所得图形与原图形关于y轴对称2．横坐标不变，纵坐标分别乘－1，所得图形与原图形关于x轴对称