2023八年级数学下册第17章勾股定理小结课第2课时课件（人教版）

这是一份2023八年级数学下册第17章勾股定理小结课第2课时课件（人教版），共30页。

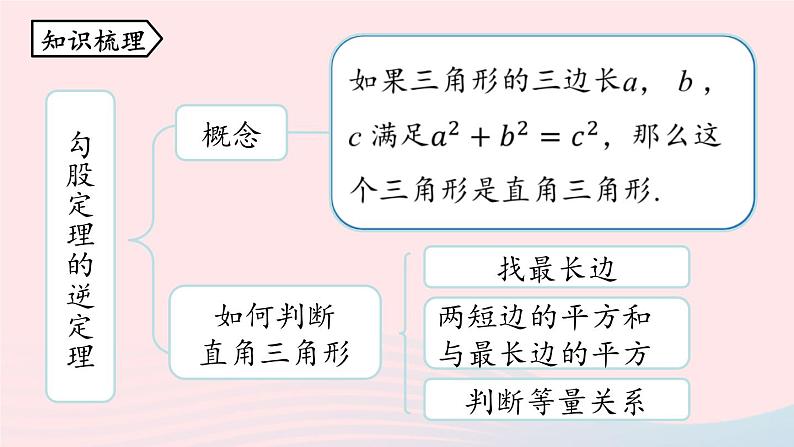
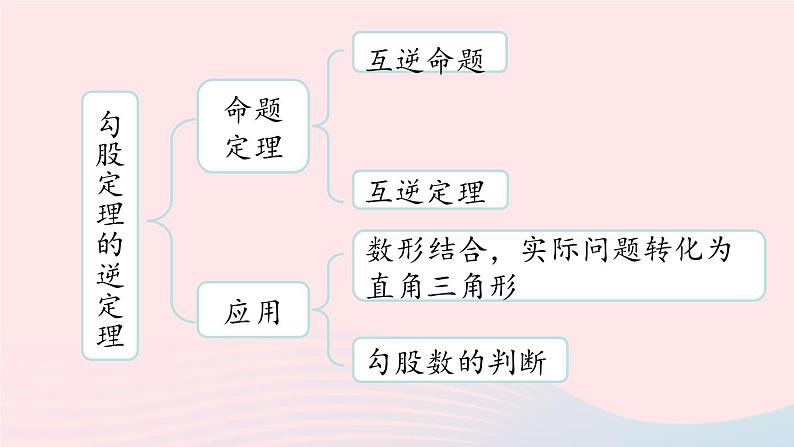
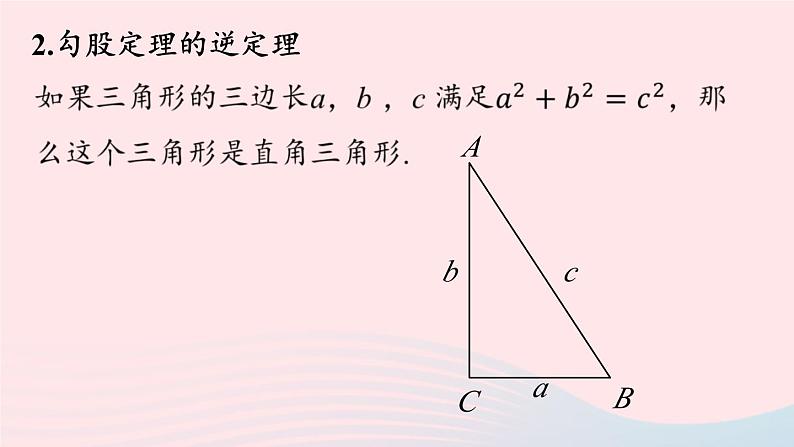
17 勾股定理 小结八年级下册 RJ初中数学课时2勾股定理的逆定理概念 如何判断直角三角形找最长边判断等量关系两短边的平方和与最长边的平方知识梳理勾股定理的逆定理命题定理互逆命题互逆定理应用数形结合，实际问题转化为直角三角形勾股数的判断互逆命题：如果两个命题的题设、结论正好相反，那么这两个命题叫做 .如果把其中一个叫做 ，那么另外一个叫做它的 .1.互逆命题和互逆定理互逆命题原命题逆命题互逆定理：一般地，如果一个定理的逆命题经过证明是正确的，那么它也是一个定理，称这两个定理 ，其中一个定理叫做另外一个定理的 .互为逆定理逆定理2.勾股定理的逆定理 3. 勾股定理逆定理的应用② 实质：由“数”到“形”的转化；③ 应用：判定一个三角形是否为直角三角形. 4. 勾股数 正整数勾股数判断一组数是不是勾股数的步骤：看、找、算、判.1.写出下列命题的逆命题，并判断这些命题的真假.（1）如果∠A和∠B是邻补角，那么∠A+∠B=180〫.解：（1）逆命题：如果∠A+∠B=180〫，那么∠A和∠B是邻补角. 它的逆命题为假命题.重难点1：互逆命题和互逆定理重点解析（2）逆命题：如果一个三角形两个内角所对的边相等，那么这两个内角相等. （2）如果一个三角形的两个内角相等，那么这两个内角所对的边相等.它的逆命题为真命题.2.下列各命题中，逆命题成立的是（ ）.A.全等三角形的对应角相等.B.如果两个实数相等，那么它们的绝对值相等.C.两直线平行，同位角相等.D.如果两个角都是30〫，那么这两个角相等.CA.逆命题：对应角相等的两个三角形全等.（ ）B.逆命题：如果两个实数的绝对值相等，那么它们相等.（ ）C.逆命题：同位角相等，两直线平行.（ ）D.逆命题：如果两个角相等，那么这两个角都是30〫.（ ）假假假真两个大小不一样的等腰直角三角形-2和2的绝对值相等两个角都是40〫注意：1.有些命题在不容易确定题设和结论的情况下，可以先改写成“如果……那么……”的形式，然后确定题设和结论. 2.判断一个命题是假命题只需要举出一个反例即可.（1）在△ABC中，∠A=25〫,∠B=65〫；判断满足下列条件的三角形是不是直角三角形.如果是，请指出哪个角是直角.解：（1）在△ABC中，因为∠A=25〫,∠B=65〫，所以∠C=180〫-∠A-∠B=90〫，所以这个三角形是直角三角形.∠C是直角.重难点2：勾股定理的逆定理重点解析（2）在△ABC中，AB=15， BC=20 ，AC=25；  所以这个三角形是直角三角形，∠B是直角.（3）在△ABC中，AB=14， BC=2 ，AC=15.  所以这个三角形不是直角三角形.判定三角形为直角三角形的方法1.用角判定：如果已知条件与角有关，只要说明三角形有一个内角为90〫 即可.2.用边判定：如果已知条件与边有关，则可以通过勾股定理的逆定理进行判定.   重难点3：勾股定理逆定理的应用重点解析  判断下列各组数是不是勾股数：    重难点4：勾股数重点解析1.在△ABC中，∠A, ∠B , ∠C的对边分别是a , b , c,下列判断错误的是（ ）.BA.如果∠C- ∠B= ∠A，则△ABC是直角三角形.   深化练习A.如果∠C- ∠B= ∠A，则△ABC是直角三角形.解析：因为∠C- ∠B=∠A，所以 ∠C=∠B+∠A.因为∠C+∠B+∠A=180〫，所以 ∠C+∠C=180〫.解得∠C=90〫，所以△ABC是直角三角形.  可以看出b是斜边，所以∠B=90〫，选项B错误.    因为∠C+∠B+∠A=180〫，所以 10x=180〫，解得x=18〫.所以∠A=90〫，所以△ABC是直角三角形.2.在Rt△ABC中， ∠C=90〫，若AB=10，则两个正方形的面积之和为 .解析：由图可知，AC 是小正方形的边长，BC 是大正方形的边长.100  即两个正方形的面积之和为100.    4.如图，南北向 MN 为我国领海线，即 MN 以西为我国领海，以东为公海，上午 9 时 50 分，我国反走私艇 A 发现正东方有一走私艇 C以 13 海里/时的速度偷偷向我领海开来，便立即通知正在MN线上巡逻的我国走私艇 B 密切注意.反走私艇 A 和走私艇 C 的距离为 13 海里,A,B 两艇的距离是 5 海里;反走私艇 B 离走私艇 C 12 海里,若走私艇 C 的速度不变,最早会在什么时候进入我国领海？解：设 MN 与 AC 交于点 E，则∠BEC=90〫. 所以△ABC为直角三角形，且∠ABC=90〫.