2024全国一轮数学（基础版）第10讲 指数与指数函数课件PPT

这是一份2024全国一轮数学（基础版）第10讲 指数与指数函数课件PPT，共36页。PPT课件主要包含了链教材·夯基固本，激活思维，基础回归，研题型·融会贯通，举题说法，随堂内化，5＋∞等内容，欢迎下载使用。

1. (人A必一P109习题2(1))设a>0，则下列运算中正确的是(　　)
A. 是偶函数且在R上是增函数B. 是奇函数且在R上是增函数C. 是偶函数且在R上是减函数D. 是奇函数且在R上是减函数
3. 下列函数的值域是(0，＋∞)的有(　　)
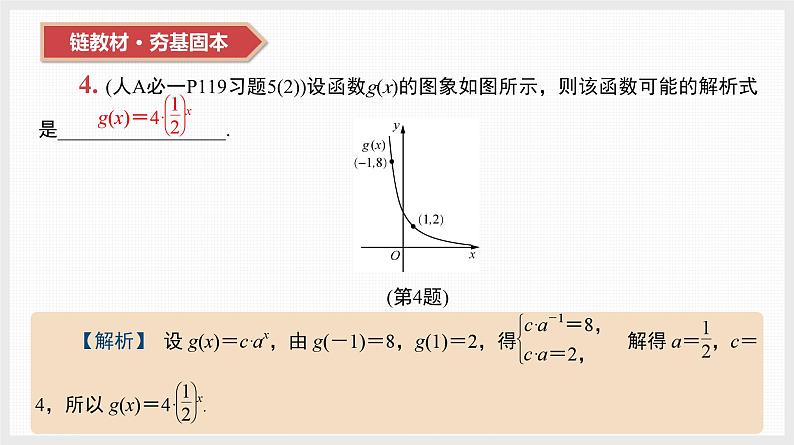
4. (人A必一P119习题5(2))设函数g(x)的图象如图所示，则该函数可能的解析式是_________________.(第4题)
5. 函数y＝ax＋2 024＋2 023(a>0，a≠1)的图象恒过定点_____________________.
(－2 024,2 024)
(2) 有理指数幂的运算性质：aras＝_______；(ar)s＝_______；(ab)r＝_______，其中a>0，b>0，r，s∈Q.
3. 指数函数及其性质(1) 概念：函数y＝ax(a>0且a≠1)叫做指数函数，其中指数x是自变量，函数的定义域是R，a是底数．(2) 指数函数的图象与性质
例1　指数式的求值与化简．
指数幂运算的一般原则：(1) 有括号的先算括号里的，无括号的先做指数运算．(2) 先乘除后加减，负指数幂化成正指数幂的倒数．(3) 底数是负数，先确定符号，底数是小数，先化成分数，底数是带分数的，先化成假分数．(4) 若是根式，应化为分数指数幂，尽可能用幂的形式表示，运用指数幂的运算性质来解答．(5) 运算结果形式力求统一．
因此函数f(x)在(－∞，0)上单调递减，在(0，＋∞)上单调递增．
例2　已知函数f(x)＝|2x－1|.(1) 求函数f(x)的单调区间；
【解答】 在同一平面直角坐标系中分别作出函数f(x)，f(x＋1)的图象如图所示．
(2) 比较f(x＋1)与f(x)的大小．
【解析】 如图，观察易知a，b的关系为a1. (多选)已知实数a，b满足等式2 023a＝2 024b，则下列关系式可能成立的是(　 　)A. 0所以当x>1时，y＝2x－1是增函数，当x≤1时，y＝21－x是减函数，且当x＝1时，y＝1，即函数的图象过点(1,1)，所以符合条件的图象是A.
2. 函数y＝2|1－x|的图象大致是(　　)A B C D
【解析】 作出曲线|y|＝2x＋1与直线y＝b，如图所示，(第3题)由图象可得，要想曲线|y|＝2x＋1与直线y＝b没有公共点，则b应满足的条件是b∈[－1,1]．
3. 若曲线|y|＝2x＋1与直线y＝b没有公共点，则b的取值范围是_____________.
A. b【解析】 对于A，因为f(x＋2kπ)＝2sin(x＋2kπ)＝2sin x＝f(x)(k∈Z)，所以f(x)是周期函数，故A正确．
(2) (2022·淄博一模)(多选)已知函数f(x)＝2sin x，下列结论正确的是(　　)A. f(x)是周期函数B. f(x)的图象关于原点对称
所以f(x)在(－∞，－2)上单调递减，在(－2，＋∞)上单调递增，故函数f(x)的增区间是(－2，＋∞)，减区间是(－∞，－2)．
(1) 若a＝－1，求f(x)的单调区间；
解得a＝1，故当f(x)有最大值3时，实数a的值为1.
(2) 若f(x)有最大值3，求a的值；
因此只能a＝0，故当f(x)的值域为(0，＋∞)时，a的值为0.
(3) 若f(x)的值域是(0，＋∞)，求a的值．
点击对应数字即可跳转到对应题目
A. 1 B. 2 C. －1 D. ±1
当a＝－1时，f(x)的定义域为R，符合题意，当a＝1时，f(x)的定义域为(－∞，0)∪(0，＋∞)，符合题意．
3. 已知函数f(x)＝ax－b的图象如图所示，其中a，b为常数，则下列结论正确的是(　　)(第3题)A. a>1，b<0B. a>1，b>0C. 00D. 0【解析】 由f(x)＝ax－b的图象可以观察出函数f(x)＝ax－b在定义域上单调递减，所以0又其图象无限接近直线y＝1但又不与该直线相交，所以b＝1，从而a＝－1，所以a－b＝－2.