九年级上册1 菱形的性质与判定授课ppt课件

这是一份九年级上册1 菱形的性质与判定授课ppt课件，共32页。PPT课件主要包含了合作学习，一组邻边相等，菱形的定义，菱形的性质研究，性质定理2，菱形的性质，菱形的四条边相等，菱形的邻角互补，学以致用，答案4cm等内容，欢迎下载使用。

菱形具有工整,匀称,美观等许多优点,常被人们用在图案设计上.
1.1.1菱形的性质
欣赏下面图片，图片中框出的图形是你熟悉的吗？
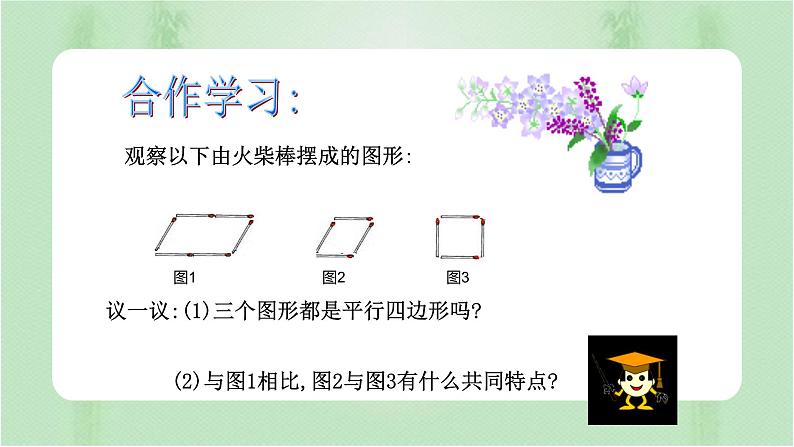
观察以下由火柴棒摆成的图形:
议一议:(1)三个图形都是平行四边形吗?
(2)与图1相比,图2与图3有什么共同特点?
有一组邻边相等的平行四边形叫做菱形
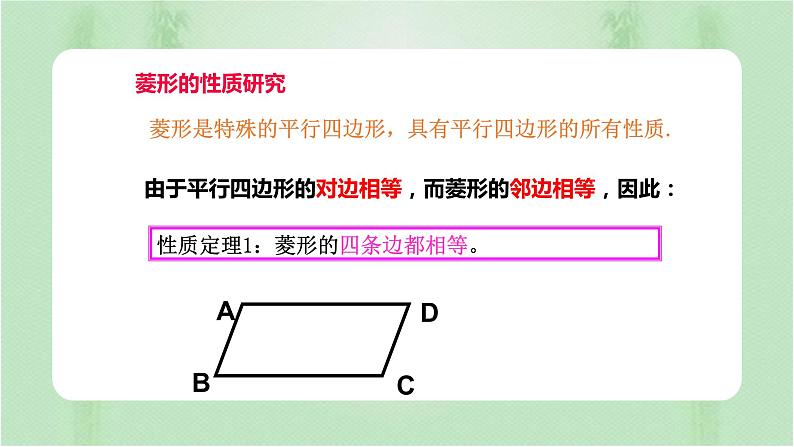
由于平行四边形的对边相等，而菱形的邻边相等，因此：
性质定理1：菱形的四条边都相等。
菱形是特殊的平行四边形，具有平行四边形的所有性质.
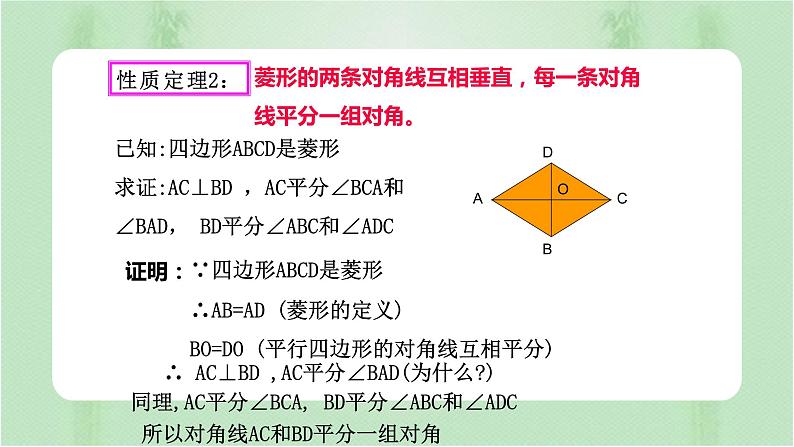
菱形的两条对角线互相垂直，每一条对角线平分一组对角。
∵四边形ABCD是菱形
已知:四边形ABCD是菱形求证:AC⊥BD ，AC平分∠BCA和∠BAD， BD平分∠ABC和∠ADC
∴AB=AD (菱形的定义)BO=DO (平行四边形的对角线互相平分)
∴ AC⊥BD ,AC平分∠BAD(为什么?)
同理,AC平分∠BCA, BD平分∠ABC和∠ADC
所以对角线AC和BD平分一组对角
菱形的两条对角线互相平分
菱形的两组对边平行且相等
菱形的两组对角分别相等
菱形的两条对角线互相垂直，每一 条对角线平分一组对角
想一想 平行四边形、菱形是不是轴对称图形？如果是轴对称图形，对称轴分别有几条
平行四边形不是轴对称图形，但是中心对称图形。
菱形是轴对称图形，对称轴有两条，也是中心对称图形。
2.菱形的两条对角线的长分别为6 cm和8 cm，则菱形的边长是 （ ）
A.10 cm B.7 cmC.5 cm D.4 cm
1.已知菱形的周长是12cm，那么它的边长是______.
3.如图，P是菱形ABCD的对角线AC上一点，PE⊥AD于点E，PE=4 cm，求点P到AB的距离.
【例1】 如图，在菱形ABCD中，CE⊥AB于点E，CF⊥AD于点F，求证：AE＝AF.
证明：连结AC. ∵四边形ABCD是菱形， ∴AC平分∠BAD， 即∠BAC＝∠DAC. ∵CE⊥AB，CF⊥AD， ∴∠AEC＝∠AFC＝90°. 又∵AC＝AC，∴△ACE≌△ACF. ∴AE＝AF.
【例2】如图，已知菱形ABCD的边长为2cm，∠BAD＝120°，对角线AC、BD相交于点O.试求这个菱形的两条对角线AC与BD的长.
解：在菱形ABCD中，∵∠ABC+∠BAD＝180°，　∠BAD＝120°，∴ ∠ABC＝60°.又∵AB＝BC，∴ △ABC是等边三角形.∴AC＝AB＝2，
在Rt△ABO中，AB＝２，AO＝1,
思考:计算菱形的面积除了上式方法外,利用对角线能计算菱形的面积公式吗?
面积：S菱形=底×高=对角线乘积的一半
【例3】如图，菱形ABCD的两条对角线AC，BD的长度分别为4 cm，3 cm，求菱形ABCD的面积和周长．
1.如图，已知菱形的两条对角线的长分别为6cm和8cm，则这个菱形的高DE为（　　） C.5cm
2.如图,四边形ABCD是边长为13cm的菱形,其中对 角线BD长10cm.
求:(1)对角线AC的长度; (2)菱形ABCD的面积.
∵四边形ABCD是菱形,
(2)菱形ABCD的面积
∴AC=2AE=2×12=24(cm).
请利用两个全等的等腰（不等边）三角形纸片拼成一个平行四边形。
有几种拼法？其中有菱形？你是如何判定的?
1.1.2菱形的判定
∵在四边形ABCD中,AB=BC=CD=DA，∴四边形ABCD是菱形.
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?
对角线互相垂直的平行四边形是菱形.
∴ ABCD是菱形
又∵ AC ⊥ BD,
∵四边形ABCD是平行四边形，
(有一组邻边相等的平行四边形叫做菱形).
(线段垂直平分线上的点到线段两个端点的距离相等)
∵四边形ABCD是平行四边形,AC ⊥ BD,
∴ □ ABCD是菱形.
【例4】如图，在□ABCD中，对角线AC，BD相交于点O，过点O作MN⊥BD，分别交AD，BC于点M，N.求证：四边形BNDM是菱形.
证明：∵四边形ABCD是平行四边形，∴AD∥BC，OD=OB.∴∠MDO=∠NBO.∵MN⊥BD，∴∠MOD=∠NOB=90°.∴△MOD≌△NOB（ASA）.∴MD=NB.又∵ MD∥NB，∴四边形BNDM是平行四边形.又∵MN⊥BD，∴四边形BNDM是菱形.
取一张长方形纸片,按下图的方法对折两次,并沿图(3)中的斜线剪开,把剪下的1这部分展开,平铺在桌面上.
(1)剪出的这个图形是哪一种四边形?这是什么四边形?
(2) 根据折叠, 剪裁的过程,你能说明你的判断的理由吗?
如图,将矩形纸片ABCD沿着某条直线折叠,使点A与点C重合,剪除没有重叠的部分,再铺开.
1、剪得的四边形是什么四边形?你能说明理由吗?
2、若AB=6㎝,BC=8㎝ , 则折痕的长度是多少?
把两张等宽的纸条交叉重叠在一起，你能判断重叠部分ABCD的形状吗？
1.菱形具有而一般平行四边形不具有的性质是（ ） A.对角相等 B.对边相等 C.对角线互相垂直 D.对角线相等
2.如图，在菱形ABCD中，AC=8，BD=6，则 △ABD的周长等于 （　　） A.18 B.16 C.15 D.14
3.根据下图填一填：（1）已知菱形ABCD的周长是12cm，那么它的边长 是 ______.（2）在菱形ABCD中，∠ABC＝120 °，则∠BAC＝ _______.（3）菱形ABCD的两条对角线长分别为6cm和8cm， 则菱形的边长是_______.
(4)菱形的一个内角为120°,平分这个内角的对角 线长为11cm，则菱形的周长为______.
(5)菱形的面积为64平方厘米，两条对角线的长度比 为1∶2 ,那么菱形最短的那条对角线长为_______.
4.如图,四边形ABCD是边长为13cm的菱形,其中对 角线BD长10cm.