
- 浙江省杭州市2023年各地区中考数学模拟(一模)试题按题型难易度分层分类汇编(9套)-03解答题(基础题) 试卷 1 次下载
- 浙江省杭州市2023年各地区中考数学模拟(一模)试题按题型难易度分层分类汇编(9套)-03解答题(提升题)1 试卷 0 次下载
- 浙江省台州市2023年各地区中考数学模拟(一模)试题按题型难易度分层分类汇编(6套)-01选择题 试卷 0 次下载
- 浙江省台州市2023年各地区中考数学模拟(一模)试题按题型难易度分层分类汇编(6套)-02填空题 试卷 0 次下载
- 浙江省台州市2023年各地区中考数学模拟(一模)试题按题型难易度分层分类汇编(6套)-03解答题(提升题) 试卷 0 次下载
浙江省杭州市2023年各地区中考数学模拟(一模)试题按题型难易度分层分类汇编(9套)-03解答题(提升题)2
展开浙江省杭州市2023年各地区中考数学模拟(一模)试题按题型难易度分层分类汇编(9套)-03解答题(提升题)2
一.反比例函数与一次函数的交点问题(共2小题)
1.(2023•滨江区一模)直线y1=k1x+b(k1,b为常数,且k1≠0)与双曲线(k为常数,且k2≠0)相交于A(2,﹣4),B(4,n)两点,O为坐标原点.
(1)求上述一次函数与反比例函数的表达式.
(2)当y1>y2时,请直接写出x的取值范围.
(3)求△OAB的面积.
2.(2023•萧山区一模)已知函数和函数y2=k2x+b(k1,k2,b是常数,k1k2≠0).
(1)若两函数的图象交于点A(1,4),点B(a,1),求函数y1,y2的表达式.
(2)若点C(﹣1,n)向上平移6个单位恰好落在函数y1上,又点C(﹣1,n)向右平移2个单位恰好落在函数y2上,且k1+k2=0,求b的值.
二.抛物线与x轴的交点(共2小题)
3.(2023•西湖区一模)已知二次函数y=x2﹣(a+2)x+2a+1,
(1)若a=4,求函数的对称轴和顶点坐标.
(2)若函数图象向下平移一个单位,恰好与x轴只有一个交点,求a的值.
(3)若抛物线过点(﹣1,y0),且对于抛物线上任意一点(x1,y1)都有y1≥y0,若点A(m,n),B(2﹣m,p)是这条抛物线上不同的两点,求证:n+p>﹣8.
4.(2023•滨江区一模)二次函数y=ax2+bx+c(a≠0)与x轴交于A(1,0),B(m,0)两点.
(1)当a=1,b=2时,求m的值.
(2)当0<a<2,c=2时,
①求证:m>1.
②点C(x1,y1),D(x2,y2)在该抛物线上,且x1>x2,x1+x2<2,试比较y1与y2的大小.
三.二次函数综合题(共1小题)
5.(2023•萧山区一模)已知二次函数y=ax2+2x+1(a≠0).
(1)若,试求该二次函数图象与x轴的交点坐标.
(2)若该二次函数图象的顶点坐标为(s,t),求证:t=s+1.
(3)若a<0,且当自变量x满足0≤x≤m时,﹣2≤y≤2,求m的值.
四.四边形综合题(共3小题)
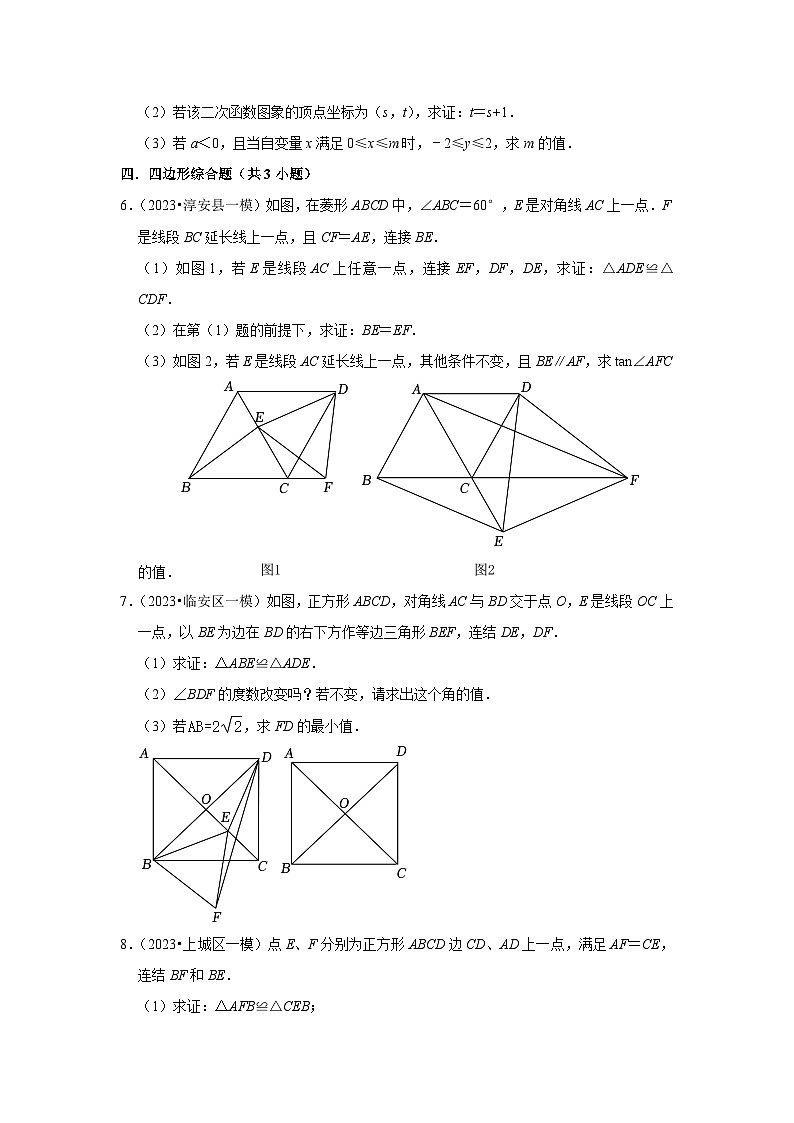
6.(2023•淳安县一模)如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上一点.F是线段BC延长线上一点,且CF=AE,连接BE.
(1)如图1,若E是线段AC上任意一点,连接EF,DF,DE,求证:△ADE≌△CDF.
(2)在第(1)题的前提下,求证:BE=EF.
(3)如图2,若E是线段AC延长线上一点,其他条件不变,且BE∥AF,求tan∠AFC的值.
7.(2023•临安区一模)如图,正方形ABCD,对角线AC与BD交于点O,E是线段OC上一点,以BE为边在BD的右下方作等边三角形BEF,连结DE,DF.
(1)求证:△ABE≌△ADE.
(2)∠BDF的度数改变吗?若不变,请求出这个角的值.
(3)若,求FD的最小值.
8.(2023•上城区一模)点E、F分别为正方形ABCD边CD、AD上一点,满足AF=CE,连结BF和BE.
(1)求证:△AFB≌△CEB;
(2)过点E作EM⊥BF交AB于点M,垂足为点N.
①判断△MBE的形状,并说明理由;
②当M在AB边上时,设∠ABF=α,△BMN和△BFA的面积分别是S1和S2,求证:.
五.圆周角定理(共1小题)
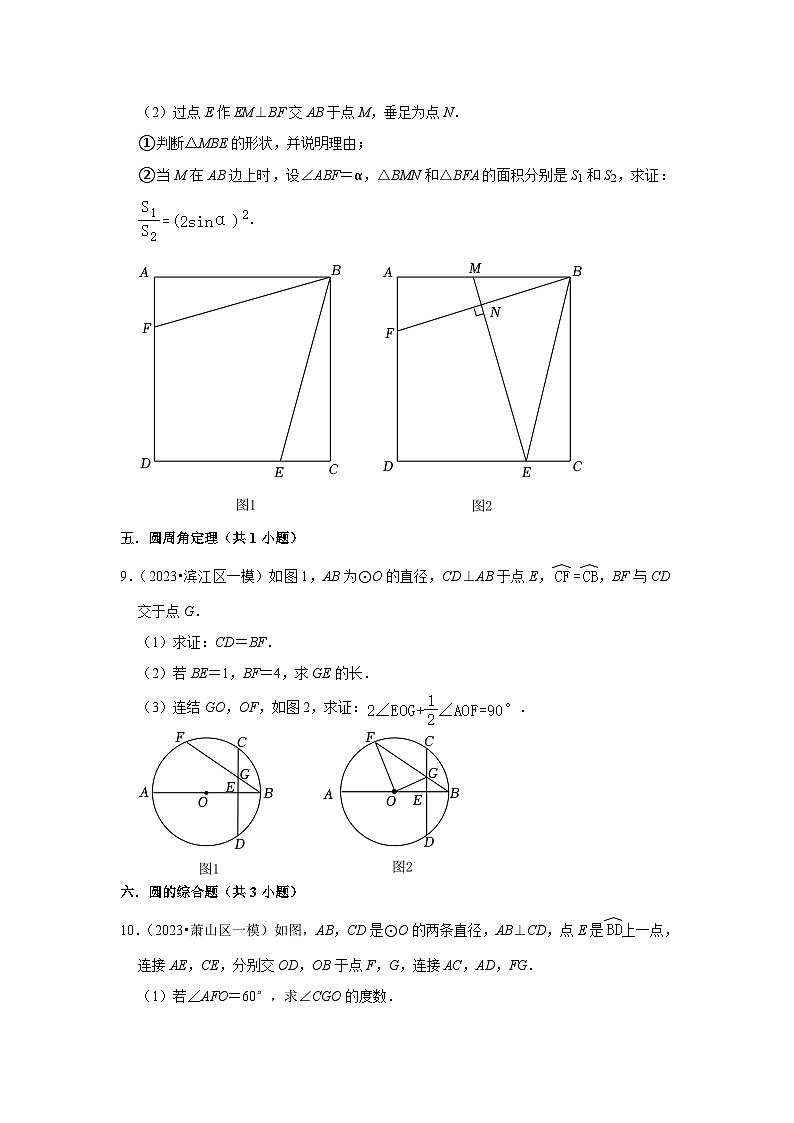
9.(2023•滨江区一模)如图1,AB为⊙O的直径,CD⊥AB于点E,,BF与CD交于点G.
(1)求证:CD=BF.
(2)若BE=1,BF=4,求GE的长.
(3)连结GO,OF,如图2,求证:.
六.圆的综合题(共3小题)
10.(2023•萧山区一模)如图,AB,CD是⊙O的两条直径,AB⊥CD,点E是上一点,连接AE,CE,分别交OD,OB于点F,G,连接AC,AD,FG.
(1)若∠AFO=60°,求∠CGO的度数.
(2)求证:AC2=AG•CF.
(3)设∠AFO=α,△CFG的面积为S1,△AOF的面积为S2,求证:=tanα﹣1.
11.(2023•杭州一模)如图,点A,B,C分别是⊙O上的三等分点,连接AB,BC,CA.点D,E分别是AC,BC上的点,且BE=CD.过点D作EO的垂线,垂足为H,与⊙O分别交于N、M,与边AB交于F点.
(1)求证:△ABC是等边三角形;
(2)探索FN与MD的数量关系,并加以证明;
(3)点E从点B沿BC方向运动到点C,点H也随之运动,若⊙O的半径为2,则点H运动的路径长是多少?
12.(2023•桐庐县一模)如图1,AB是⊙O的直径,BC是⊙O的切线,点D是直径AB右侧半圆上一点,过点D作DE⊥AB于点E,连结AC交DE于点P.
(1)求证:AC•PE=AP•BC.
(2)连结OC、AD,若AD∥OC,求证:PE=PD.
(3)如图2,连结CD,若CD是⊙O的切线,求证:PE=PD.
七.相似三角形的判定与性质(共1小题)
13.(2023•萧山区一模)如图,正方形ABCD中,点M是对角线BD上一点,连结AM并延长交BC于点E,连结CM.
(1)求证:AM=CM.
(2)若∠CME=45°,求的值.
八.相似形综合题(共2小题)
14.(2023•桐庐县一模)如图1,在平行四边形ABCD中,∠ABC的平分线与AD边相交于点E,若∠D=60°.
(1)求:.
(2)如图2,连结CE并延长,与BA延长线相交于点F,求证:AF•DE=CD2.
(3)在(2)条件下,连结DF,若AB=4,求△DEF的面积.
15.(2023•西湖区一模)已知E是正方形ABCD边CD上任意一点,
(1)将△ADE沿AE翻折至△AEF,
①如图1,若F点恰好在对角线AC上,,求AB的长.
②如图2,若点E是CD中点,若S△ADE=2,射线AF与BC边交于点G,求四边形EFGC的面积.
(2)如图3,点Q是边BC上任意一点,记DQ与AE的交于点H,射线AE与射线BC交于点P,求证:BP•HE=AH•QC.
浙江省杭州市2023年各地区中考数学模拟(一模)试题按题型难易度分层分类汇编(9套)-03解答题(提升题)2
参考答案与试题解析
一.反比例函数与一次函数的交点问题(共2小题)
1.(2023•滨江区一模)直线y1=k1x+b(k1,b为常数,且k1≠0)与双曲线(k为常数,且k2≠0)相交于A(2,﹣4),B(4,n)两点,O为坐标原点.
(1)求上述一次函数与反比例函数的表达式.
(2)当y1>y2时,请直接写出x的取值范围.
(3)求△OAB的面积.
【答案】(1)y1=x﹣6,;
(2)0<x<2或;
(3)6.
【解答】解:(1)把A(2,﹣4)代入y2=得,﹣4=,
解得k2=﹣8,
∴y2=﹣,
把点B(4,n)代入y2=﹣得到,n=﹣=﹣2,
∴B(4,﹣2),
把A(2,﹣4),B(4,﹣2)代入y1=k1x+b得,,
解得,
∴y1=x﹣6,
(2)由图象可知,当y1>y2时,x的取值范围是0<x<2或x>4;
(3)S△OAB=×4×2=6,
即△OAB的面积是6.
2.(2023•萧山区一模)已知函数和函数y2=k2x+b(k1,k2,b是常数,k1k2≠0).
(1)若两函数的图象交于点A(1,4),点B(a,1),求函数y1,y2的表达式.
(2)若点C(﹣1,n)向上平移6个单位恰好落在函数y1上,又点C(﹣1,n)向右平移2个单位恰好落在函数y2上,且k1+k2=0,求b的值.
【答案】(1)y1=,y2=﹣x+5;
(2)b=﹣6.
【解答】解:(1)∵点A(1,4),点B(a,1)在函数图象上,
∴k1=1×4=a×1,
∴k1=4,a=4,
∴函数y1的表达式为y1=,B(4,1),
把点A(1,4),点B(4,1)代入y2=k2x+b,得,
解得,
∴函数y2的表达式为y2=﹣x+5;
(2)∵点C(﹣1,n)向上平移6个单位恰好落在函数y1上,
∴点(﹣1,n+6)在函数上,
∴k1=﹣1×(n+6)=﹣n﹣6,
∵点C(﹣1,n)向右平移2个单位恰好落在函数y2上,
∴点(1,n)在函数y2=k2x+b上,
∴n=k2+b,
∴k2=n﹣b,
∵k1+k2=0,
∴﹣n﹣6+(n﹣b)=0,
∴b=﹣6.
二.抛物线与x轴的交点(共2小题)
3.(2023•西湖区一模)已知二次函数y=x2﹣(a+2)x+2a+1,
(1)若a=4,求函数的对称轴和顶点坐标.
(2)若函数图象向下平移一个单位,恰好与x轴只有一个交点,求a的值.
(3)若抛物线过点(﹣1,y0),且对于抛物线上任意一点(x1,y1)都有y1≥y0,若点A(m,n),B(2﹣m,p)是这条抛物线上不同的两点,求证:n+p>﹣8.
【答案】(1)x=3,(3,0);
(2)a=2;
(3)见详解.
【解答】解:(1)∵a=4,
∴y=x2﹣(4+2)x+8+1,
∴y=x2﹣6x+9,
∴y=(x﹣3)2,
∴函数的对称轴和顶点坐标分别为:直线x=3,(3,0);
(2)函数图象向下平移一个单位得y=x2﹣(a+2)x+2a+1﹣1,
∴y=x2﹣(a+2)x+2a与x轴只有一个交点,
∴Δ=(a+2)2﹣4×2a=0,
解方程得:a=2;
(3)∵抛物线过点(﹣1,y0),且对于抛物线上任意一点(x1,y1)都有y1≥y0,
∴(﹣1,y0)为抛物线的顶点,
∴抛物线的对称轴为x=﹣1,
∴,
∴a=﹣4,
∴抛物线为:y=x2+2x﹣7,
∵A(m,n),B(2﹣m,p)在抛物线上,
∴n=m2+2m﹣7,p=(2﹣m)2+2(2﹣m)﹣7,
∴n+p=m2+2m﹣7+(m﹣2)2+2(2﹣m)﹣7,
∴n+p=2(m﹣1)2﹣8,
∵A(m,n),B(2﹣m,p)是这条抛物线上不同的两点,
∴m≠2﹣m,
∴m≠1
∴n+p>﹣8.
4.(2023•滨江区一模)二次函数y=ax2+bx+c(a≠0)与x轴交于A(1,0),B(m,0)两点.
(1)当a=1,b=2时,求m的值.
(2)当0<a<2,c=2时,
①求证:m>1.
②点C(x1,y1),D(x2,y2)在该抛物线上,且x1>x2,x1+x2<2,试比较y1与y2的大小.
【答案】(1)﹣3;
(2)①见解析;②y1<y2.
【解答】解:(1)当a=1,b=2时,y=x2+2x+c,
把A(1,0)代入得,0=1+2+c,
解得c=﹣3,
∴y=x2+2x﹣3,
把B(m,0)代入y=x2+2x﹣3得,0=m2+2m﹣3,
解得m=1或﹣3;
∵二次函数y=ax2+bx+c(a≠0)与x轴交于A(1,0),B(m,0)两点,
∴m=﹣3;
(2)①把A(1,0),B(m,0)代入y=ax2+bx+c(a≠0)得,
a+b+c=0,am2+bm+c=0,
∵c=2,
∴a+b+2=0,am2+bm+2=0,
由b=﹣a﹣2得到am2﹣(a+2)m+2=0,
则Δ=(a+2)2﹣4a×2=(a﹣2)2≥0,
∴,
∴m1=1(舍去),,
∵0<a<2,
∴m>1.
②由①得b=﹣a﹣2,c=2,
∴y=ax2﹣(a+2)x+2,
把C(x1,y1),D(x2,y2)代入得y1,y2,
∵x1>x2,x1+x2<2,
∴x1<2﹣x2,
∵0<a<2,
∴2a﹣(a+2)=a﹣2<0,
∴a(x1+x2)<0,
∴y1﹣y2=(x1﹣x2),
∴y1<y2.
三.二次函数综合题(共1小题)
5.(2023•萧山区一模)已知二次函数y=ax2+2x+1(a≠0).
(1)若,试求该二次函数图象与x轴的交点坐标.
(2)若该二次函数图象的顶点坐标为(s,t),求证:t=s+1.
(3)若a<0,且当自变量x满足0≤x≤m时,﹣2≤y≤2,求m的值.
【答案】(1)该二次函数图象与x轴的交点坐标为(﹣2+,0),(﹣2﹣,0);
(2)证明见解答过程;
(3)m的值为3.
【解答】(1)解:当a=时,y=x2+2x+1,
令y=0得0=x2+2x+1,
解得x=﹣2+或x=﹣2﹣,
∴该二次函数图象与x轴的交点坐标为(﹣2+,0),(﹣2﹣,0);
(2)证明:∵二次函数y=ax2+2x+1图象的顶点坐标为(s,t),
∴s=﹣=﹣,t==1﹣,
∴t=1+s;
(3)解:在y=ax2+2x+1中,令x=0得y=1,
由(2)知抛物线y=ax2+2x+1顶点坐标为(﹣,1﹣),
∵a<0,当0≤x≤m时,﹣2≤y≤2,
∴当x=m时函数值最小为﹣2,当x=﹣时,函数值(1﹣)最大为2,
∴,
解得或(不符合题意,舍去),
∴m的值为3.
四.四边形综合题(共3小题)
6.(2023•淳安县一模)如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上一点.F是线段BC延长线上一点,且CF=AE,连接BE.
(1)如图1,若E是线段AC上任意一点,连接EF,DF,DE,求证:△ADE≌△CDF.
(2)在第(1)题的前提下,求证:BE=EF.
(3)如图2,若E是线段AC延长线上一点,其他条件不变,且BE∥AF,求tan∠AFC的值.
【答案】(1)证明见解答;
(2)证明见解答;
(3)tan∠AFC的值是﹣2.
【解答】(1)证明:∵四边形ABCD是菱形,∠ABC=60°,
∴AB∥CD,∠ADC=∠ABC=60°,AD=CD,
∴∠DCF=∠ABC=60°,△ACD是等边三角形,
∴∠DAE=60°,
∴∠DAE=∠DCF,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS).
(2)证明:∵AB=CB,∠ABC=60°,
∴△ABC是等边三角形,
∴∠BAE=60°,
∴∠BAE=∠DAE,
∵AB=AD,AE=AE,
∴△BAE≌△DAE(SAS),
∴BE=DE,
∵△ADE≌△CDF,
∴DE=DF,∠ADE=∠CDF,
∴∠EDF=∠CDE+∠CDF=∠CDE+∠ADE=∠ADC=60°,
∴△DEF是等边三角形,
∴EF=DE,
∴BE=EF.
(3)解:如图2,点E是线段AC延长线上一点,
∵AD=CD,∠DAE=∠DCF,AE=CF,
∴△ADE≌△CDF(SAS),
∴AE=CF,
∵BE∥CF,
∴△ECB∽△ACF,
∴=,
∴CF•EC=AC•CB,
作AH⊥BF于点H,设AC=CB=a,AE=CF=x,则EC=x﹣a,
∴x(x﹣a)=a2,
解关于x的方程得x1=a,x2=a(不符合题意,舍去),
∴CF=a,
∵∠AHF=90°,∠ACB=60°,
∴AH=AC•sin60°=a,CH=AC•cos60°=a,
∴FH=CF+CH=a+a=a,
∴tan∠AFC===﹣2,
∴tan∠AFC的值是﹣2.
7.(2023•临安区一模)如图,正方形ABCD,对角线AC与BD交于点O,E是线段OC上一点,以BE为边在BD的右下方作等边三角形BEF,连结DE,DF.
(1)求证:△ABE≌△ADE.
(2)∠BDF的度数改变吗?若不变,请求出这个角的值.
(3)若,求FD的最小值.
【答案】(1)证明见解析部分;
(2)30°;
(3)2.
【解答】(1)证明:∵四边形ABCD是正方形,
∴∠EAD=∠EAB=45°,
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS);
(2)解:∵△ABE≌△ADE,
∴EB=ED,
∵△BEF是等边三角形,
∴EB=EF,∠BEF=60°,
∴EB=EF=ED,
∴点E是△BDF是外心,
∴∠BDF=∠BEF=30°;
(3)解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD=2,∠BCD=90°,
∴BD=BC=4,
∵∠BDF=30°,点E在线段OC上运动,
∴观察图象可知当点E与O重合时,AF的长最小,此时BF⊥DF,
∴DF=BD•cos30°=4×=2.
∴DF的最小值为2.
8.(2023•上城区一模)点E、F分别为正方形ABCD边CD、AD上一点,满足AF=CE,连结BF和BE.
(1)求证:△AFB≌△CEB;
(2)过点E作EM⊥BF交AB于点M,垂足为点N.
①判断△MBE的形状,并说明理由;
②当M在AB边上时,设∠ABF=α,△BMN和△BFA的面积分别是S1和S2,求证:.
【答案】(1)证明过程见解答;
(2)①△MBE是等腰三角形,理由见解答;
②证明过程见解答.
【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=CB,∠A=∠C=90°,
在△AFB和△CEB中,
,
∴△AFB≌△CEB(SAS);
(2)①解:△MBE是等腰三角形,理由如下:
∵△AFB≌△CEB,
∴∠AFB=∠CEB,
∵EM⊥BF,
∴∠BNM=∠A=90°,
∴∠BMN=∠AFB,
∴∠BMN=∠CEB,
∵AB∥CD,
∴∠EBM=∠CEB,
∴∠BMN=∠EBM,
∴EB=EM,
∴△MBE是等腰三角形;
②证明:∵△AFB≌△CEB,
∴∠ABF=∠CBE=α,
∵∠BNM=∠A=90°,∠MBN=∠FBA,
∴△BMN∽△BFA,
∵△BMN和△BFA的面积分别是S1和S2,
∴=()2,
如图,过点E作EG⊥AB于点G,
∵EB=EM,
∴∠BEG=∠MEG,BG=MG=BM,
∵∠EGB=∠CBG=∠C=90°,
∴四边形EGBC是矩形,
∴EG∥BC,
∴∠BEG=∠CBE=α,
∴sin∠BEG=sinα==,
∴=2sinα,
∴.
五.圆周角定理(共1小题)
9.(2023•滨江区一模)如图1,AB为⊙O的直径,CD⊥AB于点E,,BF与CD交于点G.
(1)求证:CD=BF.
(2)若BE=1,BF=4,求GE的长.
(3)连结GO,OF,如图2,求证:.
【答案】(1)见解析;
(2)GE的长为;
(3)见解析.
【解答】(1)证明:∵AB为⊙O的直径,CD⊥AB于点E,
∴,
∵,
∴,
∴,即,
∴BF=CD;
(2)解:如图所示:连接BC,
由(1)得:,CD=BF=4,
∴∠FBC=∠BCD,
∴BG=CG,
∵AB为⊙O的直径,CD⊥AB于点E,
∴,
设EG=x,则BG=CG=2﹣x,
在△BEG中,EG2+BE2=BG2,即x2+12=(2﹣x)2,
解得:,
∴GE的长为;
(3)解:如图所示:连接OC交BF于I,
∵,
∴,
在△OCG和△OBG中,
,
∴△OCG≌△OBG(SSS),
∴∠COG=∠BOG,
∴∠IOB=2∠EOG,
∵OF=OB,OC为半径,
∴OC⊥BF,
∴∠OIB=90°,
∵∠IOB+∠IBO=90°,
∴.
六.圆的综合题(共3小题)
10.(2023•萧山区一模)如图,AB,CD是⊙O的两条直径,AB⊥CD,点E是上一点,连接AE,CE,分别交OD,OB于点F,G,连接AC,AD,FG.
(1)若∠AFO=60°,求∠CGO的度数.
(2)求证:AC2=AG•CF.
(3)设∠AFO=α,△CFG的面积为S1,△AOF的面积为S2,求证:=tanα﹣1.
【答案】(1)75°;
(2)证明见解析;
(3)证明见解析.
【解答】(1)解:∵AB,CD是⊙O的两条直径,AB⊥CD,
∴=90°,
∴∠D=∠E=∠ACD=∠BAC=45°,
又∵∠AFO=∠D+∠DAE=60°,
∴∠DAE=15°,
∴∠DCE=∠DAE=15°,
∴∠AGC=90°﹣∠DCE=75°;
(2)证明:∵∠ACG=∠ACD+∠CDE=45°+∠CDE,∠AFC=∠D+∠DAE=45°+∠DAE,
∴∠ACG=∠AFC,
又∵∠ACF=∠CAG=45°,
∴△ACF∽△GAC,
∴,
∴AC2=AG•CF.
(3)证明:∵S△ACD=,S四边形ACGF=AG•CF,
由(2)知AC2=AG•CF,
∴S△ACD=S四边形ACGF,
∴S△ACD﹣S△ACO=S四边形ACGF﹣S△ACO,
∴S△AFD=S△CGF,
∴==﹣1=﹣1=tanα﹣1.
11.(2023•杭州一模)如图,点A,B,C分别是⊙O上的三等分点,连接AB,BC,CA.点D,E分别是AC,BC上的点,且BE=CD.过点D作EO的垂线,垂足为H,与⊙O分别交于N、M,与边AB交于F点.
(1)求证:△ABC是等边三角形;
(2)探索FN与MD的数量关系,并加以证明;
(3)点E从点B沿BC方向运动到点C,点H也随之运动,若⊙O的半径为2,则点H运动的路径长是多少?
【答案】(1)证明见解答;
(2)FN=MD,证明见解答;
(3)点H运动的路径长是.
【解答】(1)证明:∵点A,B,C分别是⊙O上的三等分点,
∴==,
∴AB=BC=AC,
∴△ABC是等边三角形.
(2)解:FN=MD,
证明:如图1,连接OC、OD、OE、EF,
∵△ABC是⊙O的内接正三角形,
∴∠BOC=×360°=120°,∠A=∠ABC=∠ACB=60°,
∵OB=OC,
∴∠OBC=∠OCB=30°,
∴∠OBE=∠OCD=30°,
∵BE=CD,
∴△OBE≌△OCD(SAS),
∴OE=OD,∠BOE=∠COD,
∴∠EOD=∠COE+∠COD=∠COE+∠BOE=∠BOC=120°,
∴∠OED=∠ODE=30°,
∵DH⊥EO交EO的延长线于点H,
∴∠DHE=90°,
∴∠EDF=60°,
∵∠CDE=180°﹣∠EDF﹣∠ADF=120°﹣∠ADF,∠AFD=180°﹣∠A﹣∠ADF=120°﹣∠ADF,
∴∠CDE=∠AFD,
∵BC=AC,BE=CD,
∴CE=AD,
∴△CDE≌△AFD(AAS),
∵DE=FD,
∴△DEF是等边三角形,
∵EH⊥DF,
∴FH=DH,NH=MH,
∴FN=MD.
(3)解:如图2,延长BO交AC于点K,连接并延长KH交AB于点L,
∵∠OBC=∠OBA=30°,
∴BK平分∠ABC,
∴BK⊥AC,AK=CK,
∴∠OKD=∠OHD=90°,
取OD的中点I,连接IK、IH,则IK=IH=IO=ID=OD,
∴K、H、O、D四点都在以OD为直径的圆上,
∴∠OKH=∠ODH=30°,
∴∠OKH=∠OBC,
∴KH∥BC,
∴点H在过点K与BC平行的直线上运动,
∴线段KL就是点E从点B运动到点C时点H的运动路径,
∵∠OKC=90°,∠OCK=30°,OC=2,
∴OK=OC=1,
∴AK=CK===,
∵∠A=60°,∠AKL=∠ACB=60°,
∴∠ALK=60°,
∴△ALK是等边三角形,
∵KL=AK=,
∴点H运动的路径长是.
12.(2023•桐庐县一模)如图1,AB是⊙O的直径,BC是⊙O的切线,点D是直径AB右侧半圆上一点,过点D作DE⊥AB于点E,连结AC交DE于点P.
(1)求证:AC•PE=AP•BC.
(2)连结OC、AD,若AD∥OC,求证:PE=PD.
(3)如图2,连结CD,若CD是⊙O的切线,求证:PE=PD.
【答案】(1)证明见解答;
(2)证明见解答;
(3)证明见解答.
【解答】证明:(1)∵AB是⊙O的直径,BC是⊙O的切线,
∴BC⊥AB,
∵DE⊥AB于点E,AC交DE于点P,
∴PE∥BC,
∴△AEP∽△ABC,
∴=,
∴AC•PE=AP•BC.
(2)如图1,延长AD、BC交于点F,
∵AD∥OC,
∴==1,
∵PE∥CB,
∴△APE∽△ACB,
∴=,
∵PD∥CF,
∴△APD∽△ACF,
∴=,
∴=,
∴==1,
∴PE=PD.
(3)如图2,连结AD并延长AD、BC交于点G,连结BD、OD、OC,
∵CB、CD都是⊙O的切线,
∴CB=CD,∠OCB=∠OCD,
∴OC⊥BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AG⊥BD,
∴AG∥OC,
∴==1,
∵PE∥CB,
∴△APE∽△ACB,
∴=,
∵PD∥CG,
∴=,
∴=,
∴==1,
∴PE=PD.
七.相似三角形的判定与性质(共1小题)
13.(2023•萧山区一模)如图,正方形ABCD中,点M是对角线BD上一点,连结AM并延长交BC于点E,连结CM.
(1)求证:AM=CM.
(2)若∠CME=45°,求的值.
【答案】(1)证明见解析;(2)1.
【解答】(1)证明:∵四边形ABCD为正方形,
∴AD=CD,∠ADM=∠CDM=45°,
在△ADM和△CDM中,
,
∴△ADM≌△CDM(SAS),
∴AM=CM;
(2)解:∵△ADM≌△CDM,
∴∠AMD=∠CMD,
∵∠CME=45°,
∴∠AMC=135°.
∴∠AMD=∠CMD=∠AMC=67.5°,
∵∠ADM=∠CDM=45°,
∴∠DAM=∠DCM=67.5°,
∴∠DMC=∠DCM=67.5°,
∴DC=DM.
设正方形的边长为a,则AB=CD=DM=a,BD=AB=a,
∴BM=BD﹣DM=(1)a.
∵四边形ABCD为正方形,
∴∠ABM=45°,
∴∠ABM=∠CME=45°.
∵∠AMD=∠CMD,∠BAD=∠BCD=90°,
∴∠BAM=∠BCM,
∴△ABM∽△CME,
∴.
∴=﹣1.
八.相似形综合题(共2小题)
14.(2023•桐庐县一模)如图1,在平行四边形ABCD中,∠ABC的平分线与AD边相交于点E,若∠D=60°.
(1)求:.
(2)如图2,连结CE并延长,与BA延长线相交于点F,求证:AF•DE=CD2.
(3)在(2)条件下,连结DF,若AB=4,求△DEF的面积.
【答案】(1);
(2)证明见解析部分;
(3)4.
【解答】(1)解:如图1中,过点A作AH⊥BE于点H.
∵四边形ABCD是平行四边形,
∴AD∥BC,∠D=∠ABC=60°,
∵BE平分∠ABC
∴∠ABE=∠EBC=∠AEB=30°,
∴AB=AE,
∵AH⊥BE,
∴BH=EH,
∵cos∠ABH==,
∴=;
(2)证明:∵四边形ABCD是平行四边形,
∴BF∥CD,AB=CD,
∵AB=AE,
∴AE=CD,
∵AF∥CD,
∴△AFE∽△DCE,
∴=,
∴CD2=AF•DE;
(3)解:连接DF,过点F作FH⊥AE于点H.
∵AD∥BC,
∴∠FAH=∠ABC=60°,
∴FH=AF•cos60°=AF,
∵CD=4,
∴AF•DE=CD2=16,
∵S△DEF=•DE•FH=•AF•DE=4.
15.(2023•西湖区一模)已知E是正方形ABCD边CD上任意一点,
(1)将△ADE沿AE翻折至△AEF,
①如图1,若F点恰好在对角线AC上,,求AB的长.
②如图2,若点E是CD中点,若S△ADE=2,射线AF与BC边交于点G,求四边形EFGC的面积.
(2)如图3,点Q是边BC上任意一点,记DQ与AE的交于点H,射线AE与射线BC交于点P,求证:BP•HE=AH•QC.
【答案】(1)①;
②1;
(2)证明见解答过程.
【解答】(1)解:①∵四边形ABCD是正方形,
∴∠D=90°,∠ACD=45°,AB=CD,
设AB=x=CD,
∵,
∴,
∵将△ADE沿AE翻折至△AEF,
∴△ADE≌△AEF,
∴,
∴,即,
解得,
即;
②分别延长AE,BC,交于点M,
∵四边形ABCD是正方形,
∴∠D=∠B=90°,AD∥BC,AB=CD=AD=BC,
∴∠M=∠DAE,∠D=∠ECM,
∵点E是CD中点,
∴,
∴,△ADE≌△MCE(AAS),
解得:,
∴,
∵将△ADE沿AE翻折至△AEF,
∴△ADE≌△AEF,
∴∠DAE=∠FAE,
∴∠M=∠FAE,
∴AG=MG,
设CG=t,则,,
在Rt△ABG中,由勾股定理得:AB2+BG2=AG2,
即,
解得:,
∴,
∴四边形EFGC的面积=;
(2)证明:设AD=x,CQ=m,CP=y,则BP=x+y,
∴,
∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DAH=∠QPH,∠ADH=∠PQH,
∴△ADH∽△PQH,
∴,
∴xPH=(m+y)AH,
又∵∠AED=∠PEC,
∴△ADE∽△PCE,
∴,
∴,
∴yAH+yHE=xPH﹣xHE,
即yAH+(x+y)HE=xPH,
∴yAH+(x+y)HE=(m+y)AH,
∴(x+y)HE=mAH,
∴,
∴,
即BP•HE=AH•QC.
山东省淄博市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-03解答题(提升题): 这是一份山东省淄博市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-03解答题(提升题),共26页。试卷主要包含了÷÷,其中x为不等式组的整数解,,如图所示,两点,且对称轴为直线x=4等内容,欢迎下载使用。
山东省泰安市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-03解答题(提升题): 这是一份山东省泰安市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-03解答题(提升题),共27页。试卷主要包含了先化简,再求值,,一次函数的图象与x轴交于点C,两点,交y轴于点C,问题等内容,欢迎下载使用。
山东省威海市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-03解答题(提升题): 这是一份山东省威海市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-03解答题(提升题),共22页。试卷主要包含了数据网络引领时代发展,在该函数图象上等内容,欢迎下载使用。












