吉林省辽源市田家炳高级中学2019-2020学年高一下学期期中考试数学试题 Word版含解析

www.ks5u.com田家炳高中2019-2020第二学期期中考试数学试题

注意事项：1.试卷满分：150分.答题时间：120分钟.

2.本试卷总页数2页；共22小题，考试结束时请将答题卡与答题纸一并交回.

第Ⅰ卷（选择题  共60分）

一.选择题：本大题共12个小题，每小题5分，共60分，在每四个小题的选项中只有一个是符合题目要求的.

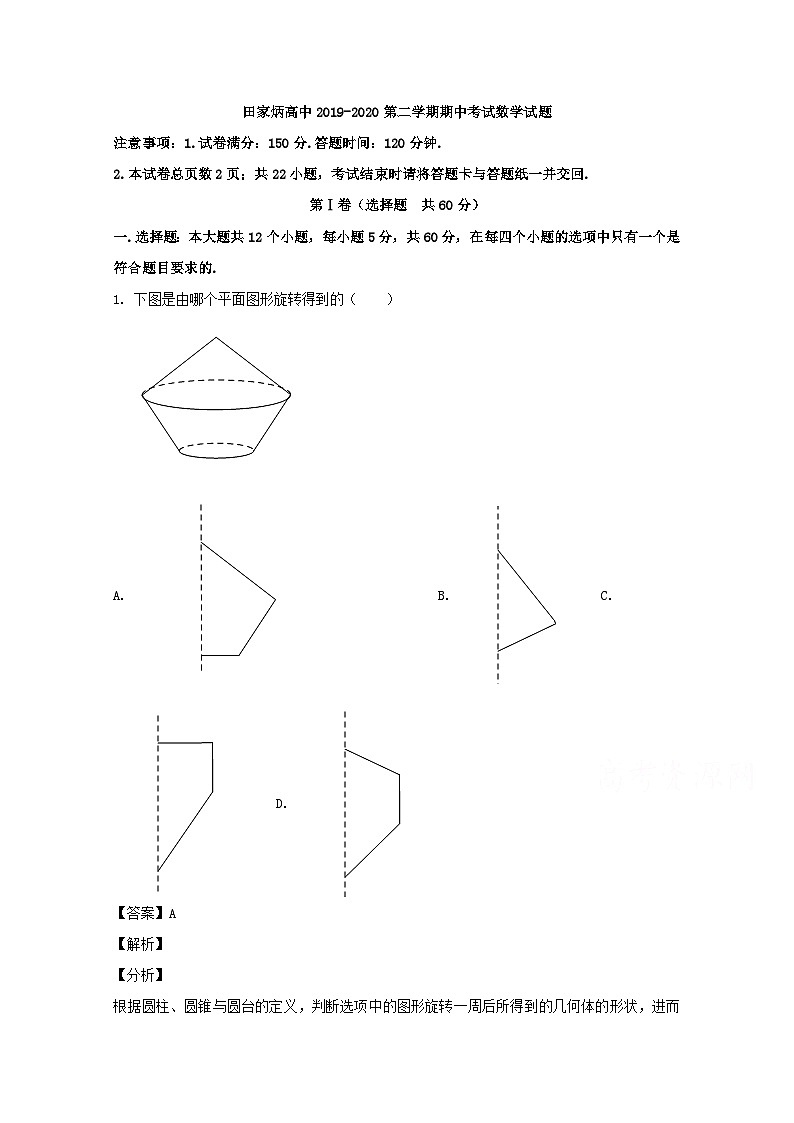
1. 下图是由哪个平面图形旋转得到的（    ）

A.  B.  C.  D.

【答案】A

【解析】

【分析】

根据圆柱、圆锥与圆台的定义，判断选项中的图形旋转一周后所得到的几何体的形状，进而可得结果.

【详解】解：B中图形旋转得到两个相同底面的圆锥，不合题意；

C中图形旋转得到相同底面的圆柱与圆锥，不合题意；

D中图形旋转得到两个圆锥与一个圆柱，不合题意；

A中图形旋转得到一个圆台与一个圆锥，合题意.

故选：A.

【点睛】本题主要考查旋转体的基本定义，考查了空间想象能力，属于基础题.

2. 下列命题中：①，；②，；③；④；正确命题的个数是（    ）

A. 1 B. 2 C. 3 D. 4

【答案】C

【解析】

【分析】

①利用不等式的加法法则判断；②可以举反例判断；③利用不等式性质判断；④可以利用作差法判断.

【详解】①，由不等式的加法得，所以该命题正确；

②，是错误的，如：，满足已知，但是不满足，所以该命题错误；

③，所以，所以该命题正确；

④所以，所以该命题正确.

故选：C

【点睛】本题主要考查不等式的性质，考查不等式真假命题的判断，意在考查学生对这些知识的理解掌握水平，属于基础题.

3. 不等式的解集为（    ）

A.  B. 或

C. 或 D.

【答案】B

【解析】

【分析】

直接解出即可.

【详解】由可得，所以或

故选：B

【点睛】本题考查的是一元二次不等式的解法，较简单.

4. 有一个几何体的三视图如图所示，这个几何体是一个　(　　)

A. 棱台 B. 棱锥 C. 棱柱 D. 都不对

【答案】A

【解析】

由三视图可知此几何体是一个四棱台．

5. 在中，，则∠等于(　　)

A. 30°或150° B. 60° C. 60°或120° D. 30°

【答案】C

【解析】

【分析】

直接使用正弦定理，即可求得结果.

【详解】根据正弦定理，

可得，解得，故可得为60°或120°；

又，则，显然两个结果都满足题意.

故选：C.

【点睛】本题考查正弦定理的直接使用，属基础题.

6. 直角坐标系内的一动点，运动时该点坐标满足不等式，则这个动点的运动区域(用阴影表示)是（     ）

A.  B.

C.  D.

【答案】A

【解析】

【分析】

结合所给的不等式首先确定其所表示的区域，然后结合选项确定正确选项即可.

【详解】由题意可知，表示直线上方区域，结合所给的选项，只有A选项符合题意.

故选A.

【点睛】本题主要考查不等式所表示的平面区域的确定，属于基础题.

7. 无穷数列1,3,6,10，…的通项公式为（ ）

A.  B.

C.  D.

【答案】C

【解析】

试题分析：由累加法得:,分别相加得,

,故选C.

考点：数列的通项公式.

8. 2008是等差数列的4，6，8，…中的（    ）

A. 第1000项 B. 第1001项 C. 第1002项 D. 第1003项

【答案】D

【解析】

【分析】

由等差数列的前3项可得通项公式，然后列方程求解即可.

【详解】因为等差数列的前3项分别为4，6，8，

所以，

所以，

由，

故选：D.

【点睛】本题主要考查等差数列的通项公式，意在考查对基础知识的掌握情况，属于基础题.

9. 在等差数列{an}中，已知a1+a2+a3+a4+a5＝20，那么a3＝（    ）

A. 4 B. 5 C. 6 D. 7

【答案】A

【解析】

【分析】

根据等差数列的性质，得，代入可得选项.

【详解】根据等差数列的性质，得，，所以.

故选：A.

【点睛】本题主要考查等差数列的性质,关键在于观察数列的项的脚标的特殊关系，属于基础题.

10. 数列，，若，，则（ ）

A.  B.

C. 48 D. 94

【答案】B

【解析】

试题分析：,,又,数列是以为首项,公比为的等比数列,根据等比数列的通项公式得,,故选B.

考点：等比数列的通项公式.

11. 已知x，y满足，则的最大值是（    ）

A. 1 B. 2 C. 3 D. 4

【答案】D

【解析】

【分析】

由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，把最优解的坐标代入目标函数得结论.

【详解】画出表示的可行域，如图，

将变形为，

平移直线，

由图可知当直经过点时，

直线在轴上的截距最小，

此时最大值为，

故选：D.

【点睛】本题主要考查线性规划中，利用可行域求目标函数的最值，属于简单题.求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.

12. 在等比数列中，若前10项的和，若前20项的和，则前30项的和（    ）

A. 60 B. 70 C. 80 D. 90

【答案】B

【解析】

【分析】

由等比数列的性质可得，成等比数列，即，代入可求．

【详解】由等比数列的性质可得, 成等比数列，

，

故选：B．

【点睛】本题主要考查等比数列的性质，意在考查灵活应用所学知识解答问题的能力，属于基础题.

第Ⅱ卷（非选择题  共90分）

二.填空题：本大题共4个小题，每小题5分，共20分.

13. 黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案：

则第个图案中有白色地面砖                  块.

【答案】4n+2

【解析】

解：观察、分析图案，得到规律，第1个、第2个，第3个…个图案有白色地板砖分别是6，10，14…个，组成一个

公差是4，首项为6的等差数列．

因此第n个图案中有白色地面砖有6+（n-1）×4=6+4n-4=4n+2．

故答案为4n+2．

14. 当时，的最小值为______.

【答案】

【解析】

【分析】

将所求代数式变形为，然后利用基本不等式可求得所求代数式的最小值.

【详解】，，由基本不等式得.

当且仅当时，等号成立.

因此，的最小值为.

故答案为：.

【点睛】本题考查利用基本不等式求代数式的最值，考查计算能力，属于基础题.

15. 若的面积为，则内角C等于______.

【答案】

【解析】

【分析】

利用余弦定理以及三角形面积公式可得，从而可得结果.

【详解】由余弦定理可得

因为的面积为，

所以，

可得，

因为，所以，

故答案为：.

【点睛】应用余弦定理，一定要熟记两种形式：（1）；（2），同时还要熟练掌握运用两种形式条件.另外，在解与三角形、三角函数有关的问题时，还需要记住等特殊角的三角函数值，以便在解题中直接应用.

16. 定义一种新运算：，若关于x的不等式：有解，则a的取值范围是______.

【答案】

【解析】

【分析】

根据题中定义的运算，化简原不等式为一元二次不等式，利用判别式大于零可得结果.

【详解】因为，

所以化为，

即，

要使有解，

只需

解得或，

故答案为：.

【点睛】遇到新定义问题，应耐心读题，分析新定义的特点，弄清新定义的性质，按新定义的要求，“照章办事”，逐条分析、验证、运算，使问题得以解决.

三.解答题：本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤.

17. 已知不等式的解集为．

（1）求和的值；

（2）求不等式的解集.

【答案】(1)，；(2)．

【解析】

【详解】试题分析：(1)由不等式的解集为，可知和是一元二次方程的两根，利用韦达定理列出方程组，即可求解和的值；(2)由（1）知所求不等式即为，确定方程的两根，即可求解不等式的解集.

试题解析：（1）由不等式的解集为，

可知2和1是一元二次方程的两根，

所以，即，

（2）由（1）知所求不等式即为

方程式的两根分别是1和，

所以所求不等式的解集为

考点：一元二次不等式问题.

18. 设{an}是公比为正数的等比数列a1=2，a3=a2+4．

（Ⅰ）求{an}的通项公式；

（Ⅱ）设{bn}是首项为1，公差为2的等差数列，求数列{an+bn}的前n项和Sn．

【答案】（Ⅰ）an=2×2n﹣1=2n（Ⅱ）2n﹣1 2n+1﹣2+n2=2n+1+n2﹣2

【解析】

试题分析：（Ⅰ）由{an}是公比为正数的等比数列，设其公比，然后利用a1=2，a3=a2+4可求得q，即可求得{an}的通项公式

（Ⅱ）由{bn}是首项为1，公差为2的等差数列 可求得bn=1+（n﹣1）×2=2n﹣1，然后利用等比数列与等差数列的前n项和公式即可求得数列{an+bn}的前n项和Sn．

解：（Ⅰ）∵设{an}是公比为正数的等比数列

∴设其公比为q，q＞0

∵a3=a2+4，a1=2

∴2×q2="2×q+4" 解得q=2或q=﹣1

∵q＞0

∴q="2"

∴{an}的通项公式为an=2×2n﹣1=2n

（Ⅱ）∵{bn}是首项为1，公差为2的等差数列

∴bn=1+（n﹣1）×2=2n﹣1

∴数列{an+bn}的前n项和Sn=+=2n+1﹣2+n2=2n+1+n2﹣2

点评：本题考查了等比数列的通项公式及数列的求和，注意题目条件的应用．在用等比数列的前n项和公式时注意辨析q是否为1，只要简单数字运算时不出错，问题可解，是个基础题．

19. 设是等差数列，，且成等比数列.

（1）求的通项公式

（2）求数列的前项和

【答案】（1）（2）

【解析】

【分析】

(1)首先可以根据成等比数列以及列出算式并通过计算得出公差，然后根据等差数列的通项公式即可得出结果；

(2)本题可结合(1)中结论以及等差数列的前和公式即可得出结果．

【详解】(1)因为，且成等比例，

所以，解得.

所以.

(2)因为，所以.

【点睛】本题考查等比中项、等差数列的通项公式以及等差数列的前和公式，等差数列的通项公式为，等差数列的前和公式为，考查计算能力，是中档题．

20. 已知a，b，c分别为三个内角A，B，C的对边，且.

（1）求角的大小；

（2）若，且的面积为，求a的值.

【答案】(Ⅰ)；(Ⅱ)

【解析】

【分析】

（Ⅰ）由题意结合正弦定理边化角，整理计算可得，则.

（Ⅱ）由三角形面积公式可得：，结合余弦定理计算可得，则.

【详解】（Ⅰ）由正弦定理得，，

∵，

∴，即．

∵∴，

∴∴．

（Ⅱ）由：可得．

∴，

∵，

∴由余弦定理得：，

∴.

【点睛】在处理三角形中的边角关系时，一般全部化为角的关系，或全部化为边的关系．题中若出现边的一次式一般采用到正弦定理，出现边的二次式一般采用到余弦定理．应用正、余弦定理时，注意公式变式的应用．解决三角形问题时，注意角的限制范围．

21. 已知数列的前项和为，.

（1）求的通项公式

（2）若，求数列的前项和.

【答案】（1）（2）

【解析】

【分析】

（1）先计算出，然后由求出，再看是否与相符，相符就是一个表达式，不相符就用分段函数形式表示；

（2）用错位相减法求数列的前项和．

【详解】（1）由得：，因为，解得

由知，

两式相减得

因为，所以，即

因此是首项为，公比为等比数列

所以

（2）由（1）知，所以数列前项和为：

…①

则 …②

②-①得

【点睛】本题考查已知前项和和关系求数列的通项公式，考查用错位相减法求数列的和．在已知和的关系求数列的通项公式时，要注意与后面的（）的求法是不相同的，即中，而．

22. 如图，CM，CN为某公园景观湖胖的两条木栈道，∠MCN=120°，现拟在两条木栈道的A，B处设置观景台，记BC=a，AC=b，AB=c（单位：百米）

（1）若a，b，c成等差数列，且公差为4，求b的值；

（2）已知AB=12，记∠ABC=θ，试用θ表示观景路线A-C-B的长，并求观景路线A-C-B长的最大值．

【答案】（1）10；（2）8.

【解析】

【分析】

（1）利用a、b、c成等差数列,且公差为4,可得,利用余弦定理即可求b的值；

（2）利用正弦定理,求出AC、BC,可得到观景路线A-C-B为是关于的函数,求出最大值即可

【详解】解：（1）∵a、b、c成等差数列,且公差为4,∴,

∵∠MCN=120°，

∴,即°,

∴b=10

（2）由题意,在中,,

则,

∴,,

∴观景路线A-C-B的长,且,

∴θ=30°时,观景路线A-C-B长的最大值为8

【点睛】本题考查利用余弦定理求三角形的边,考查正弦定理的应用,考查三角函数的最值问题,考查运算能力