江苏省高考数学模拟试卷

这是一份江苏省高考数学模拟试卷，共22页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。

江苏省高考数学模拟试卷3
一、填空题：本大题共14小题，每小题5分，共70分．
1．设集合U={1，2，3，4}，A={1，2}，B={2，4}，则∁U（A∩B）等于　　　　　　．
2．已知b∈R，若（2+bi）（2﹣i）为纯虚数，则|1+bi|=　　　　　　．
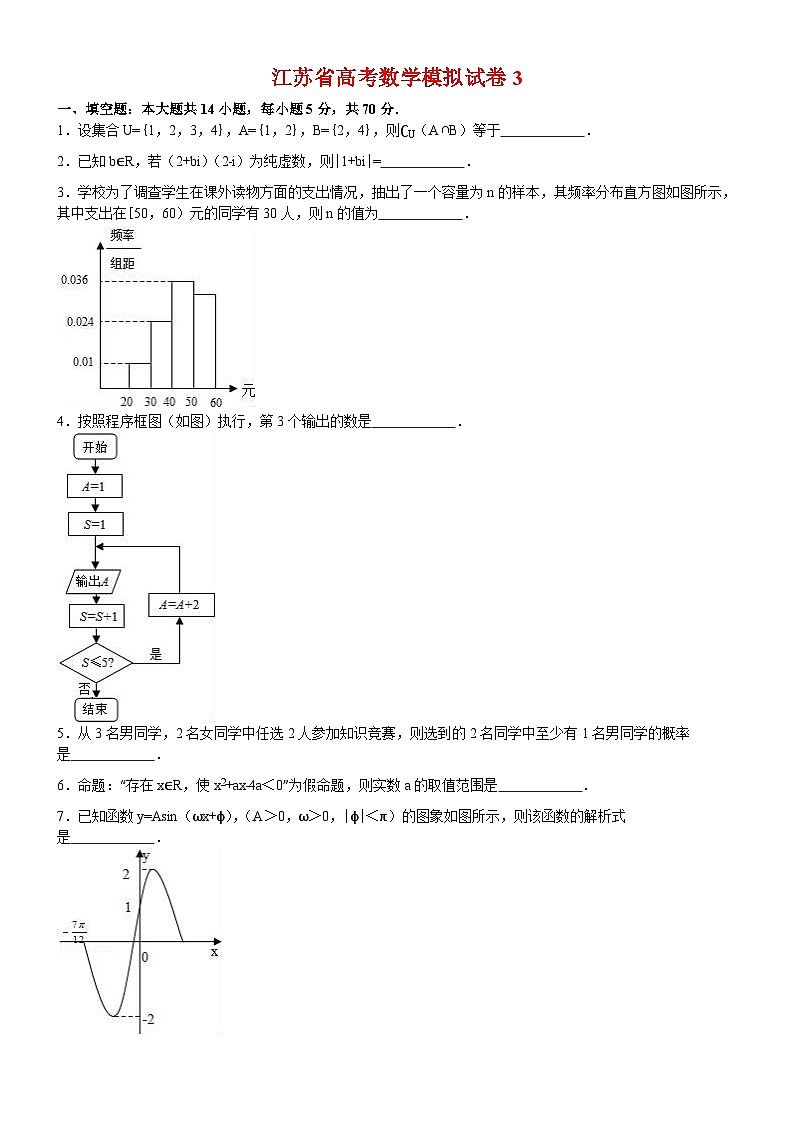
3．学校为了调查学生在课外读物方面的支出情况，抽出了一个容量为n的样本，其频率分布直方图如图所示，其中支出在[50，60）元的同学有30人，则n的值为　　　　　　．

4．按照程序框图（如图）执行，第3个输出的数是　　　　　　．

5．从3名男同学，2名女同学中任选2人参加知识竞赛，则选到的2名同学中至少有1名男同学的概率是　　　　　　．
6．命题：“存在x∈R，使x2+ax﹣4a＜0”为假命题，则实数a的取值范围是　　　　　　．
7．已知函数y=Asin（ωx+φ），（A＞0，ω＞0，|φ|＜π）的图象如图所示，则该函数的解析式是　　　　　　．

8．如图，四边形OABC是边长为1的正方形，点D在OA的延长线上，且OD=2，点P为△BCD内（含边界）的动点，设=α+β（α，β∈R），则α+β的最大值等于
　　　　　　．

9．如图，在长方体ABCD﹣A1B1C1D1中，对角线B1D与平面A1BC1交于E点．记四棱锥E﹣A1B1C1D1的体积为V1，长方体ABCD﹣A1B1C1D1的体积为V2，则的值是　　　　　　．

10．若曲线：y=ax+1（a＞0且a≠1）在点（0，2）处的切线与直线x+2y+1=0垂直，则a=　　　　　　．
11．实数x，y满足4x2﹣5xy+4y2=5，设 S=x2+y2，则+=　　　　　　．
12．设函数f（x）=，则满足f（f（a））=2（f（a））2的a的取值范围为　　　　　　．
13．已知圆O：x2+y2=1，点C为直线l：2x+y﹣2=0上一点，若圆O存在一条弦AB垂直平分线段OC，则点C的横坐标的取值范围是　　　　　　．
14．各项均为正偶数的数列a1，a2，a3，a4中，前三项依次成公差为d（d＞0）的等差数列，后三项依次成公比为q的等比数列，若a4﹣a1=88，则q的所有可能的值构成的集合为　　　　　　．
　
二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答，解答时写出文字说明、证明过程或演算步骤．
15．已知α，β均为锐角，且，．
（1）求sin（α﹣β）的值；
（2）求cosβ的值．
16．已知三棱柱ABC﹣A1B1C1中，CC1⊥底面ABC，AB=AC=AA1=2，∠BAC=90°，D，E，F分别为B1A，C1C，BC的中点．
（I）求证：DE∥平面ABC；
（II）平面AEF⊥平面BCC1B1；求三棱锥A﹣BCB1的体积．

17．如图，有一直径为8米的半圆形空地，现计划种植甲、乙两种水果，已知单位面积种植水果的经济价值是种植乙水果经济价值的5倍，但种植甲水果需要有辅助光照．半圆周上的C处恰有一可旋转光源满足甲水果生产的需要，该光源照射范围是∠ECF=，点E，F的直径AB上，且∠ABC=．
（1）若CE=，求AE的长；
（2）设∠ACE=α，求该空地产生最大经济价值时种植甲种水果的面积．

18．已知椭圆C方程为+=1（a＞n＞0），离心率e=，过焦点且与长轴垂直的直线被椭圆所截得线段长为1．
（1）求椭圆C方程；
（2）D，E，F为曲线C上的三个动点，D在第一象限，E，F关于原点对称，且|DE|=|DF|，问△DEF的面积是否存在最小值？若存在，求出此时D点的坐标；若不存在，请说明理由．
19．设a∈R，函数f（x）=lnx﹣ax．
（Ⅰ）求f（x）的单调递增区间；
（Ⅱ）设F（x）=f（x）+ax2+ax，问F（x）是否存在极值，若存在，请求出极值；若不存在，请说明理由；
（Ⅲ）设A（x1，y1），B（x2，y2）是函数g（x）=f（x）+ax图象上任意不同的两点，线段AB的中点为C（x0，y0），直线AB的斜率为为k．证明：k＞g′（x0）．
20．对于给定数列{cn}，如果存在实常数p，q，使得cn+1=pcn+q（p≠0）对于任意的n∈N*都成立，我们称这个数列{cn}是“M类数列”．
（1）若an=2n，bn=3•2n，n∈N*，判断数列{an}，{bn}是否为“M类数列”，并说明理由；
（2）若数列{an}是“M类数列”，则数列{an+an+1}、{an•an+1}是否一定是“M类数列”，若是的，加以证明；若不是，说明理由；
（3）若数列{an}满足：a1=1，an+an+1=3•2n（n∈N*），设数列{an}的前n项和为Sn，求Sn的表达式，并判断{an}是否是“M类数列”．
　
选做题[选修4-1：几何证明选讲](任选两个)
21．如图所示，已知⊙O1与⊙O2相交于A、B两点，过点A作⊙O1的切线交⊙O2于点C，过点B作两圆的割线，分别交⊙O1、⊙O2于点D、E，DE与AC相交于点P．
（1）求证：AD∥EC；
（2）若AD是⊙O2的切线，且CA=8，PC=2，BD=9，求AD的长．

　
[选修4-2：矩阵与变换]
22．已知线性变换T1是按逆时针方向旋转90°的旋转变换，其对应的矩阵为M，线性变换T2：对应的矩阵为N．
（Ⅰ）写出矩阵M、N；
（Ⅱ）若直线l在矩阵NM对应的变换作用下得到方程为y=x的直线，求直线l的方程．
　
[选修4-4：坐标系与参数方程选讲]
23．已知在平面直角坐标系xOy中，直线l的参数方程是（t是参数），以原点O为极点，x轴正半轴为极轴建立极坐标，曲线C的极坐标方程．
（Ⅰ）判断直线l与曲线C的位置关系；
（Ⅱ）设M为曲线C上任意一点，求x+y的取值范围．
　
[选修4-5：不等式选讲]
24．设函数f（x）=|2x+1|﹣|x﹣2|．
（1）求不等式f（x）＞2的解集；
（2）∀x∈R，使f（x）≥t2﹣t，求实数t的取值范围．
　
解答题
25．网上购物逐步走进大学生活，某大学学生宿舍4人积极参加网购，大家约定：每个人通过掷一枚质地均匀的骰子决定自己去哪家购物，掷出点数为5或6的人去淘宝网购物，掷出点数小于5的人去京东商场购物，且参加者必须从淘宝和京东商城选择一家购物．
（Ⅰ）求这4人中恰有1人去淘宝网购物的概率；
（Ⅱ）用ξ、η分别表示这4人中去淘宝网和京东商城购物的人数，记X=ξη，求随机变量X的分布列与数学期望EX．
26．记（1+）（1+）…（1+）的展开式中，x的系数为an，x2的系数为bn，其中n∈N*．
（1）求an；
（2）是否存在常数p，q（p＜q），使bn=（1+）（1+） 对n∈N*，n≥2恒成立？证明你的结论．
　
江苏省高考数学模拟试卷试题解析
一、填空题：本大题共14小题，每小题5分，共70分．
1．设集合U={1，2，3，4}，A={1，2}，B={2，4}，则∁U（A∩B）等于　{1，3，4}　．
【考点】补集及其运算．
【分析】首先求出A∩B，然后对其进行补集运算．
【解答】解：由已知，A∩B={2}，所以∁U（A∩B）={1，3，4}；
故答案为：{1，3，4}．
2．已知b∈R，若（2+bi）（2﹣i）为纯虚数，则|1+bi|=　　．
【考点】复数求模．
【分析】利用纯虚数的定义、模的计算公式即可得出．
【解答】解：（2+bi）（2﹣i）=4+b+（2b﹣2）i为纯虚数，
∴，解得b=﹣4．
则|1+bi|=|1﹣4i|==．
故答案为：．
3．学校为了调查学生在课外读物方面的支出情况，抽出了一个容量为n的样本，其频率分布直方图如图所示，其中支出在[50，60）元的同学有30人，则n的值为　100　．

【考点】频率分布直方图．
【分析】根据频率直方图的意义，由前三个小组的频率可得样本在[50，60）元的频率，计算可得样本容量．
【解答】解：由题意可知：前三个小组的频率之和=（0.01+0.024+0.036）×10=0.7，
∴支出在[50，60）元的频率为1﹣0.7=0.3，
∴n的值=；
故答案100．
4．按照程序框图（如图）执行，第3个输出的数是　5　．

【考点】循环结构．
【分析】根据所给的循环结构知第一个输出的数字是1，第二个输出的数字是1+2=3，第三个输出的数字是3+2=5．
【解答】解：由题意知第一个输出的数字是1
第二个输出的数字是1+2=3
第三个输出的数字是3+2=5
故答案为：5
　
5．从3名男同学，2名女同学中任选2人参加知识竞赛，则选到的2名同学中至少有1名男同学的概率是　　．
【考点】古典概型及其概率计算公式．
【分析】选到的2名同学中至少有1名男同学的对立事件是选到两名女同学，由此利用对立事件概率计算公式能求出选到的2名同学中至少有1名男同学的概率．
【解答】解：从3名男同学，2名女同学中任选2人参加知识竞赛，
基本事件总数n==10，
选到的2名同学中至少有1名男同学的对立事件是选到两名女同学，
∴选到的2名同学中至少有1名男同学的概率：
p=1﹣=．
故答案为：．
　
6．命题：“存在x∈R，使x2+ax﹣4a＜0”为假命题，则实数a的取值范围是　[﹣16，0]　．
【考点】命题的真假判断与应用．
【分析】将条件转化为x2+ax﹣4a≥0恒成立，必须△≤0，从而解出实数a的取值范围．
【解答】解：命题：“存在x∈R，使x2+ax﹣4a＜0”为假命题，
即x2+ax﹣4a≥0恒成立，必须△≤0，
即：a2+16a≤0，解得﹣16≤a≤0，
故实数a的取值范围为[﹣16，0]．
故答案为：[﹣16，0]．
　
7．已知函数y=Asin（ωx+φ），（A＞0，ω＞0，|φ|＜π）的图象如图所示，则该函数的解析式是　y=2sin（x+）　．

【考点】由y=Asin（ωx+φ）的部分图象确定其解析式．
【分析】由图可知，A=2，由点（0，1）在函数的图象上，可得sinφ=，利用五点作图法可解得φ，又点（﹣，0）在函数的图象上，可得﹣ω+=kπ，k∈Z，进而解得ω，从而得解该函数的解析式．
【解答】解：∵由图知A=2，y=2sin（ωx+φ），
∵点（0，1），在函数的图象上，
∴2sinφ=1，解得：sinφ=，
∴利用五点作图法可得：φ=，
∵点（﹣，0），在函数的图象上，可得：2sin（﹣ω+）=0，
∴可得：﹣ω+=kπ，k∈Z，
解得：ω=﹣，k∈Z，
∵ω＞0，
∴当k=0时，ω=，
∴y=2sin（x+）．
故答案为：y=2sin（x+）．
　
8．如图，四边形OABC是边长为1的正方形，点D在OA的延长线上，且OD=2，点P为△BCD内（含边界）的动点，设=α+β（α，β∈R），则α+β的最大值等于
　　．

【考点】简单线性规划；平面向量的基本定理及其意义．
【分析】因为是正方形，所以可考虑建立平面直角坐标系：以O为原点，OA，OC所在直线分别为x轴，y轴建立平面直角坐标系，这时候可求出，所以设P（x，y），所以根据已知条件可得：（x，y）=（2β，α），所以可用x，y表示α，β，并得到，这样求的最大值即可．而x，y的取值范围便是△BCD上及其内部，所以可想着用线性规划的知识求解．所以设z=，y=，所以z表示直线在y轴上的截距，要求α+β的最大值，只需求截距z的最大值即可，而通过图形可看出当该直线过B点时截距最大，所以将B点坐标带入直线方程，即可得到z的最大值，即α+β的最大值．
【解答】解：分别以边OA，OC所在直线为x，y轴建立如图所实施平面直角坐标系；
则：，设P（x，y），；
∴（x，y）=α（0，1）+β（2，0）=（2β，α）；
∴；
∴；
设z=，则：y=，所以z是直线y=在y轴上的截距；
由图形可以看出，当该直线经过B（1，1）点时，它在y轴的截距z最大，最大为；
∴α+β的最大值是．
故答案为：．
　
9．如图，在长方体ABCD﹣A1B1C1D1中，对角线B1D与平面A1BC1交于E点．记四棱锥E﹣A1B1C1D1的体积为V1，长方体ABCD﹣A1B1C1D1的体积为V2，则的值是　　．

【考点】棱柱、棱锥、棱台的体积．
【分析】连接B1D1∩A1C1=F，证明以E是△A1BC1的重心，那么点E到平面A1B1C1D1的距离是BB1的，利用体积公式，即可得出结论．
【解答】解：连接B1D1∩A1C1=F，平面A1BC1∩平面BDD1B1=BF，
因为E∈平面A1BC1，E∈平面BDD1B1，所以E∈BF，
连接BD，因为F是A1C1的中点，所以BF是中线，
又根据B1F平行且等于BD，所以=，
所以E是△A1BC1的重心，那么点E到平面A1B1C1D1的距离是BB1的，
所以V1=×BB1，
而V2=×BB1，
所以=．
故答案为：．

　
10．若曲线：y=ax+1（a＞0且a≠1）在点（0，2）处的切线与直线x+2y+1=0垂直，则a=　e2　．
【考点】利用导数研究曲线上某点切线方程．
【分析】求出函数的导数，求得切线的斜率，由两直线垂直的条件：斜率之积为﹣1，可得a的方程，即可解得a．
【解答】解：y=ax+1的导数为y′=axlna，
即有曲线在点（0，2）处的切线斜率为k=lna，
由于切线与直线x+2y+1=0垂直，
则lna•（﹣）=﹣1，
解得a=e2，
故答案为：e2．
　
11．实数x，y满足4x2﹣5xy+4y2=5，设 S=x2+y2，则+=　　．
【考点】基本不等式．
【分析】由2xy≤x2+y2可得5xy=4x2+4y2﹣5≤（x2+y2），从而可求s的最大值，由x2+y2≥﹣2xy及5xy=4x2+4y2﹣5≥﹣8xy﹣5可得xy的范围，进而可求s的最小值，代入可求
【解答】解：∵4x2﹣5xy+4y2=5，
∴5xy=4x2+4y2﹣5，
又∵2xy≤x2+y2
∴5xy=4x2+4y2﹣5≤（x2+y2）
设 S=x2+y2，
4s﹣5≤s
∴s即
∵x2+y2≥﹣2xy
∴5xy=4x2+4y2﹣5≥﹣8xy﹣5
∴xy
∴﹣xy
∴S=x2+y2≥﹣2xy
∴
∴+==
故答案为：
　
12．设函数f（x）=，则满足f（f（a））=2（f（a））2的a的取值范围为　[，+∞）∪{}　．
【考点】分段函数的应用．
【分析】令f（a）=t，则f（t）=2t2，讨论t＜1，及t≥1时，以及a＜1，a≥1，由分段函数的解析式，解不等式或方程即可得到所求范围．
【解答】解：令f（a）=t，
则f（t）=2t2，
若t＜1时，由f（t）=2t2得3t﹣1=2t2，即2t2﹣3t+1=0，得t=1（舍）或t=，
当t≥1时，2t2=2t2成立，
即t≥1或t=，
若a＜1，由f（a）≥1，即3a﹣1≥1，解得a≥，且a＜1；此时≤a＜1，
由f（a）=得3a﹣1=得a=，满足条件，
若a≥1，由f（a）≥1，即2a2≥1，
∵a≥1，∴此时不等式2a2≥1恒成立，
由f（a）=得2a2=得a=±，不满足条件，
综上≤a＜1或a≥1．即a≥．
综上可得a的范围是a≥或a=．
故答案为：[，+∞）∪{}
　
13．已知圆O：x2+y2=1，点C为直线l：2x+y﹣2=0上一点，若圆O存在一条弦AB垂直平分线段OC，则点C的横坐标的取值范围是　（0，）　．
【考点】直线与圆相交的性质．
【分析】设C（x0，2﹣2x0），得线段OC的中点坐标，则只要中点能落在圆的内部，就存在弦AB垂直平分线段OC，所以代入圆的方程，即可确定点C的横坐标的取值范围．
【解答】解：设C（x0，2﹣2x0），则线段OC的中点坐标是D（x0，1﹣x0），则只要中点能落在圆的内部，就存在弦AB垂直平分线段OC，所以代入圆的方程，（ x0）2+（1﹣x0）2＜1，解得0＜x0＜．
故答案为：（0，）．
　
14．各项均为正偶数的数列a1，a2，a3，a4中，前三项依次成公差为d（d＞0）的等差数列，后三项依次成公比为q的等比数列，若a4﹣a1=88，则q的所有可能的值构成的集合为　{}　．
【考点】等差数列与等比数列的综合．
【分析】先假设数列的项，利用三项依次成公比为q的等比数列，建立等式，从而可得公差的范围及取值，由此，即可求得结论．
【解答】解：设a1，a1+d，a1+2d，a1+88，其中a1，d均为正偶数，则
∵后三项依次成公比为q的等比数列
∴，
整理得，所以（d﹣22）（3d﹣88）＜0，即，
则d可能为24，26，28，
当d=24时，a1=12，；当d=26时，（舍去）；当d=28时，a1=168，；
所以q的所有可能值构成的集合为．
故答案为
　
二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答，解答时写出文字说明、证明过程或演算步骤．
15．已知α，β均为锐角，且，．
（1）求sin（α﹣β）的值；
（2）求cosβ的值．
【考点】两角和与差的正切函数；同角三角函数间的基本关系；两角和与差的正弦函数．
【分析】（1）根据α、β的范围，利用同角三角函数的基本关系，求得sin（α﹣β）的值．
（2）由（1）可得，，，根据cosβ=cos[α﹣（α﹣β）]，利用两角差的余弦公式求得结果．
【解答】解：（1）∵，从而．
又∵，∴． …
利用同角三角函数的基本关系可得sin2（α﹣β）+cos2（α﹣β）=1，且，
解得． …
（2）由（1）可得，．∵α为锐角，，∴． …
∴cosβ=cos[α﹣（α﹣β）]=cosαcos（α﹣β）+sinαsin（α﹣β）…
==． …
　
16．已知三棱柱ABC﹣A1B1C1中，CC1⊥底面ABC，AB=AC=AA1=2，∠BAC=90°，D，E，F分别为B1A，C1C，BC的中点．
（I）求证：DE∥平面ABC；
（II）平面AEF⊥平面BCC1B1；求三棱锥A﹣BCB1的体积．

【考点】平面与平面之间的位置关系；直线与平面平行的判定．
【分析】（1）欲证DE∥平面ABC，根据线面平行的判定定理可知，证线线平行，取AB中点G，连DG，CG，只需证DE∥GC即可；
（2）欲证平面AEF⊥平面BCC1B1，根据面面垂直的判定定理可知，证AF⊥平面BCC1B1即可，然后再根据体积公式求出三棱锥A﹣BCB1的体积．
【解答】解：（I）取AB中点G，连DG，CG
在三棱柱ABC﹣A1B1C1中，CC1⊥底面ABC，
∴BCC1B1是矩形．
∵D，E分别为AB1，CC1的中点，
∴，
∴是平行四边形，∴DE∥GC．
∵GC⊂平面ABC，DE⊄平面ABC，
∴DE∥平面ABC．

（II）三棱柱ABC﹣A1B1C1中，CC1⊥底面ABC，
∴AF⊥CC1∵AB=AC，F为BC中点，∴AF⊥BC
又BC∩CC1=C∴AF⊥平面BCC1B1，又AF⊂平面AEF，
∴平面AEF⊥平面BCC1B1
AF⊥平面BCC1B1，
在由已知，RT△ABC中，AB=AC=2，
∴BC=2，
∴

　
17．如图，有一直径为8米的半圆形空地，现计划种植甲、乙两种水果，已知单位面积种植水果的经济价值是种植乙水果经济价值的5倍，但种植甲水果需要有辅助光照．半圆周上的C处恰有一可旋转光源满足甲水果生产的需要，该光源照射范围是∠ECF=，点E，F的直径AB上，且∠ABC=．
（1）若CE=，求AE的长；
（2）设∠ACE=α，求该空地产生最大经济价值时种植甲种水果的面积．

【考点】函数模型的选择与应用．
【分析】（1）利用余弦定理，即可求AE的长；
（2）设∠ACE=α，求出CF，CE，利用S△CEF=，计算面积，求出最大值，即可求该空地产生最大经济价值时种植甲种水果的面积．
【解答】解：（1）由题意，△ACE中，AC=4，∠A=，CE=，
∴13=16+AE2﹣2×，
∴AE=1或3；
（2）由题意，∠ACE=α∈[0，]，∠AFC=π﹣∠A﹣∠ACF=﹣α．
在△ACF中，由正弦定理得，∴CF=；
在△ACE中，由正弦定理得，∴CE=，
该空地产生最大经济价值时，△CEF的面积最大，
S△CEF==，
∵α∈[0，]，∴0≤sin（2α+）≤1，
∴α=时，S△CEF取最大值为4，该空地产生最大经济价值．
　
18．已知椭圆C方程为+=1（a＞n＞0），离心率e=，过焦点且与长轴垂直的直线被椭圆所截得线段长为1．
（1）求椭圆C方程；
（2）D，E，F为曲线C上的三个动点，D在第一象限，E，F关于原点对称，且|DE|=|DF|，问△DEF的面积是否存在最小值？若存在，求出此时D点的坐标；若不存在，请说明理由．
【考点】椭圆的简单性质．
【分析】（1）由过焦点且与长轴垂直的直线被椭圆所截得线段长为1，可得=1，又e==，a2=b2+c2，联立解出即可得出．
（2）设直线EF的方程为：y=kx，则直线OD的方程为： x．（k≠0）．联立，解得，．可得：|EF|2=4（+）．同理可得：xD，yD．|OD|2．设△DEF的面积=S．可得S2=，化简利用二次函数的单调性即可得出．
【解答】解：（1）∵过焦点且与长轴垂直的直线被椭圆所截得线段长为1，
∴=1，又e==，a2=b2+c2，
联立解得a=2，b=1，c=．
∴椭圆C的方程为=1．
（2）设直线EF的方程为：y=kx，则直线OD的方程为： x．（k≠0）．
联立，解得=， =．
∴|EF|2=4（+）=．
同理可得：xD=，yD=．
|OD|2=．
设△DEF的面积=S．
∴S2==××==f（k），
令1+k2=t＞1，则f（k）==≥，
当且仅当t=8，k=﹣时取等号．
∴△DEF的面积存在最小值．
此时D．
　
19．设a∈R，函数f（x）=lnx﹣ax．
（Ⅰ）求f（x）的单调递增区间；
（Ⅱ）设F（x）=f（x）+ax2+ax，问F（x）是否存在极值，若存在，请求出极值；若不存在，请说明理由；
（Ⅲ）设A（x1，y1），B（x2，y2）是函数g（x）=f（x）+ax图象上任意不同的两点，线段AB的中点为C（x0，y0），直线AB的斜率为为k．证明：k＞g′（x0）．
【考点】利用导数研究函数的单调性；利用导数研究函数的极值．
【分析】（Ⅰ）先求出函数的定义域，求出函数f（x）的导函数，然后分类讨论，当a≤0时，f（x）的单调增区间为
（﹣∞，+∞），当a＞0时，f（x）的单调增区间为（0，）；
（Ⅱ）首先求出F（x）的导函数，然后分类讨论，当a≥0时，恒有F′（x）＞0，F（x）在（0，+∞）上无极值；当a＜0时，F（x）有极大值，无极小值；
（Ⅲ），又，求出g（x）的导函数，然后设出0＜x1＜x2，即证，再设，即证：，再进一步设出k（t），求出k（t）的导函数，则结论可证．
【解答】（Ⅰ）解：在区间（0，+∞）上，．
（1）当a≤0时，∵x＞0，∴f′（x）＞0恒成立，f（x）的单调增区间为（﹣∞，+∞）；
（2）当a＞0时，令f′（x）＞0，即，得．
∴f（x）的单调增区间为（0，）；
综上所述：
当a≤0时，f（x）的单调增区间为（﹣∞，+∞），
当a＞0时，f（x）的单调增区间为（0，）；
（Ⅱ）由F（x）=f（x）+ax2+ax=lnx﹣ax+ax2+ax=lnx+ax2
得 （ x＞0），
当a≥0时，恒有F′（x）＞0，
∴F（x）在（0，+∞）上无极值；
当a＜0时，令F′（x）=0，得，
x∈（0，），F′（x）＞0，F′（x）单调递增，
x∈（，+∞），F′（x）＜0，F′（x）单调递减．
∴．
F（x）无极小值．
综上所述：
a≥0时，F（x）无极值，
a＜0时，F（x）有极大值，无极小值；
（Ⅲ）证明：，
又，
∴g′（x0）=，
要证k＞g′（x0），即证，
不妨设0＜x1＜x2，即证，即证，
设，即证：，
也就是要证：，其中t∈（1，+∞），
事实上：设 t∈（1，+∞），
则=，
∴k（t）在（1，+∞）上单调递增，因此k（t）＞k（1）=0，即结论成立．
　
20．对于给定数列{cn}，如果存在实常数p，q，使得cn+1=pcn+q（p≠0）对于任意的n∈N*都成立，我们称这个数列{cn}是“M类数列”．
（1）若an=2n，bn=3•2n，n∈N*，判断数列{an}，{bn}是否为“M类数列”，并说明理由；
（2）若数列{an}是“M类数列”，则数列{an+an+1}、{an•an+1}是否一定是“M类数列”，若是的，加以证明；若不是，说明理由；
（3）若数列{an}满足：a1=1，an+an+1=3•2n（n∈N*），设数列{an}的前n项和为Sn，求Sn的表达式，并判断{an}是否是“M类数列”．
【考点】数列的应用．
【分析】（1）运用 M类数列定义判断，
（2）{an}是“M类数列”，得出an+1=pan+q，an+2=pan+1+q，求解an+1+an+2，an+1an+2的式子，结合定义判断即可
（3）整体运用an+an+1=3.2n（n∈N*），分类得出：当n为偶数时，Sn=3（2+23+…+2n﹣1）=2n+1﹣2，n为奇数时，Sn=1+3（22+24+…+2n﹣1）=2n+1﹣3，化简即可得出Sn，再运用反证法证明即可．
【解答】解：（1）因为an+1=an+2，p=1，q=2是“M类数列”，
bn+1=2bn，p=2，q=0是“M类数列”．
（2）因为{an}是“M类数列”，所以an+1=pan+q，an+2=pan+1+q，
所以an+1+an+2=p（an+1+an+2）+2q，因此，{an+an+1}是“M类数列”．
因为{an}是“M类数列”，所以an+1=pan+q，an+2=pan+1+q，
所以an+1an+2=p2（anan+1）+pq（an+an+1）+q2，
当q=0时，是“M类数列”；
当q≠0时，不是“M类数列”；
（3）当n为偶数时，Sn=3（2+23+…+2n﹣1）=2n+1﹣2，
当n为奇数时，Sn=1+3（22+24+…+2n﹣1）=2n+1﹣3，
所以Sn=．
当n为偶数时an=Sn﹣Sn﹣1=2n+1﹣2﹣（2n﹣3）=2n+1，
当n为奇数时，an=Sn﹣Sn﹣1=2n+1﹣3﹣（2n﹣2）=2n﹣1（n≥3），
所以an=
假设{an}是“M类数列”，
当n为偶数时，an+1=2n+1﹣1=pan+q=p（2n+1）+qp=2，q=﹣3，
当n为奇数时，an+1=2n+1+1=pan+q=p（2n﹣1）+q，
p=2，q=3，
得出矛盾，所以{an}不是“M类数列”．
　
选做题[选修4-1：几何证明选讲](任选两个)
21．如图所示，已知⊙O1与⊙O2相交于A、B两点，过点A作⊙O1的切线交⊙O2于点C，过点B作两圆的割线，分别交⊙O1、⊙O2于点D、E，DE与AC相交于点P．
（1）求证：AD∥EC；
（2）若AD是⊙O2的切线，且CA=8，PC=2，BD=9，求AD的长．

【考点】与圆有关的比例线段．
【分析】（1）连接AB，根据弦切角等于所夹弧所对的圆周角得到∠BAC=∠D，又根据同弧所对的圆周角相等得到∠BAC=∠E，等量代换得到∠D=∠E，根据内错角相等得到两直线平行即可；
（2）根据切割线定理得到PA2=PB•PD，求出PB的长，然后再根据相交弦定理得PA•PC=BP•PE，求出PE，再根据切割线定理得AD2=DB•DE=DB•（PB+PE），代入求出即可．
【解答】（1）证明：连接AB，
∵AC是⊙O1的切线，
∴∠BAC=∠D．
又∵∠BAC=∠E，∴∠D=∠E．
∴AD∥EC．
（2）解：如图，
∵PA是⊙O1的切线，PD是⊙O1的割线，
∴PA2=PB•PD，
PA=AC﹣PC=6，
即62=PB•（PB+9），
∴PB=3．
在⊙O2中，PA•PC=BP•PE．
∴PE=4．
∵AD是⊙O2的切线，DE是⊙O2的割线，
且DE=DB+BP+PE=9+3+4=16，
∴AD2=DB•DE=9×16，∴AD=12．

　
[选修4-2：矩阵与变换]
22．已知线性变换T1是按逆时针方向旋转90°的旋转变换，其对应的矩阵为M，线性变换T2：对应的矩阵为N．
（Ⅰ）写出矩阵M、N；
（Ⅱ）若直线l在矩阵NM对应的变换作用下得到方程为y=x的直线，求直线l的方程．
【考点】几种特殊的矩阵变换．
【分析】（Ⅰ）通过变换的特征即得结论；
（Ⅱ）由（I）得，通过题意可得，利用x′=y′计算即可．
【解答】解：（Ⅰ）通过题意，易得M=，N=；
（Ⅱ）由（I）得，
由=，
得，
由题意得x′=y′得3x=﹣2y，
∴直线l的方程为3x+2y=0．
　
[选修4-4：坐标系与参数方程选讲]
23．已知在平面直角坐标系xOy中，直线l的参数方程是（t是参数），以原点O为极点，x轴正半轴为极轴建立极坐标，曲线C的极坐标方程．
（Ⅰ）判断直线l与曲线C的位置关系；
（Ⅱ）设M为曲线C上任意一点，求x+y的取值范围．
【考点】简单曲线的极坐标方程；参数方程化成普通方程．
【分析】（Ⅰ）由直线的参数方程消去t得直线的直角坐标方程，化圆的极坐标方程为直角坐标方程，再由圆心到直线的距离与圆的半径的关系得到直线与圆的位置关系；
（Ⅱ）设出曲线C上的点的参数方程，由x+y=sinθ+cosθ，利用两角和的正弦化简后可得x+y的取值范围．
【解答】解：（Ⅰ）由，消去t得：y=x+．
由，得，即，
∴，即．
化为标准方程得：．
圆心坐标为，半径为1，圆心到直线x﹣y+=0的距离d=＞1．
∴直线l与曲线C相离；
（Ⅱ）由M为曲线C上任意一点，可设，
则x+y=sinθ+cosθ=，
∴x+y的取值范围是．
　
[选修4-5：不等式选讲]
24．设函数f（x）=|2x+1|﹣|x﹣2|．
（1）求不等式f（x）＞2的解集；
（2）∀x∈R，使f（x）≥t2﹣t，求实数t的取值范围．
【考点】一元二次不等式的应用；分段函数的解析式求法及其图象的作法；函数的最值及其几何意义．
【分析】（1）根据绝对值的代数意义，去掉函数f（x）=|2x+1|﹣|x﹣2|中的绝对值符号，求解不等式f（x）＞2，
（2）由（1）得出函数f（x）的最小值，若∀x∈R，恒成立，只须即可，求出实数t的取值范围．
【解答】解：（1）
当，∴x＜﹣5
当，∴1＜x＜2
当x≥2，x+3＞2，x＞﹣1，∴x≥2
综上所述{x|x＞1或x＜﹣5}．
（2）由（1）得，若∀x∈R，恒成立，
则只需，
综上所述．
　
解答题
25．网上购物逐步走进大学生活，某大学学生宿舍4人积极参加网购，大家约定：每个人通过掷一枚质地均匀的骰子决定自己去哪家购物，掷出点数为5或6的人去淘宝网购物，掷出点数小于5的人去京东商场购物，且参加者必须从淘宝和京东商城选择一家购物．
（Ⅰ）求这4人中恰有1人去淘宝网购物的概率；
（Ⅱ）用ξ、η分别表示这4人中去淘宝网和京东商城购物的人数，记X=ξη，求随机变量X的分布列与数学期望EX．
【考点】离散型随机变量的期望与方差；离散型随机变量及其分布列．
【分析】（Ⅰ）依题意，这4个人中，每个人去淘宝网购物的概率为，去京东网购物的概率为，设“这4个人中恰有i个人去淘宝网购物”为事件Ai，则，（i=0，1，2，3，4），由此能求出这4个人中恰有1人去淘宝网购物的概率．
（Ⅱ）由已知得X的所有可能取值为0，3，4，P（X=0）=P（A0）+P（A4），P（X=3）=P（A1）+P（A3），P（X=4）=P（A2），由此能求出X的分布列和EX．
【解答】解：（Ⅰ）依题意，这4个人中，每个人去淘宝网购物的概率为，去京东网购物的概率为，
设“这4个人中恰有i个人去淘宝网购物”为事件Ai（i=0，1，2，3，4），
则，（i=0，1，2，3，4），
这4个人中恰有1人去淘宝网购物的概率=．
（Ⅱ）由已知得X的所有可能取值为0，3，4，
P（X=0）=P（A0）+P（A4）==，
P（X=3）=P（A1）+P（A3）=+=，
P（X=4）=P（A2）==，
∴X的分布列为：
X
0
3
4
P



∴EX==．
　
26．记（1+）（1+）…（1+）的展开式中，x的系数为an，x2的系数为bn，其中n∈N*．
（1）求an；
（2）是否存在常数p，q（p＜q），使bn=（1+）（1+） 对n∈N*，n≥2恒成立？证明你的结论．
【考点】数学归纳法．
【分析】（1）根据多项式乘法运算法则，可得an=++…+，利用等比数列的求和公式，可得结论；
（2）先计算b2，b3的值，代入bn=（1+）（1+），解得p=﹣2，q=﹣1，再用数学归纳法证明．
【解答】解：（1）根据多项式乘法运算法则，得an=++…+=1﹣．…
（2）计算得b2=，b3=．
代入bn=（1+）（1+），解得p=﹣2，q=﹣1． …
下面用数学归纳法证明bn=（1﹣）（1﹣）=﹣+×（n≥2）：
①当n=2时，b2=，结论成立．
②设n=k时成立，即bk=﹣+×．
则当n=k+1时，bk+1=bk+=﹣+×+﹣=﹣+×．
由①②可得结论成立．　　　 …