2021-2022学年江苏省淮安市高一（上）期末数学试卷

2021-2022学年江苏省淮安市高一（上）期末数学试卷

一、单项选择题：本大题共8小题，每小题5分，共计40分，在每小题给出的四个选项中，只有一项是符合题目要求的．

1．（5分）已知集合，集合，则　　

A．，1， B．， C． D．

2．（5分）下列角中与终边相同的角是　　

A． B． C． D．

3．（5分）已知实数，，，则实数，，的大小是　　

A． B． C． D．

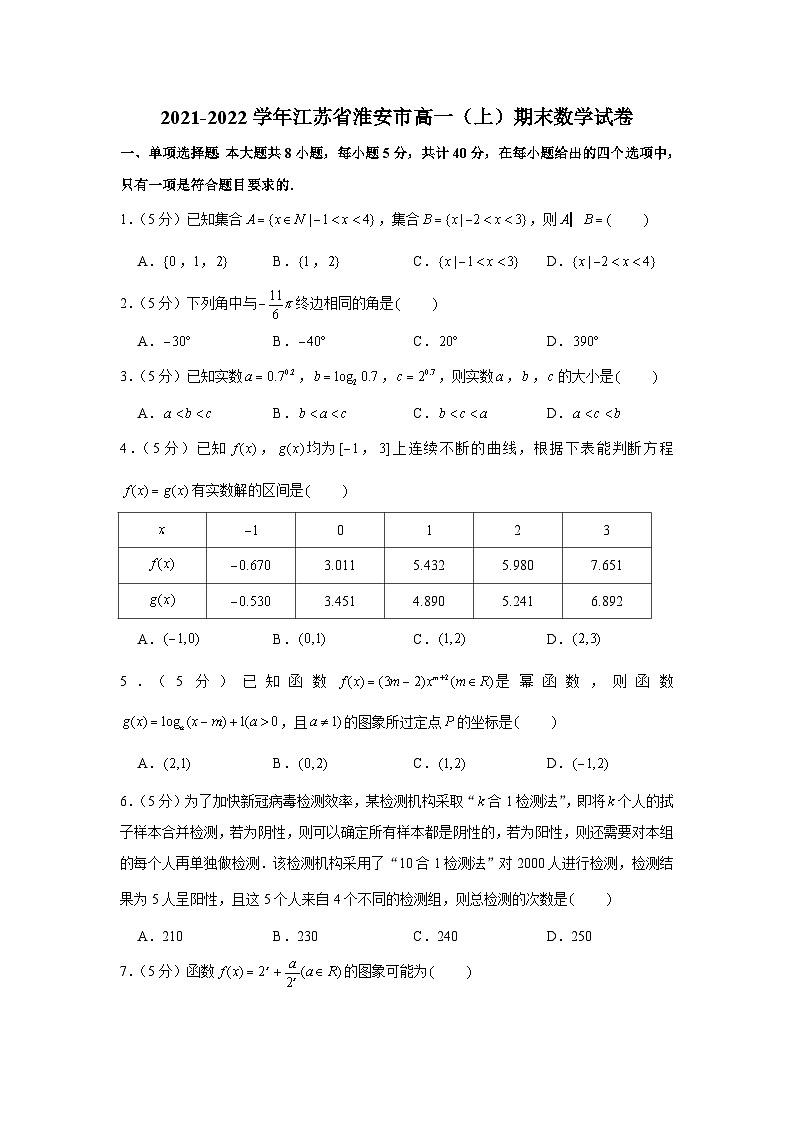
4．（5分）已知，均为，上连续不断的曲线，根据下表能判断方程有实数解的区间是　　

A． B． C． D．

5．（5分）已知函数是幂函数，则函数，且的图象所过定点的坐标是　　

A． B． C． D．

6．（5分）为了加快新冠病毒检测效率，某检测机构采取“合1检测法”，即将个人的拭子样本合并检测，若为阴性，则可以确定所有样本都是阴性的，若为阳性，则还需要对本组的每个人再单独做检测．该检测机构采用了“10合1检测法”对2000人进行检测，检测结果为5人呈阳性，且这5个人来自4个不同的检测组，则总检测的次数是　　

A．210 B．230 C．240 D．250

7．（5分）函数的图象可能为　　

A． B． 

C． D．

8．（5分）已知函数在定义域上是单调增函数，则实数的取值范围为　　

A． B． C． D．

二、多项选择题：本大题共4小题，每小题5分，共计20分．每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．

9．（5分）下列四个函数中，以为最小正周期，且在区间上单调递减的是　　

A． B． C． D．

10．（5分）若，则下列几个不等式中正确的是　　

A． B． 

C． D．

11．（5分）下面选项中正确的有　　

A．命题“所有能被3整除的整数都是奇数”的否定是“存在一个能被3整除的整数不是奇数”             

B．命题“，”的否定是“，” 

C．“，”是“”成立的充要条件 

D．设，，则“”是“”的必要不充分条件

12．（5分）已知函数（其中，，的部分图象如图所示，则下列结论正确的是　　

A．函数是偶函数 

B．函数的图象关于点对称 

C．与图象的所有交点的横坐标之和为 

D．函数的图象可由的图象向右平移个单位得到

三、填空题：本大题共4小题，每题5分，共计20分．

13．（5分）已知函数是定义在上的奇函数，则（2）　　．

14．（5分）数学中处处存在着美，机械学家莱洛沷现的莱洛三角形就给人以对称的美感．莱洛三角形的画法：先画等边三角形，再分别以点，，为圆心，线段长为半径画圆弧，便得到莱洛三角形．若线段长为2，则莱洛三角形的面积是 　　．

15．（5分）已知实数，，且，则的最小值是 　　．

16．（5分）已知定义在上的偶函数，当时，函数，则满足的的取值范围是 　　．

四、解答題：本大题共6小题，共计70分．解答应写出文字说明、证明过程或演算步骤．

17．（10分）设全集是，集合，．

（1）若，求；

（2）问题：已知_____，求实数的取值范围．

从下面给出的三个条件中任选一个，补充在上面的问题中，并进行解答．

①；

②；

③．

18．（12分）（1）计算：；

（2）化简：．

19．（12分）已知函数，．

（1）求函数的定义域；

（2）判断的奇偶性，并证明；

（3）当时，求关于的不等式的解集．

20．（12分）2020年11月22日，习近平在二十国集团领导人利雅得峰会“守护地球”主题会议上指出，根据“十四五”规划和2035年远景目标建议，中国将推动能源清洁低碳安全高效利用，加快新能源、绿色环保等产业发展，促进经济社会发展全面绿色转型．淮安某光伏企业投资144万元用于太阳能发电项目，年内的总维修保养费用为万元，该项目每年可给公司带来100万元的收入．假设到第年底，该项目的纯利润为．（纯利润累计收入总维修保养费一投资成本）

（1）写出的表达式，并求该项目从第几年起开始盈利；

（2）若干年后，该公司为了投资新项目，决定转让该项目，现有以下两种处理方案：

①年平均利润最大时，以72万元转让该项目；

②纯利润最大时，以8万元转让该项目；

你认为以上哪种方案最有利于该公司的发展？并说明理由．

21．（12分）已知函数．

（1）若的最小正周期，求在，上单调递减区间；

（2）若，都有，求的最小值；

（3）若在上仅有一个零点，求的取值范围．

22．（12分）已知函数．

（1）若关于的不等式的解集为，求的零点；

（2）若函数在，的最大值是11，求实数的值；

（3）定义：区间，的长度为．若在任意的长度为1的区间上，存在两点函数值之差的绝对值不小于1，求实数的最小值．

2021-2022学年江苏省淮安市高一（上）期末数学试卷

参考答案与试题解析

一、单项选择题：本大题共8小题，每小题5分，共计40分，在每小题给出的四个选项中，只有一项是符合题目要求的．

1．（5分）已知集合，集合，则　　

A．，1， B．， C． D．

【解答】解：集合，1，2，，集合，

，1，，

故选：．

2．（5分）下列角中与终边相同的角是　　

A． B． C． D．

【解答】解：，

与角终边相同的角的集合为，，

取，得，

与角终边相同的角是．

故选：．

3．（5分）已知实数，，，则实数，，的大小是　　

A． B． C． D．

【解答】解：，，，

．

故选：．

4．（5分）已知，均为，上连续不断的曲线，根据下表能判断方程有实数解的区间是　　

A． B． C． D．

【解答】解：令，

则，（1）（1）（1），

由题意得连续，根据函数的零点判定定理可知，在上有零点，

所以在上有解．

故选：．

5．（5分）已知函数是幂函数，则函数，且的图象所过定点的坐标是　　

A． B． C． D．

【解答】解：函数是幂函数，

，，

，

令得，此时（2），

函数的图象所过定点的坐标是，

故选：．

6．（5分）为了加快新冠病毒检测效率，某检测机构采取“合1检测法”，即将个人的拭子样本合并检测，若为阴性，则可以确定所有样本都是阴性的，若为阳性，则还需要对本组的每个人再单独做检测．该检测机构采用了“10合1检测法”对2000人进行检测，检测结果为5人呈阳性，且这5个人来自4个不同的检测组，则总检测的次数是　　

A．210 B．230 C．240 D．250

【解答】解：根据题意，采用“10合1检测法”对2000人进行检测，

需要先将2000人按每组10人进行分组，需要分200组，即需要检测200次，

结果为5人呈阳性，且这5个人来自4个不同的检测组，需要对这4组进行第二轮检测，需要检测40次，

则一共需要检测次，

故选：．

7．（5分）函数的图象可能为　　

A． B． 

C． D．

【解答】解：当时，，故选项满足；

当时，，且，，此时函数为偶函数，图象关于轴对称，故选项满足；

当时，，，且，此时函数为奇函数，图象关于原点对称，故选项满足；

图象过点，此时，故选项不满足．

故选：．

8．（5分）已知函数在定义域上是单调增函数，则实数的取值范围为　　

A． B． C． D．

【解答】解：函数在定义域上是单调增函数，

，解得，

实数的取值范围为，，

故选：．

二、多项选择题：本大题共4小题，每小题5分，共计20分．每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．

9．（5分）下列四个函数中，以为最小正周期，且在区间上单调递减的是　　

A． B． C． D．

【解答】解：最小正周期为，在区间 上 单调递减；

最小正周期为，在区间 上单调递减；

最小正周期为，在区间 上单调递减；

最小正周期为，在区间 上单调递增；

故选：．

10．（5分）若，则下列几个不等式中正确的是　　

A． B． 

C． D．

【解答】解：对于：当，时，，故错误；

对于，则，故正确；

对于，则，故正确；

对于，则，

则，故正确．

故选：．

11．（5分）下面选项中正确的有　　

A．命题“所有能被3整除的整数都是奇数”的否定是“存在一个能被3整除的整数不是奇数”             

B．命题“，”的否定是“，” 

C．“，”是“”成立的充要条件 

D．设，，则“”是“”的必要不充分条件

【解答】解：对于：命题“所有能被3整除的整数都是奇数”的否定是“存在一个能被3整除的整数不是奇数”，故正确；

对于：命题“，”的否定是“，”，故错误；

对于：当“，”时，“”成立，反之也成立，故“，”是“”成立的充要条件；故正确；

对于：设，，则“，”时，则“”，反之成立，故设，，则“”是“”的必要不充分条件，故正确．

故选：．

12．（5分）已知函数（其中，，的部分图象如图所示，则下列结论正确的是　　

A．函数是偶函数 

B．函数的图象关于点对称 

C．与图象的所有交点的横坐标之和为 

D．函数的图象可由的图象向右平移个单位得到

【解答】解：根据函数（其中，，的部分图象，

可得，，．

结合五点法作图，可得，，，

故，为非奇非偶函数，故错误；

令，求得，故函数的图象关于点对称，故正确；

直线与图象的所有交点的横坐标满足．

由于，故满足的值共计有4个，设它们分别为、、、．

则，，

故交点的横坐标之和为，

故正确；

把函数的图象向右平移个单位得到 的图象，故错误，

故选：．

三、填空题：本大题共4小题，每题5分，共计20分．

13．（5分）已知函数是定义在上的奇函数，则（2）　0　．

【解答】解：函数是定义在上的奇函数，

，，

（2），

故答案为：0．

14．（5分）数学中处处存在着美，机械学家莱洛沷现的莱洛三角形就给人以对称的美感．莱洛三角形的画法：先画等边三角形，再分别以点，，为圆心，线段长为半径画圆弧，便得到莱洛三角形．若线段长为2，则莱洛三角形的面积是 　　．

【解答】解：由已知得，

则，故扇形的面积为，

莱洛三角形的面积扇形面积的3倍减去三角形面积的2倍，

所求面积为．

故答案为：．

15．（5分）已知实数，，且，则的最小值是 　　．

【解答】解：，，且，

，

，

当且仅当，即，时取等号，

的最小值是，

故答案为：．

16．（5分）已知定义在上的偶函数，当时，函数，则满足的的取值范围是 　，　．

【解答】解：当时，函数，

函数在，上单调递减，

不等式可化为，

又函数为定义在上的偶函数，，

不等式可化为，

，

，

，

即满足的的取值范围是，，

故答案为：，．

四、解答題：本大题共6小题，共计70分．解答应写出文字说明、证明过程或演算步骤．

17．（10分）设全集是，集合，．

（1）若，求；

（2）问题：已知_____，求实数的取值范围．

从下面给出的三个条件中任选一个，补充在上面的问题中，并进行解答．

①；

②；

③．

【解答】解：（1）时，或，，

所以，，，；

（2）若选①，则，

所以或，

所以或，

所以的范围为或，

若选②，则，

所以或，

所以或，

所以的范围为或，

若选③，则，即，

所以的范围为，．

18．（12分）（1）计算：；

（2）化简：．

【解答】解：（1）

；

（2）

．

19．（12分）已知函数，．

（1）求函数的定义域；

（2）判断的奇偶性，并证明；

（3）当时，求关于的不等式的解集．

【解答】解：（1）根据题意，函数，

则有，解可得，

即函数的定义域为，；

（2）根据题意，函数为奇函数，

证明如下：函数的定义域为，，关于原点对称，

，

则函数为奇函数，

（3）即，

又由，则函数为减函数，

则有，解可得，

即的解集为，．

20．（12分）2020年11月22日，习近平在二十国集团领导人利雅得峰会“守护地球”主题会议上指出，根据“十四五”规划和2035年远景目标建议，中国将推动能源清洁低碳安全高效利用，加快新能源、绿色环保等产业发展，促进经济社会发展全面绿色转型．淮安某光伏企业投资144万元用于太阳能发电项目，年内的总维修保养费用为万元，该项目每年可给公司带来100万元的收入．假设到第年底，该项目的纯利润为．（纯利润累计收入总维修保养费一投资成本）

（1）写出的表达式，并求该项目从第几年起开始盈利；

（2）若干年后，该公司为了投资新项目，决定转让该项目，现有以下两种处理方案：

①年平均利润最大时，以72万元转让该项目；

②纯利润最大时，以8万元转让该项目；

你认为以上哪种方案最有利于该公司的发展？并说明理由．

【解答】解：（1）由题意可知为正整数），

令得，

解得，

所以从第3年起开始盈利．

（2）若选择方案①，设年平均利润为，

则，当且仅当即时，等号成立，

所以当时，取得最大值32，

此时共盈利为（万元）；

若选择方案②，纯利润，

所以当时，纯利润取得最大值256，

此时共盈利为（万元），

若该公司6年后投资其他项目，确定盈利则选择方案①，

若该公司6年后投资其他项目，确定亏损则选择方案②，

事实上，投资任何一个项目都有风险，并不一定年限少，盈利就多，就更有利于公司的发展．

21．（12分）已知函数．

（1）若的最小正周期，求在，上单调递减区间；

（2）若，都有，求的最小值；

（3）若在上仅有一个零点，求的取值范围．

【解答】解：（1），

，，

；

令，

解得，

又，，

在，上单调递减区间为，；

（2）对，都有，

，

，

解得，

又，

的最小值为；

（3），，，

由题意知，

，

即且，

故，

故，2或3；

分别代入得，，，

故的取值范围为，，，．

22．（12分）已知函数．

（1）若关于的不等式的解集为，求的零点；

（2）若函数在，的最大值是11，求实数的值；

（3）定义：区间，的长度为．若在任意的长度为1的区间上，存在两点函数值之差的绝对值不小于1，求实数的最小值．

【解答】解：（1）由已知可得，的两根是，，

所以，解得，

所以的零点是和．

（2），

当时，由，，知，，

由复合函数的单调性可知在，上单调递增，

所以当时取得最大值，即，因为，解之得；

当时，由，，知，，

由复合函数的单调性可知在，上单调递减，

所以当时取得最大值，即，解之得．

综上，或．

（3）令，由二次函数的对称性，不妨考虑的情形：

①若，只需，

即，解之得；

②若，只需，

又由得，即，，

综上，的最小值为4．

声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2022/8/1 9:03:29；用户：高中数学6；邮箱：tdjyzx38@xyh.com；学号：42412367