




【期末分层模拟】(基础卷·沪科版)2022-2023学年八年级数学下学期期末模拟卷(原卷版+解析版)
展开编者小注:
本套专辑为沪科版地区2022-2023学年第二学期期末考试研发。
7-8年级(满分100分制),分基础卷(适合80分以下学生使用)、提升卷(适合80-95分学生使用)、满分卷(适合95分以上学生使用)。
来源为近两年沪科版数学教材使用地期末原题,包含详细解析。
所有资料研发均为原创,希望助广大中学生一臂之力。
(基础卷)2022-2023学年八年级数学下学期期末考试卷(原卷版)(沪科版)
学校:___________姓名:___________班级:___________考号:___________
一、单选题(共0分
1.某班大课间活动抽查了名学生每分钟跳绳次数,获得如下数据(单位:次):,,,,,,,,,,,,,,,,,,,. 则跳绳次数在这一组的频数所占的百分比是( )
A. B. C.3 D.
2.如图1所示的是被称作“通州八景”之一的燃灯佛舍利塔,它巍峨挺拔,雄伟壮观,始建于北周年间,是北京地区建造年代最早、最高大的佛塔之一.燃灯佛舍利塔为八角形十三层砖木结构密檐式塔,十三层均为正八边形砖木结构,图2所示的正八边形是其中一层的平面示意图,其内角和为( )
A. B. C. D.
3.为执行“均衡教育”政策,某区年投入教育经费 万元,预计到 年底三年累计投入 亿元,若每年投入教育经费的年平均增长百分率为 ,则下列方程正确的是( )
A.
B.
C.
D.
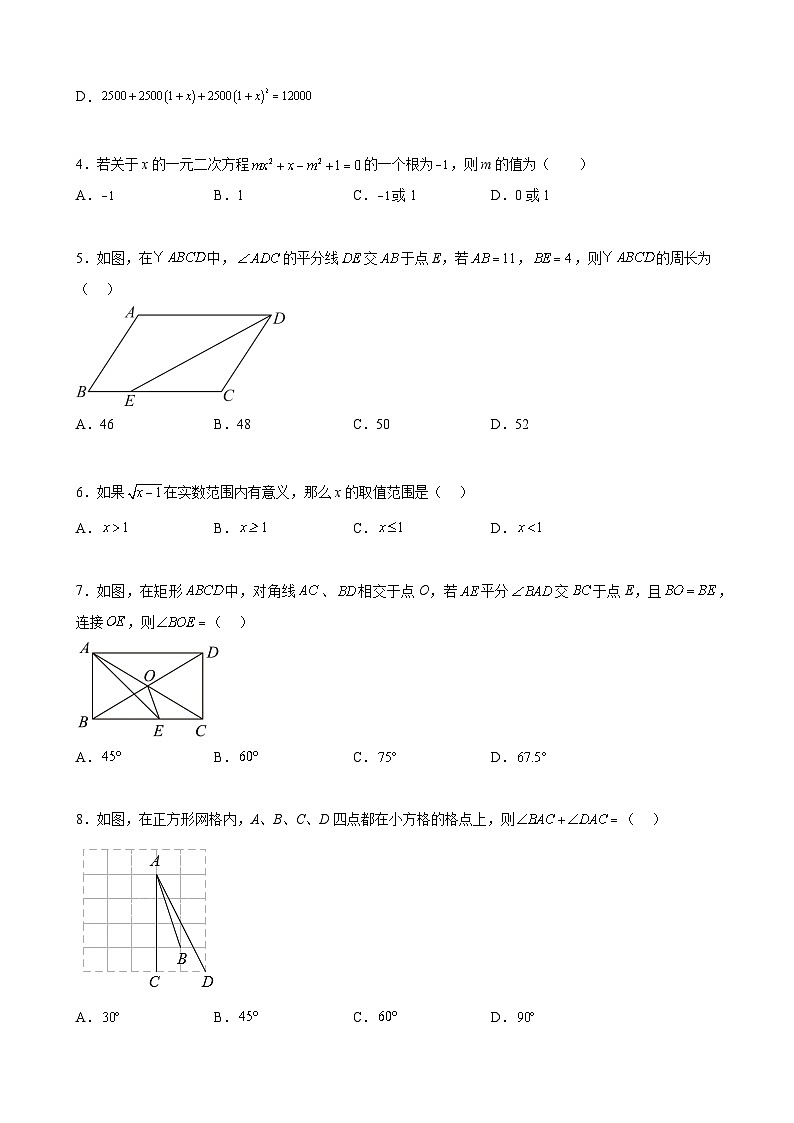
4.若关于x的一元二次方程的一个根为,则m的值为( )
A. B.1 C.或1 D.0或1
5.如图,在中,的平分线交于点E,若,,则的周长为( )
A.46 B.48 C.50 D.52
6.如果在实数范围内有意义,那么x的取值范围是( )
A. B. C. D.
7.如图,在矩形中,对角线、相交于点O,若平分交于点E,且,连接,则( )
A. B. C. D.
8.如图,在正方形网格内,A、B、C、D四点都在小方格的格点上,则( )
A. B. C. D.
9.在平面直角坐标系中,点到原点的距离是( )
A.3 B.4 C.5 D.
10.若,则 化简后的结果是( )
A.xy B. C. D.
二、填空题(共0分
11.如图的四边形是某地板厂加工地板时剩下的边角余料,如果用这种相同的四边形木板进行镶嵌,则至少需要___________块才能完成镶嵌.
12.如图,在四边形ABCD中,ADBC且AD=9cm,BC=7cm,点P、Q分别从点A、C同时出发,点P以1cm/s的速度由A向D运动,点Q以2cm/s的速度由C向B运动,Q运动到B处停止运动,_____秒后直线PQ将四边形ABCD截出一个平行四边形.
13.如图,中俄“海上联合﹣2017”军事演习在海上编队演习中,两艘航母护卫舰从同一港口同时出发,一号舰沿南偏西方向以12海里/小时的速度航行,二号舰以16海里/小时速度航行,离开港口1.5小时后它们分别到达,两点,相距30海里,则二号舰航行的方向是_________.
14.有一组勾股数,知道其中的两个数分别是24和7,则第三个数是_____.
15.对于代数式(,a,b,c为常数)①若,则有两个相等的实数根;②存在三个实数,使得;③若与方程的解相同,则,以上说法正确的是___________.
16.最简二次根式与可以合并,则a的值为 _____.
17.在实数范围内,若有意义,则x的取值范围是______.
18.关于x的一元二次方程的两个实数根分别为2和,则因式分解的结果是__________.
三、解答题(共0分
19.化简求值
(1)已知,,试求代数式的值.
(2)先化简,再求值,其中,.
20.甲、乙两船同时从港口出发,甲船以6海里/时的速度向北偏东航行,乙船向南偏东航行.2小时后,甲船到达岛,乙船到达岛,若、两地相距20海里,问乙船的速度是每小时多少海里?
21.(1)一个多边形的内角和是外角和的3倍,这个多边形是几边形?
(2)小明求得一个多边形的内角和为,小强很快发现小明所得的度数有误,后来小明复查时发现他重复加了一个内角,求出这个多边形的边数以及他重复加的那个角的度数.
22.【问题情境】数学活动课上,老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动.
【实践发现】同学们随机收集芒果树、荔枝树的树叶各10片,通过测量得到这些树叶的长y
(单位:cm),宽x(单位:cm)的数据后,分别计算长宽比,整理数据如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
芒果树叶的长宽比 | 3.8 | 3.7 | 3.5 | 3.4 | 3.8 | 4.0 | 3.6 | 4.0 | 3.6 | 4.0 |
荔枝树叶的长宽比 | 2.0 | 2.0 | 2.0 | 2.4 | 1.8 | 1.9 | 1.8 | 2.0 | 1.3 | 1.9 |
【实践探究】分析数据如下:
| 平均数 | 中位数 | 众数 | 方差 |
芒果树叶的长宽比 | 3.74 | m | 4.0 | 0.0424 |
荔枝树叶的长宽比 |
| 1.95 | n | 0.0669 |
【问题解决】
(1)m= ,n= ,求荔枝树叶的长宽比的平均数.
(2)A同学说:“从树叶的长宽比的方差来看,我认为芒果树叶的形状差别大.”B同学说:“从树叶的长宽比的平均数、中位数和众数来看,我发现荔枝树叶的长约为宽的两倍.” 以上两位同学的说法中,合理的是 同学;
(3)现有一片长,宽的树叶,请判断这片树叶更可能来自于芒果、荔枝中的哪种树?并给出你的理由.
23.某汽车销售公司计划4月份销售A,B两种型号的汽车共10辆,A,B两种型号汽车的进价和售价如下表:
| A | B |
进价(万元/辆) | 10 | 12 |
售价(万元/辆) | 13 | 15 |
供货商和汽车销售公司商定:若当月A型汽车销售量超过5辆,则每多售出1辆,所有售出的A型汽车进价均降低万元/辆,B型汽车也是如此.若汽车销售公司当月正好完成A,B两种型号汽车的销售计划,设当月A型汽车销售量为x辆.
(1)设当月A型汽车实际进价为y万元/辆,求y与x的函数表达式.
(2)若当月销售利润为万元,则当月需售出A型汽车多少辆?
24.如图,在菱形中,,点,将对角线三等分,且,连接,,,.
(1)求证:四边形是菱形.
(2)求菱形的面积.
【期末分层模拟】(基础卷·苏科版)2022-2023学年八年级数学下学期期末模拟卷(原卷版+解析版): 这是一份【期末分层模拟】(基础卷·苏科版)2022-2023学年八年级数学下学期期末模拟卷(原卷版+解析版),文件包含基础卷期末考试卷解析版苏科版docx、基础卷期末考试卷原卷版苏科版docx等2份试卷配套教学资源,其中试卷共25页, 欢迎下载使用。
【期末分层模拟】(基础卷·浙教版)2022-2023学年八年级数学下学期期末模拟卷(原卷版+解析版): 这是一份【期末分层模拟】(基础卷·浙教版)2022-2023学年八年级数学下学期期末模拟卷(原卷版+解析版),文件包含基础卷期末考试卷解析版浙教版docx、基础卷期末考试卷原卷版浙教版docx等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。
【期末分层模拟】(满分卷·沪科版)2022-2023学年八年级数学下学期期末模拟卷(原卷版+解析版): 这是一份【期末分层模拟】(满分卷·沪科版)2022-2023学年八年级数学下学期期末模拟卷(原卷版+解析版),文件包含满分卷期末考试卷解析版沪科版docx、满分卷期末考试卷原卷版沪科版docx等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。












