河北省衡水中学2017届高三押题卷（II卷）文数试题

2017年普通高等学校招生全国统一考试模拟试题

文科数学（Ⅱ）

第Ⅰ卷（共60分）

一、选择题：本大题共12个小题,每小题5分,共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．

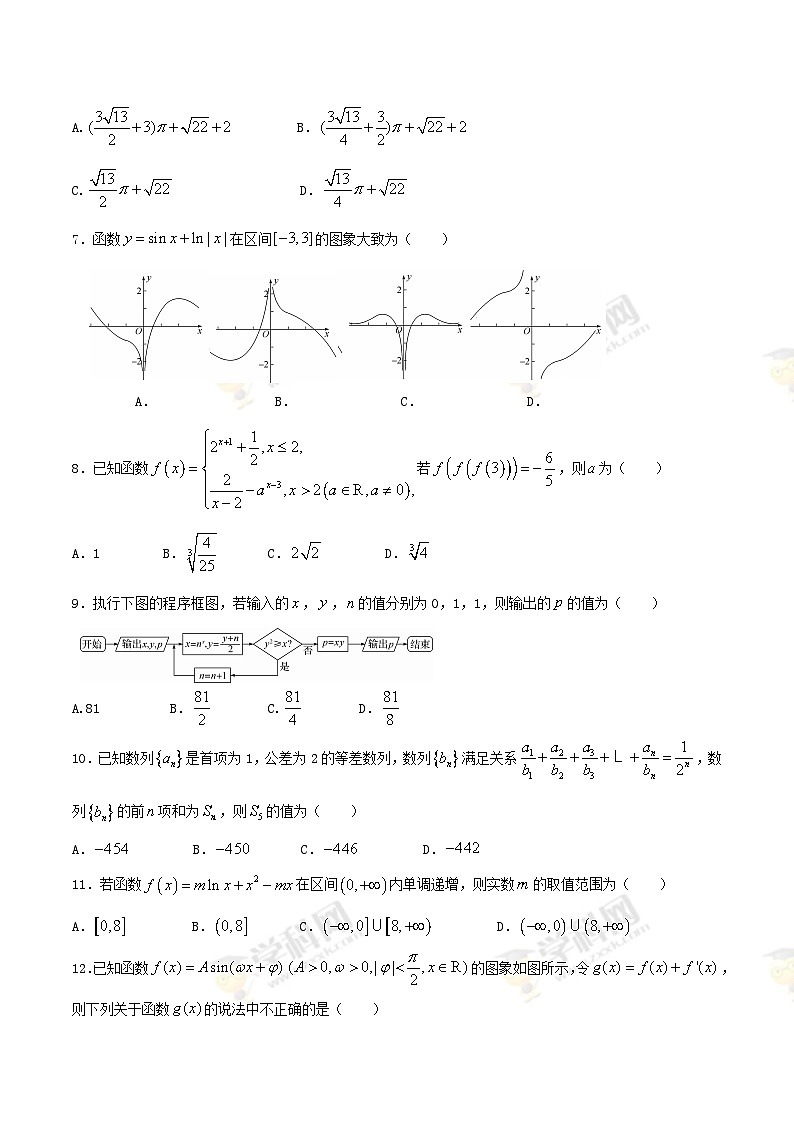
1．设集合，，则集合为（    ）

A．         B．       C．       D．

2．若复数（，）满足，则的值为（    ）

A．          B．       C．      D．

3．若，，则的值为（    ）

A.             B．             C.           D．

4．抛掷一枚质地均匀的骰子两次，记事件两次的点数均为偶数且点数之差的绝对值为2，则（    ）

A．         B．       C．         D．

5．定义平面上两条相交直线的夹角为：两条相交直线交成的不超过的正角.已知双曲线：，当其离心率时，对应双曲线的渐近线的夹角的取值范围为（    ）

A．               B．                C.               D．

6.某几何体的三视图如图所示，若该几何体的体积为，则它的表面积是（    ）

A.         B．

C.                  D．

7．函数在区间的图象大致为（    ）

         A．                 B．               C．               D．

8．已知函数若，则为（    ）

A．1         B．       C．         D．

9．执行下图的程序框图，若输入的，，的值分别为0，1，1，则输出的的值为（    ）

A.81          B．        C.        D．

10．已知数列是首项为1，公差为2的等差数列，数列满足关系，数列的前项和为，则的值为（    ）

A．         B．       C．         D．

11．若函数在区间内单调递增，则实数的取值范围为（    ）

A．         B．       C．         D．

12．已知函数的图象如图所示，令，则下列关于函数的说法中不正确的是（    ）

A. 函数图象的对称轴方程为

B．函数的最大值为      

C. 函数的图象上存在点，使得在点处的切线与直线平行

D．方程的两个不同的解分别为，，则的最小值为

第Ⅱ卷（共90分）

二、填空题（每题5分，满分20分，将答案填在答题纸上）

13．向量，，若向量，共线，且，则的值为          ．

14．已知点，，若圆上存在点使，则的最小值为          ．

15．设，满足约束条件则的最大值为          ．

16．在平面五边形中，已知，，，，，，当五边形的面积时，则的取值范围为          ．

三、解答题 （本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）

17．在中，角，，所对的边分别为，，，且.

（1）求角；

（2）若，的面积为，为的中点，求的长.

18．如图所示的几何体中，四边形为菱形，，，，，平面平面，，为的中点，为平面内任一点.

（1）在平面内，过点是否存在直线使？如果不存在，请说明理由，如果存在，请说明作法；

（2）过，，三点的平面将几何体截去三棱锥，求剩余几何体的体积.

19．某校为缓解高三学生的高考压力，经常举行一些心理素质综合能力训练活动，经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试，并将其成绩分为、、、、五个等级，统计数据如图所示（视频率为概率），根据图中抽样调查的数据，回答下列问题：

（1）试估算该校高三年级学生获得成绩为的人数；

（2）若等级、、、、分别对应100分、90分、80分、70分、60分，学校要求当学生获得的等级成绩的平均分大于90分时，高三学生的考前心理稳定，整体过关，请问该校高三年级目前学生的考前心理稳定情况是否整体过关？

（3）以每个学生的心理都培养成为健康状态为目标，学校决定对成绩等级为的16名学生（其中男生4人，女生12人）进行特殊的一对一帮扶培训，从按分层抽样抽取的4人中任意抽取2名，求恰好抽到1名男生的概率..

20．已知椭圆：的离心率为，且过点，动直线：交椭圆于不同的两点，，且（为坐标原点）

（1）求椭圆的方程.

（2）讨论是否为定值.若为定值，求出该定值，若不是，请说明理由.

21．设函数.

（1）试讨论函数的单调性；

（2）如果且关于的方程有两解，（），证明.

请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．

22．选修4-4：坐标系与参数方程

在直角坐标系中，曲线：（为参数，），在以坐标原点为极点，轴的非负半轴为极轴的极坐标系中，曲线：.

（1）试将曲线与化为直角坐标系中的普通方程，并指出两曲线有公共点时的取值范围；

（2）当时，两曲线相交于，两点，求的值.

23．选修4-5：不等式选讲

已知函数.

（1）在给出的直角坐标系中作出函数的图象，并从图中找出满足不等式的解集；

（2）若函数的最小值记为，设，且有，试证明：.

试卷答案

一、选择题

1-5:BCAAD       6-10:AADCB      11、12：AC

二、填空题

13．          14．16           15．           16．

三、解答题

17．解：（1）由，

得.

由正弦定理，得，

即.

又由余弦定理，得.

因为，所以.

（2）因为，

所以为等腰三角形，且顶角.

故，所以.

在中，由余弦定理，得

.

解得.

18．解：（1）过点存在直线使，理由如下：

由题可知为的中点，又为的中点，

所以在中，有.

若点在直线上，则直线即为所求作直线，

所以有；

若点不在直线上，在平面内，

过点作直线，使，

又，所以，

即过点存在直线使.

（2）连接，，则平面将几何体分成两部分：

三棱锥与几何体（如图所示）.

因为平面平面，且交线为，

又，所以平面.

故为几何体的高.

又四边形为菱形，，，，

所以，

所以.

又，所以平面，

所以，

所以几何体的体积.

19．解：（1）从条形图中可知这100人中，有56名学生成绩等级为，

故可以估计该校学生获得成绩等级为的概率为，

则该校高三年级学生获得成绩等级为的人数约有.

（2）这100名学生成绩的平均分为（分），

因为，所以该校高三年级目前学生的“考前心理稳定整体”已过关.

（3）按分层抽样抽取的4人中有1名男生，3名女生，记男生为，3名女生分别为，，.从中抽取2人的所有情况为，，，，，，共6种情况，其中恰好抽到1名男生的有，，，共3种情况，故所求概率.

20．解：（1）由题意可知，

所以，整理，得，①

又点在椭圆上，所以有，②

由①②联立，解得，，

故所求的椭圆方程为.

（2）为定值，理由如下：

设，由，

可知.

联立方程组

消去，化简得，

由，

得，

由根与系数的关系，得

，，③

由，，

得，

整理，得.

将③代入上式，得.

化简整理，得，即.

21．解：（1）由，可知.

因为函数的定义域为，所以，

①若，则当时，，函数单调递减，当时，，函数单调递增；

②若，则当在内恒成立，函数单调递增；

③若，则当时，，函数单调递减，当时，，函数单调递增.

（2）要证，只需证.

设，

因为，

所以为单调递增函数.

所以只需证，

即证，

只需证.（*）

又，，

所以两式相减，并整理，得.

把代入（*）式，

得只需证，

可化为.

令，得只需证.

令（），

则，

所以在其定义域上为增函数，

所以.

综上得原不等式成立.

22．解：（1）曲线：消去参数可得普通方程为.

由，得.故曲线：化为平面直角坐标系中的普通方程为.

当两曲线有公共点时的取值范围为.

（2）当时，曲线：即，

联立方程消去，得两曲线的交点，所在直线方程为.

曲线的圆心到直线的距离为，

所以.

23. 解：（1）因为

所以作出函数的图象如图所示.

从图中可知满足不等式的解集为.

（2）证明：从图中可知函数的最小值为，即.

所以，从而，

故.

当且仅当时，等号成立，

即，时，原式有最小值，

所以得证.