中考数学三轮冲刺《三角形》解答题冲刺练习11（含答案）

中考数学三轮冲刺《三角形》

解答题冲刺练习11

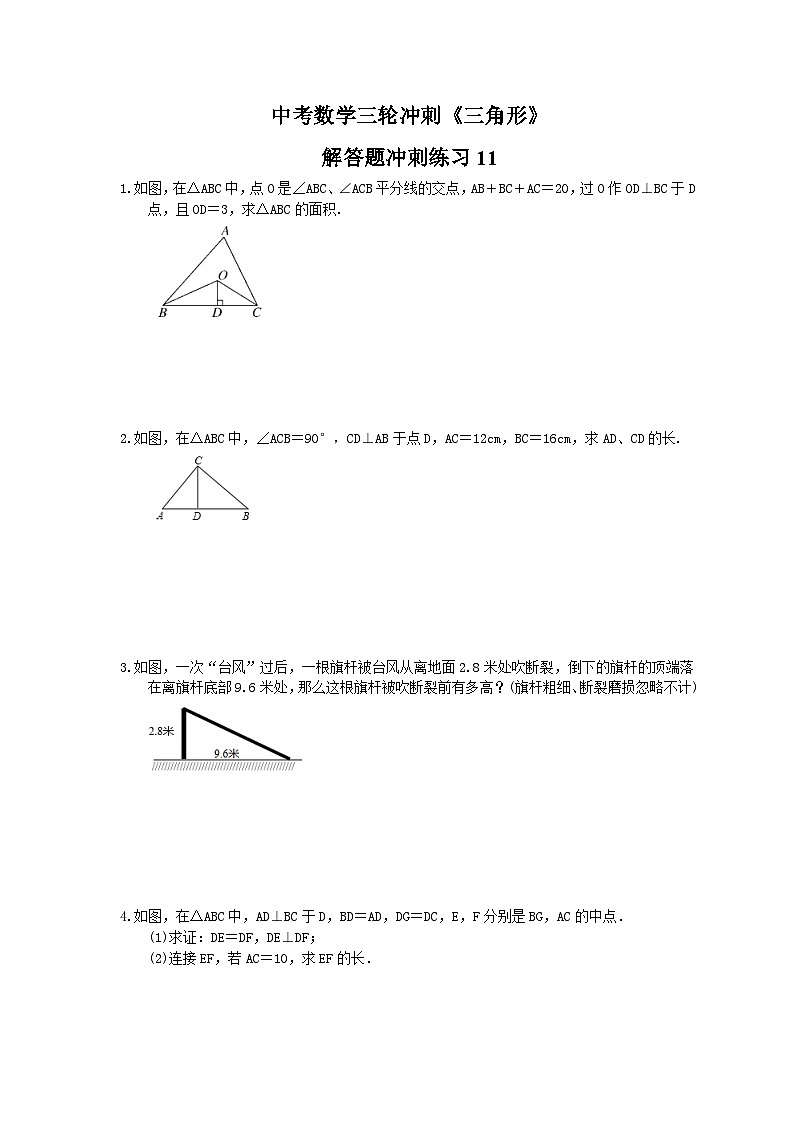
1.如图，在△ABC中，点O是∠ABC、∠ACB平分线的交点，AB＋BC＋AC＝20，过O作OD⊥BC于D点，且OD＝3，求△ABC的面积.

2.如图，在△ABC中，∠ACB＝90°，CD⊥AB于点D，AC＝12cm，BC＝16cm，求AD、CD的长.

3.如图，一次“台风”过后，一根旗杆被台风从离地面2.8米处吹断裂，倒下的旗杆的顶端落在离旗杆底部9.6米处，那么这根旗杆被吹断裂前有多高？(旗杆粗细、断裂磨损忽略不计)

4.如图，在△ABC中，AD⊥BC于D，BD＝AD，DG＝DC，E，F分别是BG，AC的中点．

(1)求证：DE＝DF，DE⊥DF；

(2)连接EF，若AC＝10，求EF的长．

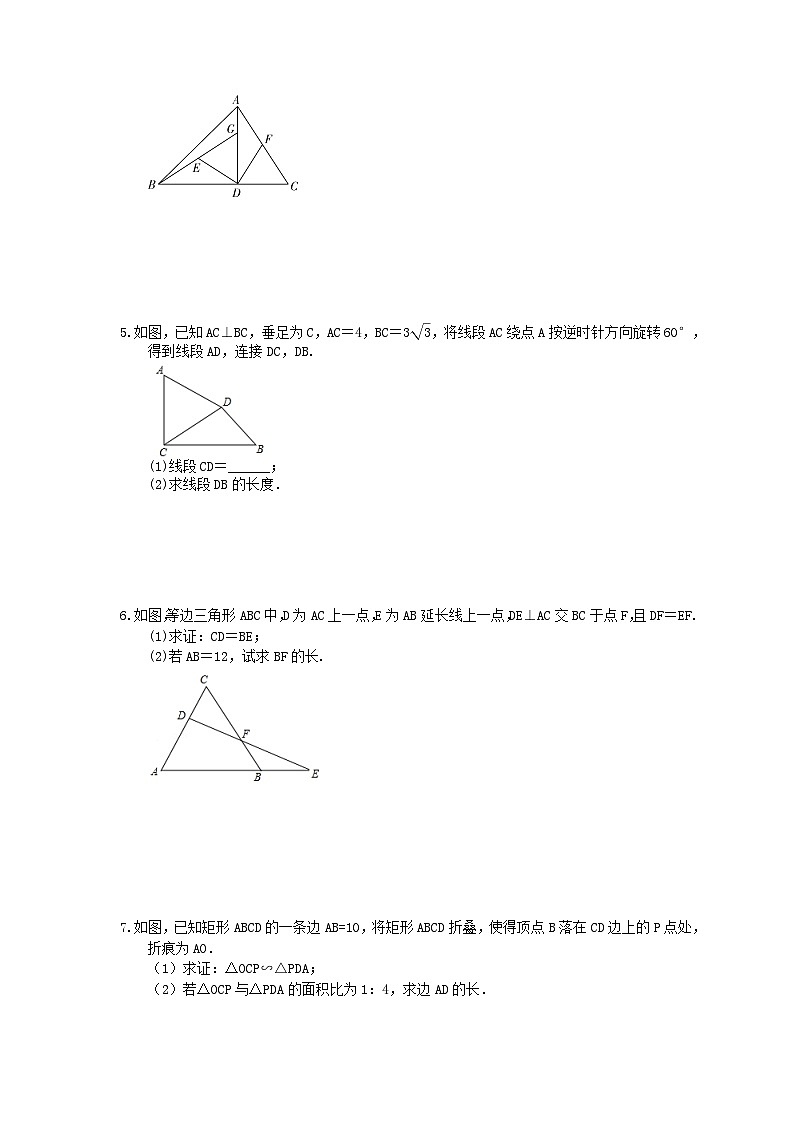
5.如图，已知AC⊥BC，垂足为C，AC＝4，BC＝3，将线段AC绕点A按逆时针方向旋转60°，得到线段AD，连接DC，DB.

(1)线段CD＝______；

(2)求线段DB的长度．

6.如图，等边三角形ABC中，D为AC上一点，E为AB延长线上一点，DE⊥AC交BC于点F，且DF＝EF.

(1)求证：CD＝BE；

(2)若AB＝12，试求BF的长.

7.如图，已知矩形ABCD的一条边AB=10，将矩形ABCD折叠，使得顶点B落在CD边上的P点处，折痕为AO．

（1）求证：△OCP∽△PDA；

（2）若△OCP与△PDA的面积比为1：4，求边AD的长．

8.如图，在矩形ABCD中，AC是对角线，E是AC的中点，过E作MN交AD于M，交BC于N.

⑴求证：AM=CN；⑵若∠CEN=90°，EN:AB=2:3，EC=3，求BC的长.

9.如图,在矩形ABCD中,AE平分∠BAD,交BC于E，过E做EF⊥AD于F,连接BF交AE于P,连接PD．

（1）求证：四边形ABEF是正方形；

（2）如果AB=4，AD=7，求tan∠ADP的值．

10.如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连接CD,DE．

（1）求证：DE是⊙O的切线；

（2）若BD=4，CD=3，求AC的长．

11.如图，已知Rt△ABC，∠ACB=90°，tan∠BAC=2，O在BC上一点，以OC为半径作⊙O，且AO平分∠BAC.

 （1）求证：AB为⊙O切线；

 （2）若⊙O的半径为4，求AC的长.

12.如图，已知AB是⊙O的直径，点C在⊙O上，CD是⊙O的切线，AD⊥CD于点D，E是AB延长线上一点，CE交⊙O于点F，连结OC，AC.

(1)求证：AC平分∠DAO.

(2)若∠DAO=105°，∠E=30°.

①求∠OCE的度数；

②若⊙O的半径为2 ，求线段EF的长.

0.中考数学三轮冲刺《三角形》解答题冲刺练习11（含答案）答案解析

一         、解答题

1.解：如图，过点O作OE⊥AB于E，OF⊥AC于F，连接OA.

∵点O是∠ABC，∠ACB平分线的交点，

∴OE＝OD，OF＝OD，即OE＝OF＝OD＝3，

∴S△ABC＝S△ABO＋S△BCO＋S△ACO＝AB•OE＋BC•OD＋AC•OF

＝×2×(AB＋BC＋AC)＝×3×20＝30.

2.解：∵∠ACB＝90°AC＝12cm，BC＝16cm，

∴AB＝20cm.

根据直角三角形的面积公式，得CD＝9.6cm.

在Rt△ACD中，AD＝7.2cm.

3.解：∵旗杆剩余部分、折断部分与地面正好构成直角三角形，

∴BC＝＝＝10m，

∴旗杆的高＝AB＋BC＝2.8＋10＝12.8m.

答：这根旗杆被吹断裂前有12.8米高.

4.证明：(1)∵AD⊥BC，

∴∠ADB＝∠ADC＝90°，

在△BDG和△ADC中，

，

∴△BDG≌△ADC(SAS)，

∴BG＝AC，∠BGD＝∠C，

∵∠ADB＝∠ADC＝90°，E，F分别是BG，AC的中点，

∴DE＝BG＝EG，DF＝AC＝AF，

∴DE＝DF，∠EDG＝∠EGD，∠FDA＝∠FAD，

∴∠EDG＋∠FDA＝90°，

∴DE⊥DF；

(2)解：∵AC＝10，

∴DE＝DF＝5，

由勾股定理得，EF＝＝5.

5.解：(1)4；(2)作DE⊥BC于点E.

∵△ACD是等边三角形，

∴∠ACD＝60°，

又∵AC⊥BC，

∴∠DCE＝∠ACB－∠ACD＝90°－60°＝30°，

∴Rt△CDE中，DE＝DC＝2，

CE＝4×＝2，

∴BE＝BC－CE＝3－2＝.

∴Rt△BDE中，BD＝＝＝.　

6.证明：(1)如图，作DM∥AB，交CF于M，则∠DMF＝∠E，

∵△ABC是等边三角形，

∴∠C＝60°＝∠CDM＝∠CMD，

∴△CDM是等边三角形，

∴CD＝DM，

在△DMF和△EBF中，

，

∴△DMF≌△EBF(ASA)，

∴DM＝BE，

∴CD＝BE；

(2)∵ED⊥AC，∠A＝60°＝∠ABC，

∴∠E＝∠BFE＝∠DFM＝∠FDM＝30°，

∴BE＝BF，DM＝FM，

又∵△DMF≌△EBF，

∴MF＝BF，

∴CM＝MF＝BF，

又∵AB＝BC＝12，

∴CM＝MF＝BF＝4.

7.（1）证明：∵四边形ABCD是矩形，∴AD=BC，DC=AB，∠DAB=∠B=∠C=∠D=90°，

由折叠可得：AP=AB，PO=BO，∠PAO=∠BAO，∠APO=∠B，∴∠APO=90°，

∴∠APD=90°﹣∠CPO=∠POC，∵∠D=∠C，∠APD=∠POC，∴△OCP∽△PDA．

（2）解：∵△OCP与△PDA的面积比为1：4，∴==，

∴DA=2CP．设PC=x，则AD=2x，PD=10﹣x，AP=AB=10，

在Rt△PDA中，∵∠D=90°，PD2+AD2=AP2，∴（10﹣x）2+（2x）2=102，

解得：x=4，∴AD=2x=8．

8.略

9.（1）证明：∵四边形ABCDABCD是矩形，

∴∠FAB=∠ABE=90°，AF∥BE，

∵EF⊥AD，

∴∠FAB=∠ABE=∠AFE=90°，

∴四边形ABEF是矩形，

∵AE平分∠BAD，AF∥BE，

∴∠FAE=∠BAE=∠AEB，

∴AB=BE，

∴四边形ABEF是正方形；

（2）解：过点P作PH⊥AD于H，如图所示：

∵四边形ABEF是正方形，

∴BP=PF，BA⊥AD，∠PAF=45°，

∴AB∥PH，

∵AB=4，∴AH=PH=2，

∵AD=7，∴DH=AD﹣AH=7﹣2=5，

在Rt△PHD中，∠PHD=90°．∴tan∠ADP==．

10.解：（1）连接OD，∵BC是⊙O的直径，∴∠BDC=90°，∴∠ADC=90°，

∵E为AC的中点，∴DE=EC=0.5AC，∴∠1=∠2，∵OD=OC，∴∠3=∠4，

∵AC切⊙O于点C，∴AC⊥OC，∴∠1+∠3=∠2+∠4=90°，∴DE⊥OD，∴DE是⊙O的切线；

（2）在Rt△BCD中，∵BD=4，CD=3，∴BC=5，

∵∠BCD=∠BCA=90°，∠B=∠B，∴△BCD∽△BAC，

∴CD:AC=BD:BBC,即3:AC=4:5，∴AC=3.757．

11.略

12.解：(1)证明：∵CD是⊙O的切线，∴OC⊥CD.

又∵AD⊥CD，

∴OC∥AD，∴∠DAC=∠ACO.

∵OA=OC，∴∠OAC=∠ACO，

∴∠DAC=∠OAC，

∴AC平分∠DAO.

(2)①∵OC∥AD，∴∠EOC=∠DAO=105°，

∴∠OCE=180°－∠EOC－∠E=180°－105°－30°=45°.

②如图，过点O作OG⊥CE于点G，

∴FG=CG.

在Rt△OGC中，OC=2 ，∠OCE=45°，

∴OG=CG=OCsin45°=2 ×=2，

∴FG=CG=2.

在Rt△OGE中，OG=2，∠E=30°，

∴EG===2 ，

∴EF=EG－FG=2 －2.