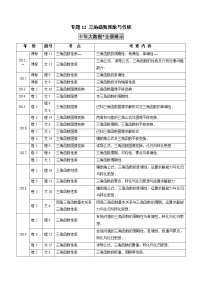
2011-2020年高考数学真题分专题训练 专题12 三角函数图象与性质（教师版含解析）

这是一份2011-2020年高考数学真题分专题训练 专题12 三角函数图象与性质（教师版含解析），共24页。试卷主要包含了已知函数 f x sinx，若 x1  ， x2 ，函数 f ，函数  等内容，欢迎下载使用。

专题 12
三角函数图象与性质
十年大数据*全景展示
年 份
题号
考 点
考 查 内 容
课标
理 11 三角函数性质
文 11 三角函数性质
三角函数的周期性、奇偶性、单调性
2011
三角公式、诱导公式、三角函数的性质及分析处理问题
能力．
课标
课标
课标
卷 2
卷 1
理 9
文 9
三角函数性质
三角函数性质
三角函数的单调性
2012
三角函数的对称轴等性质
三角函数图像平移变换
2013
2014
文 16 三角函数图像变换
文 7
理 8
文 8
三角函数图像
本三角函数的周期性．
2015
卷 1
三角函数图像
已知三角函数图像求解析式及三角函数的单调性．
卷 3
卷 1
卷 2
卷 3
卷 1
理 14 三角函数图像变换
两角和与差的三角公式及图像平移变换．
三角函数周期、三角函数的平移变换．
已知三角函数图像求解析式
文 6
文 3
三角函数图像变换
三角函数图像
2016
文 14 三角函数图像
辅助角公式及三角函数平移变换．
诱导公式、三角函数图像变换，化归与转化思想
三角函数周期、对称性、零点与单调性．
三角函数周期性
理 9
理 6
文 3
三角函数图像变换
2017 卷 3
卷 2
三角函数性质
三角函数性质


辅助角公式、三角函数的单调性，运算求解能力与化归
与转化思想．
卷 2
卷 3
卷 2
理 10 三角函数性质
理 15 三角函数性质
文 10 三角函数性质
三角函数的零点、转化与化归思想与运算求解能力
辅助角公式、三角函数的单调性，运算求解能力与化归
与转化思想．
2018
同角三角函数基本关系 同角三角函数基本关系与三角函数的周期，运算求解能
卷 3
卷 2
文 6
理 9
三角函数性质
力与化归与转化思想．
含绝对值的三角函数的周期性与单调性，转化与化归思
想．
三角函数性质
含绝对值的三角函数的周期性、单调性、极值与零点，
转化与化归思想．
2019 卷 3
理 12 三角函数性质
文 15 三角函数性质
卷 1
卷 2
诱导公式、三角函数的最值，转化与化归思想．
三角函数的极值、周期等性质．
文 8
理 7
文 7
三角函数性质
三角函数图象及其性质 三角函数的图象，三角函数的周期性
三角函数图象及其性质 三角函数的图象，三角函数的周期性
卷 1
2020
理 16 三角函数图象及其性质 三角函数最值，三角函数图象的对称性
文 12 三角函数图象及其性质 三角函数最值，三角函数图象的对称性
卷 3
大数据分析*预测高考
考 点
出现频率
2021 年预测
三角函数性质
三角函数图像
14/21
7/21
2021 年高考仍将重点考查三角函数的图像与性质及三
角函数变换，特别是这些知识点的组合考查是考查的
热点，题型仍为选择题或填空题，难度可以为基础题
或中档题，也可以是压轴题．
三角函数图像变换 4/21
十年试题分类*探求规律
考点 39 三角函数性质
1
( ) =
+
1．(2020 全国Ⅲ文 12 理 16)已知函数 f x sinx
，则 (
)
sinx
( )
( )
B． f x 的图像关于 y轴对称
A． f x 的最小值为2
p
( )
= p对称
D． f x 的图像关于直线
x =
( )
C． f x 的图像关于直线 x
对称
2
【答案】D


【思路导引】根据基本不等式使用条件可判断 A；根据奇偶性可判断 B；根据对称性判断 C，D．
1
【解析】
Qsin x可以为负，所以
A
Q
错；
sin x 0, x k k
¹ \ ¹ p ( ÎZ) Q (- )= -
sin x -
, f
x
= - ( )
f x
，
sin x
1
1
\ ( )关于原点对称；Q f (2p - x) = -sin x -
f x
¹ f (x), f (p - x) = sin x +
= f (x),故 B 错；
sin x
sin x
p
\ f (x)关于直线 x
=
对称，故 C 错，D 对，故选 D．
2
p
p
p
2．(2019•新课标Ⅱ，理 9)下列函数中，以 为周期且在区间( ， ) 单调递增的是(
)
2
4
2
A． f (x) =| cos2x |
B． f (x) =| sin 2x |
C． f (x) = cos | x |
D． f (x) =sin | x |
【答案】A
【解析】 f (x) =sin | x| 不是周期函数，可排除 D 选项； f (x) = cos | x| 的周期为 2p ，可排除 C 选项；
p
p
p
f (x) =| sin 2x| 在 处取得最大值，不可能在区间( ， ) 单调递增，可排除 B ．
4
4
2
故选 A ．
p
3．(2019•新课标Ⅲ，理 12)设函数 f (x) = sin(wx + )(w > 0) ，已知 f (x) 在[0 ，2p]有且仅有 5 个零点．下
5
述四个结论：
① f (x) 在(0, 2p) 有且仅有 3 个极大值点
② f (x) 在(0, 2p) 有且仅有 2 个极小值点
p
③ f (x) 在(0, ) 单调递增
10
12
5
29
10
④w 的取值范围是[
，
)
其中所有正确结论的编号是(
)
A．①④
B．②③
C．①②③
D．①③④
【答案】D
p
p
p
【解析】当 xÎ[0，2p]时，wx + Î[ ，2pw + ]，Q f (x)在[0 ，2p]有且仅有 5 个零点，
5
5
5
p
12
29
10
\5p„2pw + < 6p ，\ „w
0，0 0，∴w =
．
min
4
6
3
p
p
p
23．(2018 江苏)已知函数 y = sin(2x+j)(-