沪科版八年级下册19.3 矩形 菱形 正方形说课ppt课件

这是一份沪科版八年级下册19.3 矩形 菱形 正方形说课ppt课件，共38页。PPT课件主要包含了逐点学练，本节小结，作业提升，学习目标，本节要点，学习流程，感悟新知，知识点，矩形的定义及其性质，矩形的判定等内容，欢迎下载使用。
矩形的定义及其性质直角三角形斜边上的中线的性质矩形的判定
1.定义 有一个角是直角的平行四边形叫做矩形 .
特别提醒1.矩形必须具备两个条件：(1) 它是一个平行四边形；(2) 它有一个角是直角 . 这两个条件缺一不可 .2. 由矩形的定义知，矩形一定是平行四边形，但平行四边形不一定是矩形.矩形的定义可以作为判定一个四边形是矩形的一种方法 .
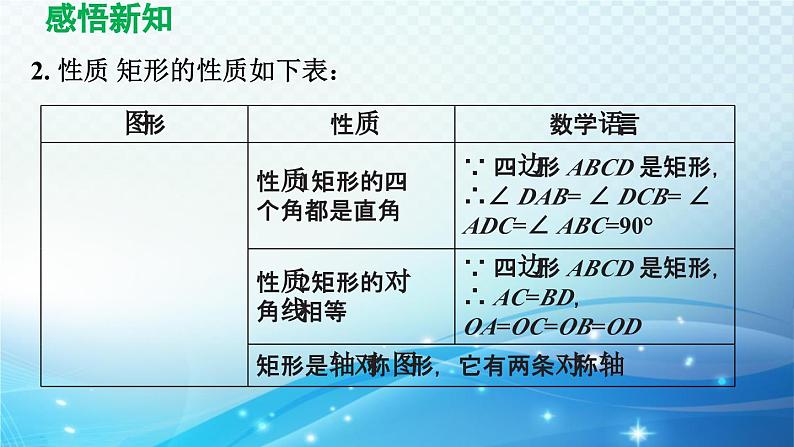
2. 性质 矩形的性质如下表：
特别提醒： 1. 利用矩形的性质可以证明线段相等或存在倍分关系、直线平行、角相等等 .2.矩形的一条对角线把矩形分成两个全等的直角三角形，矩形的两条对角线将矩形分成两对全等的等腰三角形，分成四个面积相等的等腰三角形，因此有关矩形的计算问题经常转化到直角三角形和等腰三角形中来解决 .
[ 中考·遂宁 ] 如图 19.3－1， 在△ ABC 中， AB=AC，点D、 E 分别是线段 BC、 AD 的中点，过点 A 作 BC的平行线交 BE 的延长线于点 F，连接 CF．(1) 求证：△ BDE ≌△ FAE；(2) 求证：四边形 ADCF 为矩形．
解题秘方：本题考查了矩形的判定，全等三角形的判定和性质，等腰三角形的性质，正确地识别图形是解题的关键．
证明： (1)∵ AF ∥ BC，∴∠ AFE= ∠ DBE.∵ E 是线段 AD 的中点，∴ AE=DE，∵∠ AEF= ∠ DEB，∴△ BDE ≌△ FAE(AAS)；
(2)∵△ BDE ≌△ FAE，∴ AF=BD，∵ D 是线段 BC 的中点， ∴ BD=CD，∴ AF=CD，∵ AF ∥ CD，∴四边形 ADCF 是平行四边形，∵ AB=AC， D 是 BC 的中点，∴ AD ⊥ BC，∴∠ ADC=90°，∴平行四边形 ADCF 为矩形．
解法提醒由定义来判定矩形，要在平行四边形的基础上，证明有一个角是 90°，若在四边形的前提下，则需先证平行四边形，再证明有一个角是90°，矩形的定义既是矩形的性质也是矩形的判定 .
如图 19.3－2 所示，在矩形 ABCD 中，对角线 AC，BD 相交于点 O，∠ BOC=120°， AB=6.求：(1)对角线的长；(2) BC 的长；(3) 矩形 ABCD 的面积 .
解题秘方：紧扣矩形的“角、对角线的性质”进行计算 .
解： (1)∵四边形 ABCD 是矩形，∴ AC=BD， OA=OC=OB=OD.又∵∠ BOC=120°，∴∠ AOB=60°，∴△ AOB 是等边三角形，∴ OA=AB=6，∴ BD=AC=2OA=2×6=12.
解法提醒1. 有一个角是60°的等腰三角形是等边三角形.2. 矩形的两条对角线把矩形分成四个等腰三角形；另外，矩形的对角线与两邻边构成四个直角三角形，矩形中的有关计算通常需要用到等腰三角形或直角三角形的有关知识 .
直角三角形斜边上的中线的性质
特别提醒1. 直角三角形斜边上的中线把直角三角形分成两个面积相等的等腰三角形 .2. 此性质与“直角三角形中30°角所对的直角边等于斜边的一半”都是解决线段倍分关系的重要依据，但后者只在含30°角的直角三角形中才成立，而“直角三角形斜边上的中线等于斜边的一半”适用于所有直角三角形，更具一般性 .
说明： 直角三角形斜边上的中线等于斜边的一半，是根据矩形的两条对角线相等且互相平分推导出来的 . 将矩形沿某条对角线剪掉一半，剩下的一半就是直角三角形斜边上的中线等于斜边的一半的模型 .
[ 月考·成都 ] 如图 19.3 － 5，四边形 ABCD 中，∠ BAD=90°，∠ DCB=90°， E、 F 分别是 BD、 AC 的中点 .(1) 请你猜测 EF 与 AC 的位置关系，并给予证明；(2) 当 AC=8， BD=10 时，求 EF 的长 .
解题秘方：紧扣条件“E， F 分别为 BD， AC 的中点”，结合直角三角形斜边上中线的性质求解 .
技巧点拨1. 若题目中出现了一边的中点，往往需要用到中线，若又有直角，往往需要用到直角三角形斜边上的中线等于斜边的一半的性质.2. 在直角三角形中，遇到斜边的中点常作斜边上的中线，从而利用直角三角形斜边上的中线的性质把问题转化为等腰三角形的问题，利用等腰三角形的性质解决 .
1. 判定定理 1  对角线相等的平行四边形是矩形 .数学语言： 如图 19.3 － 7，在 ABCD 中，∵ AC=BD，∴四边形 ABCD 是矩形 .
2. 判定定理 2  三个角是直角的四边形是矩形 .数学语言： 如图 19.3 － 8，在四边形 ABCD 中，∵∠ A= ∠ B= ∠ C=90°，∴四边形 ABCD 是矩形 .
如图 19.3 － 9，在四边形 ABCD 中， AD ∥ BC， E，F 两点在边 BC 上， AB ∥ DE， AF ∥ DC，且四边形 AEFD 是平行四边形 .(1) AD 与 BC 有何数量关系？ 并说明理由 .(2)当 AB=DC 时，求证： ▱ AEFD 是矩形 .
解题秘方：紧扣“平行四边形”这一前提，从“对角线相等”入手(或有一直角入手)进行证明 .
解： BC=3AD. 理由如下：∵ AD ∥ BC， AB ∥ DE， AF ∥ DC，∴四边形 ABED 和四边形 AFCD 都是平行四边形，∴ AD=BE， AD=FC.又∵四边形 AEFD 是平行四边形，∴ AD=EF，∴ AD=BE=EF=FC，∴ BC=3AD.
(1) AD 与 BC 有何数量关系？ 并说明理由 .
证明： ∵四边形 ABED 和四边形 AFCD 都是平行四边形，∴ DE=AB， AF=DC.∵ AB=DC，∴ DE=AF.又∵四边形 AEFD 是平行四边形，∴四边形 AEFD 是矩形 .
(2)当 AB=DC 时，求证： AEFD 是矩形 .
方法点拨证明一个平行四边形为矩形的两种方法：一种是证明有一个角是直角，另一种是证明两条对角线相等 .本例采用的是对角线相等的方法.若采用有一个角是直角的方法，可证 DE=DC，结合EF=FC，利用等腰三角形“三线合一”可得∠ DFE=90° .
如图 19.3 － 10， ABCD 的四个内角的平分线分别相交于点 E， F， G， H.求证： 四边形 EFGH 是矩形 .
解题秘方：题中证明矩形是建立在四边形基础上的，且都与角相关，可从证直角入手进行判定 .
同理可得∠ AFB= ∠ AED=90°，∴∠ GFE= ∠ FEH= ∠ FGH=90°，∴四边形 EFGH 是矩形 .
思路点拨要判定一个四边形是矩形，通常选用“有三个角是直角的四边形是矩形”来证明；也可以先判定它是平行四边形，再根据平行四边形成为矩形应满足的条件，证明有一个角是直角或对角线相等即可.
直角三角形斜边上的中线性质