沪科版19.3 矩形 菱形 正方形一等奖ppt课件

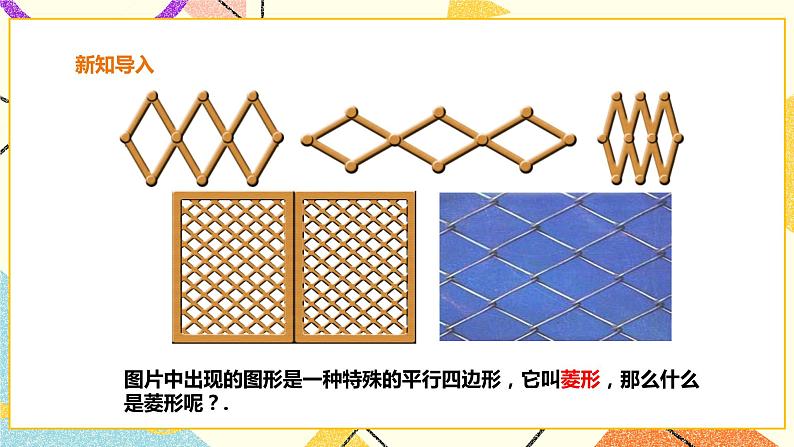
导入新课

师：同学们好，这节课我们继续学习新课，请观察下面图片，图片中框出的图形是你熟悉的吗？

师：图片中出现的图形是一种特殊的平行四边形，它叫菱形，那么什么是菱形呢？这节课让我们一起来学习吧.

认真观察，仔细思考，回顾，已学知识，回答问题，

 创设情景，导入新课，

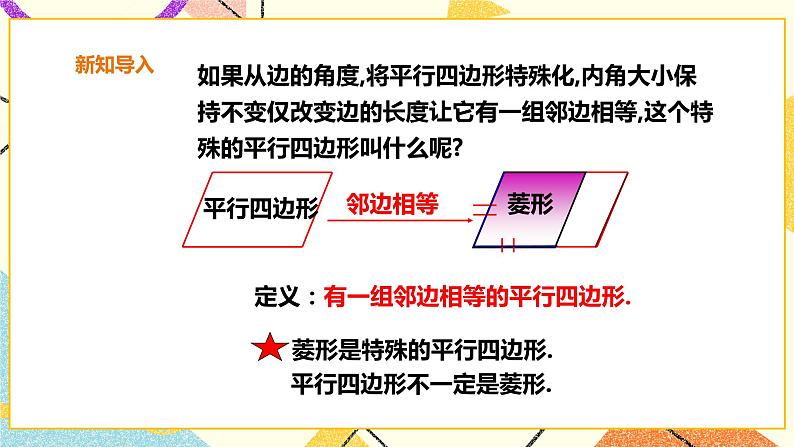
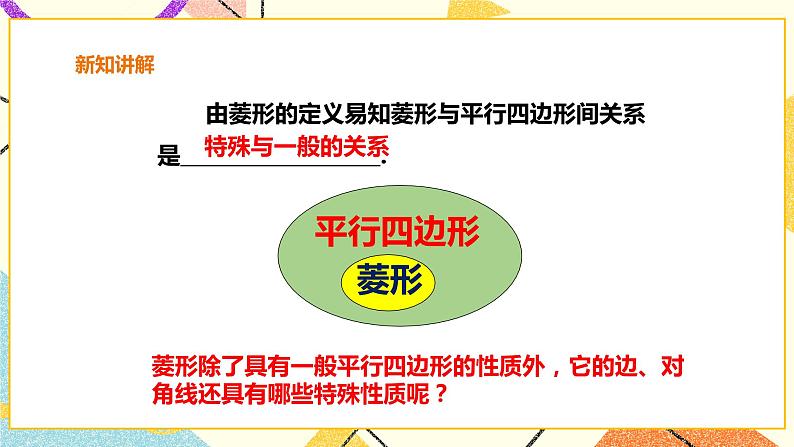
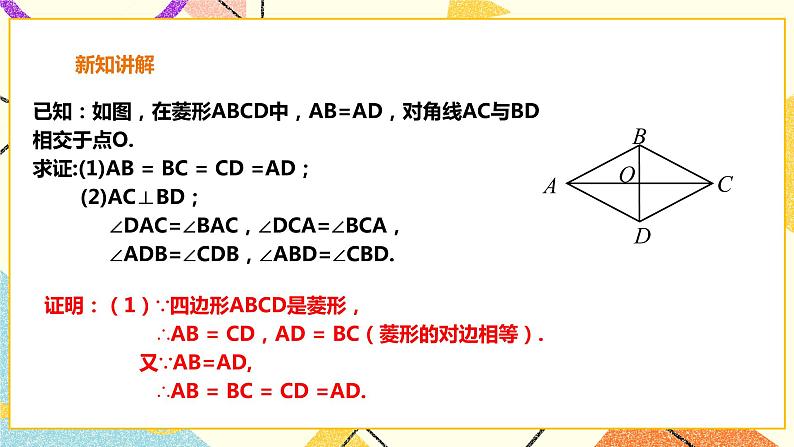
讲授新课

师：前面我们学习了平行四边形和矩形，知道了矩形是由平行四边形角的变化得到，如果平行四边形有一个角是直角时,就成为了矩形.

师：类比矩形,如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度让它有一组邻边相等,这个特殊的平行四边形叫什么呢?

1.菱形定义：有一组邻边相等的平行四边形

2. 概念辨析:平行四边形不一定是菱形

由菱形的定义易知菱形与平行四边形间关系是特殊与一般的关系. 但是不能说平行四边形不一定是菱形

师：同学们请思考一下，菱形除了具有一般平行四边形的性质外，它的边、对角线还具有哪些特殊性质呢？

师：将一张长方形的纸片按如图所示的方法进行对折、再对折，然后沿虚线剪下，打开后你知道它是什么图形吗？

问题1  菱形是轴对称图形吗?如果是,指出它的对称轴.

 是，两条对角线所在直线都是它的对称轴.

问题2  根据上面折叠过程，猜想菱形的四边在数量上有什么关系?菱形的两对角线有什么关系?

师：同学们可以猜想一下，

猜想1  菱形的四条边都相等.

猜想2  菱形的两条对角线互相垂直，并且每一条对角线平分一组对角.

师：下面我们来验证一下猜想，

已知：如图，在菱形ABCD中，AB=AD，对角线AC与BD相交于点O.     

求证:(1)AB = BC = CD =AD；

        (2)AC⊥BD；

       ∠DAC=∠BAC，∠DCA=∠BCA， 

       ∠ADB=∠CDB，∠ABD=∠CBD.

证明：（1）∵四边形ABCD是菱形，

        ∴AB = CD，AD = BC（菱形的对边相等）.

      又∵AB=AD,

       ∴AB = BC = CD =AD.

（2）∵AB = AD,

    ∴△ABD是等腰三角形.

     又∵四边形ABCD是菱形,

     ∴OB = OD （菱形的对角线互相平分）.

     在等腰三角形ABD中,

     ∵OB = OD，

     ∴AO⊥BD，AO平分∠BAD，

      即AC⊥BD，∠DAC=∠BAC.

      同理可证∠DCA=∠BCA， 

      ∠ADB=∠CDB，∠ABD=∠CBD.

小结：菱形是特殊的平行四边形，它除具有平行四边形的所有性质外，还有平行四边形所没有的特殊性质.

师：那么如何来判断一个四边形是菱形的？根据菱形的定义,可得菱形的第一个判定的方法：

∵四边形ABCD是平行四边形，

AB=AD，

∴四边形ABCD是菱形.

数学语言

有一组邻边相等的平行四边形叫做菱形.

师：请同学们思考一下，还有其他的判定方法吗？

猜想：四边都相等的四边形是菱形

师：下面是小刚同学的作图，分别以A、C为圆心,以大于 AC的长为半径作弧,两条 弧分别相交于点B , D,依次连接A、B、C、D四点.

师：想一想，根据小刚的作法你有什么猜想？你能验证小刚的作法对吗？

证明：∵AB=BC=CD=AD,

      ∴AB=CD , BC=AD.

      ∴四边形ABCD是平行四边形.

 又∵AB=BC,

   ∴四边形ABCD是菱形.

已知：如图，四边形ABCD中,AB=BC=CD=AD.

求证：四边形ABCD是菱形.

师：菱形的判定定理1：

四条边都相等的四边形是菱形

（邻边相等的平行四边形是菱形）

几何语言描述：

∵在四边形ABCD中，AB=BC=CD=AD，

∴四边形 ABCD是菱形.

师：那么从对角线上能不能判定菱形呢？

命题：对角线互相垂直的平行四边形是菱形.

证明：∵四边形ABCD是平行四边形

∴AO=CO

又∵ AC ⊥ BD;

∴DA=DC

∴  □ ABCD是菱形

师：由此我们可以得到，菱形的判定定理2：

对角线互相垂直的平行四边形是菱形；

（对角线互相垂直平分的四边形是菱形）

用几何语言可以表示为，

∵AC⊥BD，□ABCD

∴四边形ABCD是菱形

师：到此我们重新认识了菱形，并了解了菱形的性质及其判定方法，下面我们通过几道例题来看一下它的应用，

例1  已知菱形的两条对角线长分别为a，b， 求菱形的面积．

(1)用含a，b的代数式表示菱形ABCD的面积S；

(2)若a=6㎝，b=8㎝，求它的面积和周长．

例2   如图，□ABCD的两条对角线AC、BD相交于点O，AC=8，BD=6，AB=5.

求AD的长.

例3   如图，在△ABC中，∠B＝90°，AB＝6cm，BC＝8cm.将△ABC沿射线BC方向平移10cm，得到△DEF，A，B，C的对应点分别是D，E，F，连接AD.求证：四边形ACFD是菱形．

在老师的引导下，认真思考，积极探索菱形概念

积极思考，认真猜想，探索验证菱形的性质，

通过逆命题，探索菱形的判定方法，

在老师的引导下，初步应用所学的新知，

培养学生独立学习能力，探究能力，

培养学生猜想探索的能力，

培养学生逆向思维的能力，

巩固新知应用知识，

课堂练习

1．菱形的一条对角线长等于边长，则菱形的两邻角的度数是__________

2．菱形的边长是13cm，它的一条对角线BD=10cm, 对角线AC=        cm，菱形的面积是=            .

3.在四边形ABCD中，对角线AC，BD互相平分，若添加一个条件使得四边形ABCD是菱形，则这个条件可以是 （ ）                                              

 A．∠ABC=90° B．AC⊥BD

 C．AB=CD      D．AB∥CD

4.如图，将△ABC沿BC方向平移得到△DCE，连接AD，下列条件能够判定四边形ACED为菱形的是（　　）

  A．AB=BC     B．AC=BC   

  C．∠B=60°   D．∠ACB=60°

组内合作，独立探究，积极展示，

进一步巩固新知，

中考链接

1.(2018十堰) 菱形不具备的性质是（　　）

A．四条边都相等      B．对角线一定相等

C．是轴对称图形 　　 D．是中心对称图形

2.（2018舟山）用尺规在一个平行四边形内作菱形ABCD，下列作法中错误的是（  ）

积极思考，认真发言，

提升知识的应用能力，

课堂小结

今天你学到了什么

一个定义：

有一组邻边相等的平行四边形叫菱形

两个公式：

S菱形=底×高

S菱形= 对角线乘积的一半

三个特性：

特在“边、对角线、轴对称”

四个判定：

1、有一组邻边相等的平行四边形叫做菱形.

2、有四条边相等的四边形是菱形.

3、对角线互相垂直的平行四边形是菱形.

4、对角线互相垂直且平分的四边形是菱形.

梳理回顾所学知识，

培养学生的总结能力，

板书

一个定义：

有一组邻边相等的平行四边形叫菱形

两个公式：

S菱形=底×高

S菱形= 对角线乘积的一半

三个特性：

特在“边、对角线、轴对称”

四个判定：

1、有一组邻边相等的平行四边形叫做菱形.

2、有四条边相等的四边形是菱形.

3、对角线互相垂直的平行四边形是菱形.

4、对角线互相垂直且平分的四边形是菱形.

认真笔记，

为学生留下思维的线索，