沪科版七年级上册1.3 有理数的大小优质课课件ppt

这是一份沪科版七年级上册1.3 有理数的大小优质课课件ppt，共26页。PPT课件主要包含了在数轴上，记作│a│，叫做数a的绝对值，读作“a的绝对值”，绝对值的概念，绝对值的性质，知识回顾，要求一个数的绝对值，求出该数的绝对值，方法点拨等内容，欢迎下载使用。

表示数a的点与原点的距离
一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0.
(1)当a是正数时，｜a｜＝a ;(2)当a是负数时，｜a｜＝-a ;(3)当a是0时，｜a｜＝0.
三、求一个数的绝对值的方法：
首先判断这个数是正数、负数还是零，
然后根据“一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0”
注意：任何数都有绝对值，且只有1个.
① 互为相反数的两个数的绝对值相等.即 ｜a｜=｜-a｜
② 绝对值相等的两个数相等或互为相反数.
即若｜a｜=｜b｜,则 a=b 或 a=-b.
③ 绝对值等于一个正数的数有两个，它们互为相反数.
④ 几个非负数的和为0，则这几个数都为0.
① 同分子分数比较大小，分母大的分数反而小，分母小的分数反而大；
② 同分母分数比较大小，分子大的分数大，分子小的分数小；
③ 异分母分数比较大小，先通分，化成同分母分数，再比较大小.
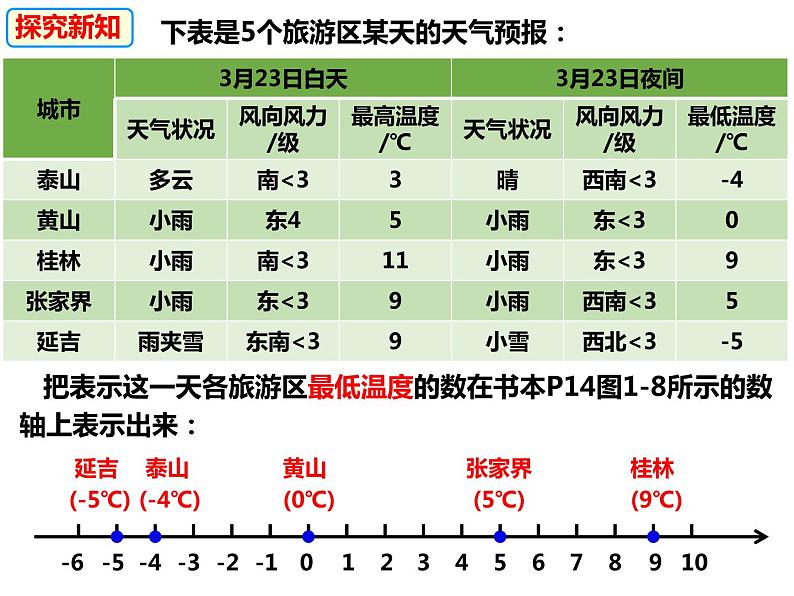
下表是5个旅游区某天的天气预报：
把表示这一天各旅游区最低温度的数在书本P14图1-8所示的数轴上表示出来：
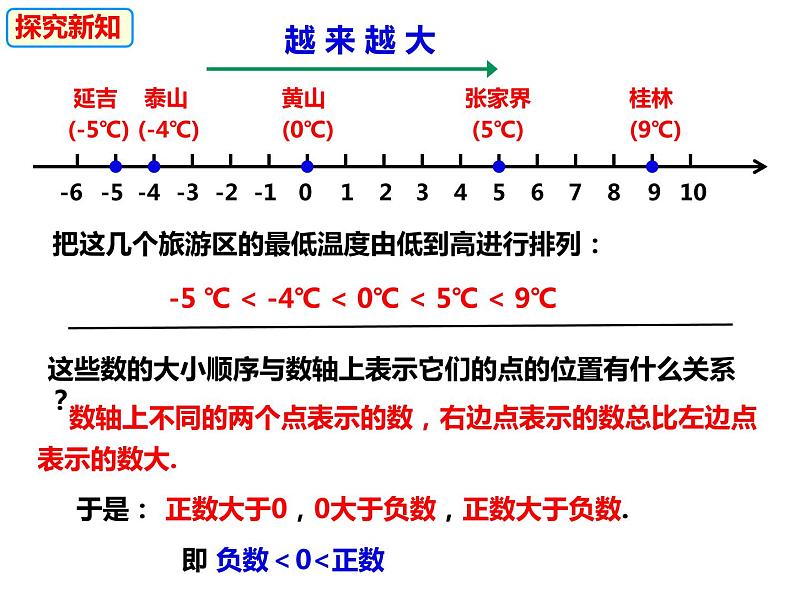
把这几个旅游区的最低温度由低到高进行排列：
-5 ℃ < -4℃ < 0℃ < 5℃ < 9℃
这些数的大小顺序与数轴上表示它们的点的位置有什么关系？
数轴上不同的两个点表示的数，右边点表示的数总比左边点表示的数大.
正数大于0，0大于负数，正数大于负数.
思考：如何比较 -3，0 , 2 的大小.
方法一：利用数轴比较有理数的大小 将各有理数在数轴上表示出来，再根据“ 数轴上不同的两个点表示的数，右边点表示的数总比左边点表示的数大”进行比较.
方法二：利用数的正负性比较大小 正数大于0，负数小于0，正数大于负数.即 负数＜0<正数
【思考】1、在数轴上分别表示下列各对数，比较它们的大小。 (1) -1 与 -1.5 (2) - 与 - (3) -2 与 -2.5 (4) -5 与 -0.5
(1) -1>-1.5
(3) -2>-2.5
(4) -5<-0.5
(2) - <-
【思考】2、求出上题中各对数的绝对值，并比较它们的大小.
【讨论】3、从上面的思考中，你发现了什么规律？
两个负数比较大小，绝对值大的反而小；
有理数大小的比较方法三：
利用绝对值比较两个负数的大小
(1) 只有比较两个负数的大小时，才能利用“绝对值比较法”；(2) 比较两个负数大小的一般步骤： 一求：分别求出两个负数的绝对值； 二比：比较两个绝对值的大小； 三判断：根据“绝对值大的反而小”进行判断．
两个负数比较大小，绝对值大的反而小.
例 比较下列每组数的大小：
(1) -2 和 -3
(2) - 和 -0.8
(1) 因为 |-2| = 2， |-3|= 3
(2) 因为 |- |=
所以 0.6 < 0.8
所以 - > -0.8
方法一：利用数轴比较有理数的大小 将各有理数在数轴上表示出来，再根据“ 数轴上不同的两个点表示的数，右边点表示的数总比左边点表示的数大”进行比较.方法二：利用数的正负性比较大小 正数大于0，负数小于0，正数大于负数.即 负数＜0<正数方法三：利用绝对值比较两个负数的大小 两个负数比较大小，绝对值大的反而小.
1、把下列各数在数轴上表示出来，并用“<”连接起来：
-3， ，-1，5，-2 ，0，2，+7
所以 -3<-2 <-1<0< <2<5<+7
在一个用不等式连接的式子中，若出现几个不等号，要么都用“>”,要么都用“<”,不能交替混用. 如不能出现如-1<0>-3的形式.
2、比较大小，要求写出比较过程.
(2) -(- ) 和 -│- │
【注意】带有括号或是绝对值的两个数进行大小比较，需先化简，再比较大小.最后的结果一定要是原来两数的大小关系.
(1) - 和 -
(5) -[-(- )] 和 -│- │
(3) - 和 -3.13
(3) -2 和 -
3、比较大小.(填“>”或“<”)：
(1) 6 -6;
(2) - -0.012;
(4) |-0.1| |-0.01|;
(4) -2 - ;
(5) -1 - ;
(6) -3.14 -π.
4、比较 -2 , - ，0.002 的大小关系是( )
A. 0.002 < - <-2
B. 0.002 < -2<-
C. - < -2 < 0.002
D. -2 < - < 0.002
7、大于 -1 而小于 2 的整数有 .
6、在 -0.1428 中用数字 3 代替其中一个非 0 数字后，使所得的数最大，则被替换的数字是( )
A.1 B.2 C.4 D.8
8、结合数轴，回答下列问题： (1) 有没有最大的正整数？有没有最小的正整数？如果有，是什么？ (2) 有没有最小的负整数？有没有最大的负整数？ 如果有，是什么？
解：(1) 没有最大的正整数，有最小的正整数是 1 . (2) 没有最小的负整数，有最大的负整数是 -1 .
9、已知 a，b，c，d 四个有理数，它们在数轴上的对应点的位置如图所示.
(1) 把 a，b，c，d 按从小到大的顺序排列；(2) 把 -a，-b，-c，-d 按从小到大的顺序排列；(3) 把│a│，│b│，│c│，│d│按从大到小的顺序排列.
解：(1) a(2) -a>-b>-c>-d
(3) │a│>│b│>│c│>│d│
10、有理数 a，b 在数轴上的对应点的位置如图所示，则 a，b，-a，│b│的大小关系正确的是 ( )
A. a>│b│>b>-a B.│b│>b>a>-aC.│b│>a>-a>b D. a>│b│>-a>b
11、已知有理数 a>0，b<0，c<0，且│c│>│b│>│a│,用“<”把 a，b，c，-a，-b，-c 连接起来.
12、将下面的直线补成一条数轴，并将下列各数在数轴上表示出来，并回答问题.
+5，-1 ，0，-2，
(1) 在数轴上表示+5和-2这两个点之间的距离是 ; (2) 将上面几个数用“<”连接起来； (3) 如果将表示 +5，0，-2 三个点分别用点 A，B，C 来表示，怎样移动点 A，B，C 中的两点，才能使三个点所表示的数相同(写出一种移动方法即可)？
高斯符号[x]首次出现在数学高斯的数学著作《算术研究》一书中，对于任意实数 x，通常用 [x] 表示不超过 x 的最大整数，如 [2.9]=2，给出如下结论： ① [-3]=-3 ② [-2.9]=-2 ③ [0.9]=0 ④[3.1]+[3.9]=9以上结论中，你认为正确的有 (填序号).