初中数学青岛版八年级下册11.1 图形的平移教课课件ppt

这是一份初中数学青岛版八年级下册11.1 图形的平移教课课件ppt，共19页。PPT课件主要包含了学习目标，知识回顾，巩固理解，典例剖析，随堂练习，巩固练习等内容，欢迎下载使用。

进一步掌握平移的概念与性质；
能够利用图形平移的特点与性质熟练解决相关问题.
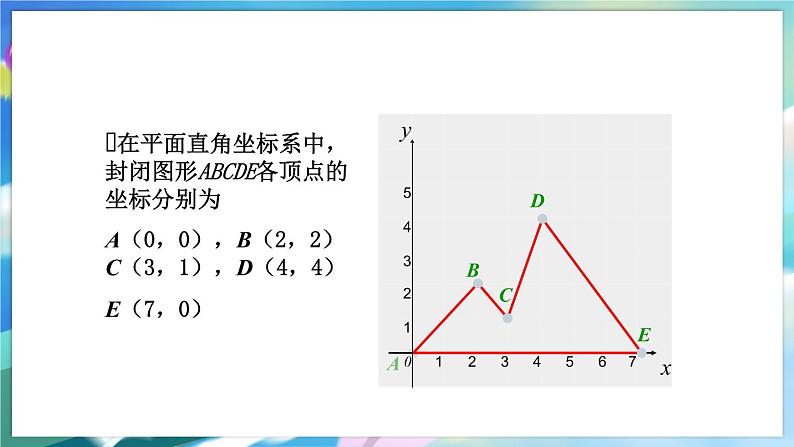
在平面直角坐标系中，封闭图形ABCDE各顶点的坐标分别为A（0，0），B（2，2）C（3，1），D（4，4）E（7，0）
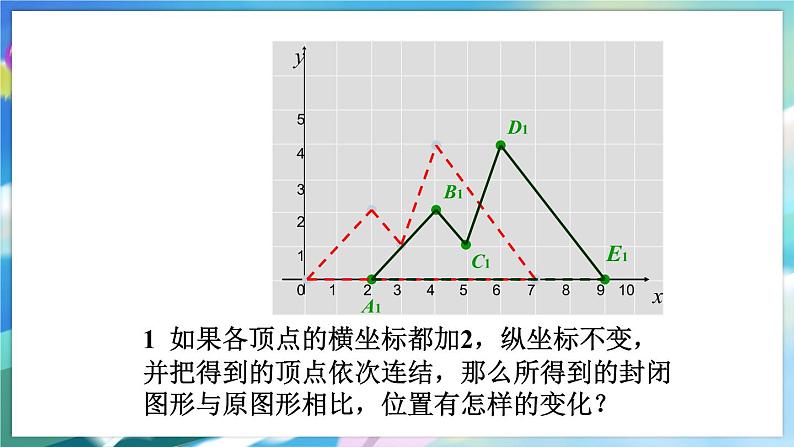
1 如果各顶点的横坐标都加2，纵坐标不变，并把得到的顶点依次连结，那么所得到的封闭图形与原图形相比，位置有怎样的变化？
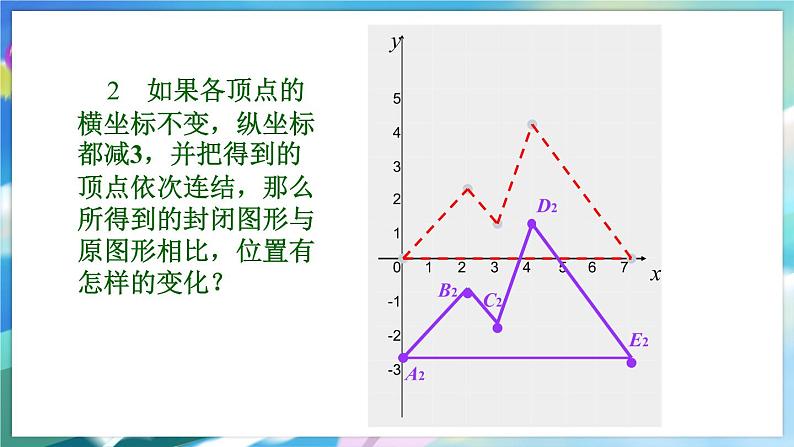
2 如果各顶点的横坐标不变，纵坐标都减3，并把得到的顶点依次连结，那么所得到的封闭图形与原图形相比，位置有怎样的变化？
平移只改变图形的位置，不改变图形的形状和大小.
在平面内，将一个图形沿某一个方向移动一定的距离，图形的这种变化叫做平移.
一个图形和它经过平移所得到的图形中，两组对应点的连线平行（或在同一条直线上）且相等.
1.如图所示，△DEF经过平移可以得到△ABC，那么平移后到达∠C位置的是（ ）A.∠EB.∠BODC.∠F D.∠BDO2.在平移过程中，平移前后的线段（ ）A.互相平行且相等 B.互相垂直且相等 C.互相平行(或在同一条直线上)且相等 D.在同一条直线上
3.如图，直角△ABC沿直角边BC所在的直线向右平移得到△DEF，下列结论中错误的是（ ） A.△ABC≌△DEF B.BE=CFC.AC=DF D.EC=CF
4.在上题中，若连接AD，则下列结论中错误的是（ ）A.四边形ADFC是平行四边形 B.四边形ADEB是矩形C.若AB=BE=3，则四边形ADEB是正方形 D.S四边形ADFC=EC·AB
5.如图，将等边△ABC沿射线BC向右平移到△DCE的位置，连接AD、BD，则下列结论：①AD=BC；②BD、AC互相平分；③四边形ACED是菱形．其中正确的个数是（ ） A．0 B．1 C．2 D．3
例2 如图，任意剪一张平行四边形纸片ABCD，设∠B＜90°.在边BC上取一点E，连接AE，沿AE将△ABE剪下，将它沿边AD向右平移，平移的距离等于AD的长.
解：（1）所得到的四边形AEFD是平行四边形.理由是：在上面的平移过程中，A与D，B与C，E与F分别是对应点，点B，E，C，F在同一条直线上，根据平移的基本性质，AD∥EF且AD=EF，所以四边形AEFD是平行四边形.
（1）试判断平移后所得到的四边形AEFD的形状，并说明理由；
（2） 由∠B＜90°，过点A作AE⊥BC，垂足为E，
点E在线段BC上、平移△ABE所得到的平行四边形AEFD是矩形（如图）.
（2）四边形AEFD能否是矩形？如果能，AE应满足什么条件？如果不能，请说明理由；
（3）四边形AEFD能否是菱形？如果能，AD应满足什么条件？如果不能，请说明理由.
当边AD等于对角线AC的长时，沿对角线将△ABC剪下，平移△ABE后所得到的平行四边形ACFD是菱形（如图）.
当AD大于AC或者AD小于点A到BC的距离时，对于边BC上的任意一点E，都不能使AE=AD， 平移△ABE后所得到的平行四边形，都不可能为菱形.
当AD小于AC，并且AD大于点A到BC的距离时，在边BC上截取点E，使AE=AD， 平移△ABE后所得到的平行四边形AEFD是菱形 (如下图）.
如图，△ABC中，∠B=90°，AB=6cm，BC=8cm，将△ABC沿射线BC方向平移10cm，得到△DEF，A，B，C的对应点分别是D，E，F，连接AD，求证：四边形ACFD是菱形.
1.△ABC从一个位置平移到另一个位置，则下列说法不正确的是（ ）A.AB=A′B′ B.AB//A′B′ C.四边形BCC′B′为平行四边形 D.AA′>BB′>CC′
2.如图，将面积为5的△ABC沿BC方向平移至△DEF的位置，平移的距离是边BC长的两倍，那么图中的四边形ACED的面积为多少？
如图，将平行四边形ABCD向左平移2个单位长度，可以得到平行四边形A1B2C3D4，画出平移后得图形，并指出各个顶点得坐标。