
湘教版九年级上册第3章 图形的相似3.4 相似三角形的判定与性质优质课件ppt
展开创设情境 新课导入
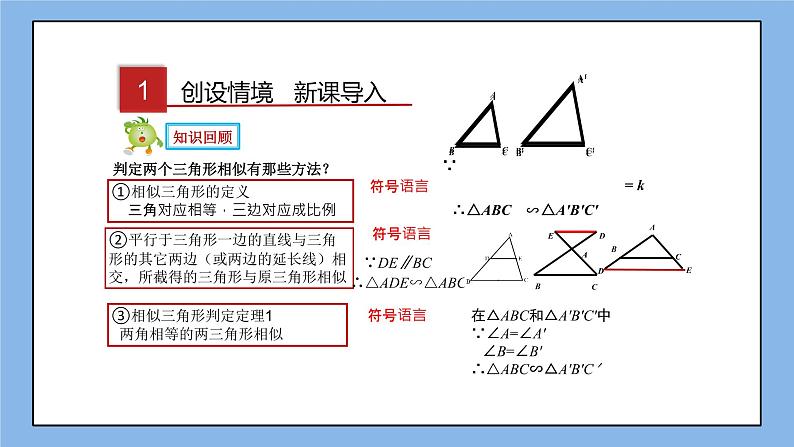
判定两个三角形相似有那些方法?
①相似三角形的定义 三角对应相等,三边对应成比例
②平行于三角形一边的直线与三角形的其它两边(或两边的延长线)相交,所截得的三角形与原三角形相似
③相似三角形判定定理1 两角相等的两三角形相似
在△ABC和△A′B′C′中∵∠A=∠A′ ∠B=∠B′ ∴△ABC∽△A′B′C′
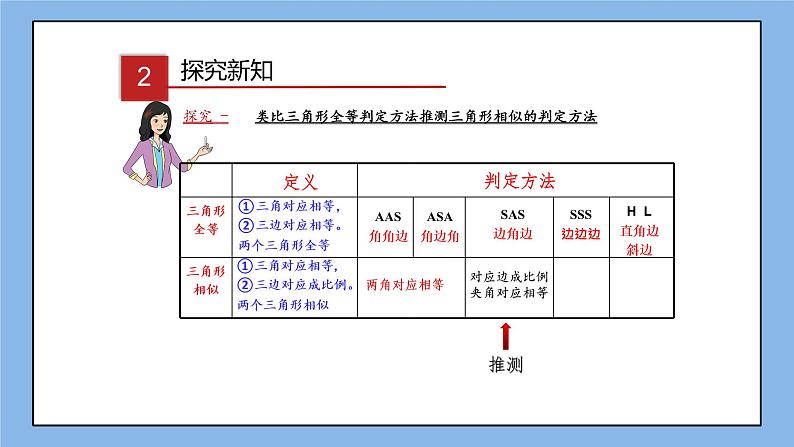
类比三角形全等判定方法推测三角形相似的判定方法
对应边成比例 夹角对应相等
①三角对应相等,②三边对应相等。两个三角形全等
①三角对应相等,②三边对应成比例。两个三角形相似
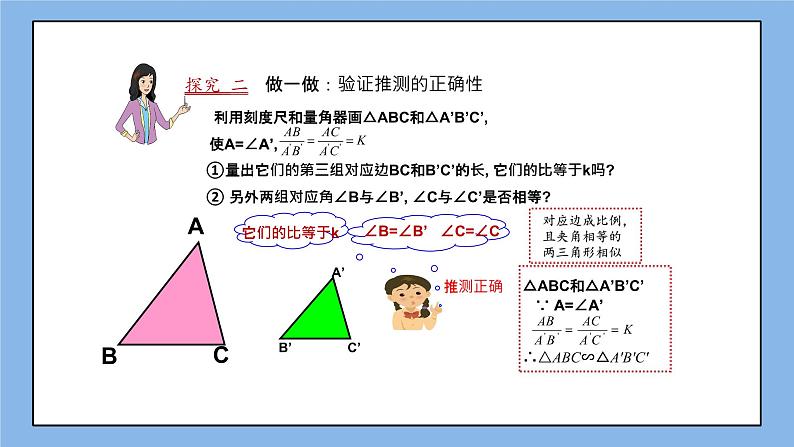
做一做:验证推测的正确性
对应边成比例, 且夹角相等的 两三角形相似
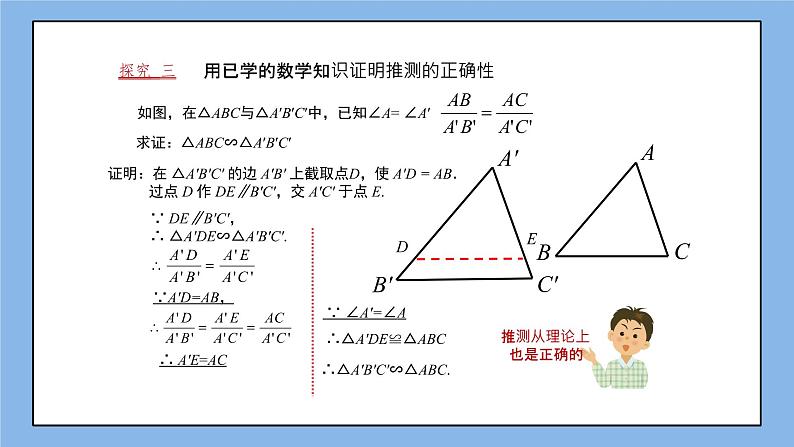
用已学的数学知识证明推测的正确性
求证:△ABC∽△A′B′C′
证明:在 △A′B′C′ 的边 A′B′ 上截取点D,使 A′D = AB. 过点 D 作 DE∥B′C′,交 A′C′ 于点 E.
∵ DE∥B′C′,∴ △A′DE∽△A′B′C′.
∴ A′E=AC
∴△A′DE≌△ABC
∴△A′B′C′∽△ABC.
推测从理论上 也是正确的
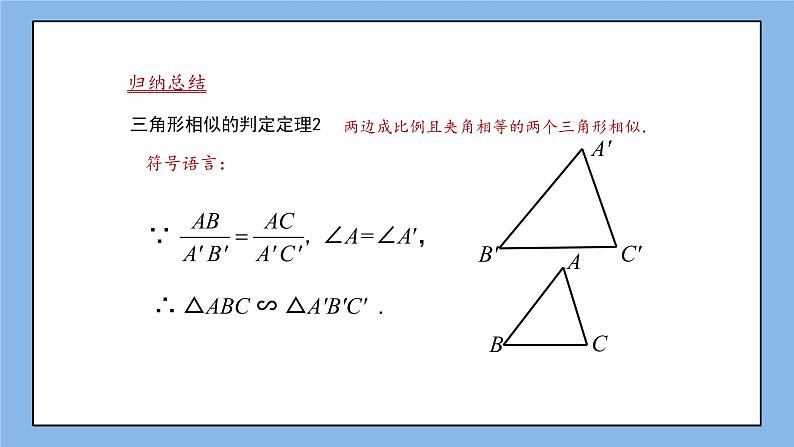
三角形相似的判定定理2
两边成比例且夹角相等的两个三角形相似.
∴ △ABC ∽ △A′B′C′ .
例1、在△ABC和△DEF中,∠C=∠F=70°,AC=3.5cm,BC=2.5 cm, DF=2.1 cm,EF=1.5 cm.求证:△DEF∽△ABC.
证明:∵AC=3.5cm,BC=2.5cm,DF=2.1cm,EF=1.5cm,
又∵∠C=∠F=70°,∴ △DEF∽△ABC(两边成比例且夹角相等的两个三角形相似)
方法总结:解题时要找准对应边.
解: ∵ CD是边AB上的高 ∴ ∠ADC= ∠CDB=90°
∴ △ADC∽△CDB∴ ∠ACD= ∠B∴ ∠ACB= ∠ACD+ ∠BCD= ∠B+ ∠BCD= 90°.
方法总结:解题时需注意隐含条件,如垂直关系,三角形的高等.
例3、如图所示,在△ABC中,D,E分别在AC,AB上且 , BC=6,则DE=( )
【类型一】利用相似三角形的判定定理2求值
∴△ADE∽△ABC.∵△ADE∽△ABC,∴
又∵BC=6,∴DE=3,故填3.
方法总结:此题考查相似三角形判定定理2的应用,首先根据已知条件证明两三角形相似,再利用相似得出相应结论求解.
例4、如图所示,已知四边形ABCD的对角线AC与BD相交于点O,且OA=1,OB=1.5,OC=3,OD=2,求证:△OAD∽△OBC.
【类型二】利用相似三角形的判定定理2证明相似
且∠AOD=∠BOC,
∴根据相似三角形的判定定理2得△OAD∽△OBC,即证.
方法总结:解答此类问题应先找成比例线段,再利用判定定理2证三角形相似.
解析:已有对顶角相等,再证两边对应成比例,即可得△OAD∽△OBC.
如图:在△ABC中,D﹑E分别在AB﹑AC上,请你加一个条件使△ADE∽△ABC,这个条件可以是_______
相似三角形的判定定理2
内容:两边对应成比例,且夹角相等的两个三角形相似
相似三角形判定定理2的运用
湘教版九年级上册第3章 图形的相似3.4 相似三角形的判定与性质获奖ppt课件: 这是一份湘教版九年级上册第3章 图形的相似3.4 相似三角形的判定与性质获奖ppt课件,共17页。PPT课件主要包含了什么叫相似三角形,复习导入,∠A∠A,探究新知,已知∠A∠A,∵DE∥BC,又ADAB,∴AEAC,∵∠A∠A,∴∠ACD∠B等内容,欢迎下载使用。
数学湘教版3.4 相似三角形的判定与性质精品课件ppt: 这是一份数学湘教版3.4 相似三角形的判定与性质精品课件ppt,共14页。PPT课件主要包含了激趣导入,探究新知,∴∠DHE∠A,∴EF24,△ABE∽△FCE,△FCE∽△FDA,△ABE∽△FDA,课后作业,∴∠A∠ECD,课堂小结等内容,欢迎下载使用。
数学湘教版3.4 相似三角形的判定与性质优质教学ppt课件: 这是一份数学湘教版3.4 相似三角形的判定与性质优质教学ppt课件,文件包含教学课件九上·湘教·341相似三角形的判定第3课时相似三角形的判定定理2pptx、数学九上·湘教·341相似三角形的判定第3课时相似三角形的判定定理2教案docx等2份课件配套教学资源,其中PPT共14页, 欢迎下载使用。













