

湘教版九年级上册3.4 相似三角形的判定与性质完美版ppt课件
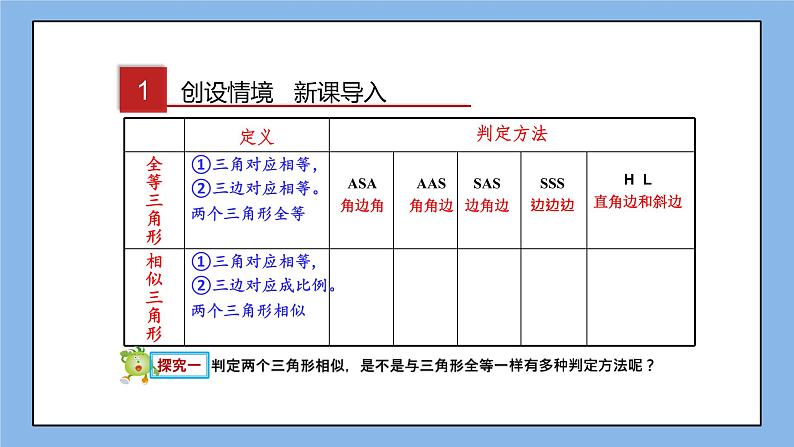
展开创设情境 新课导入
判定两个三角形相似,是不是与三角形全等一样有多种判定方法呢?
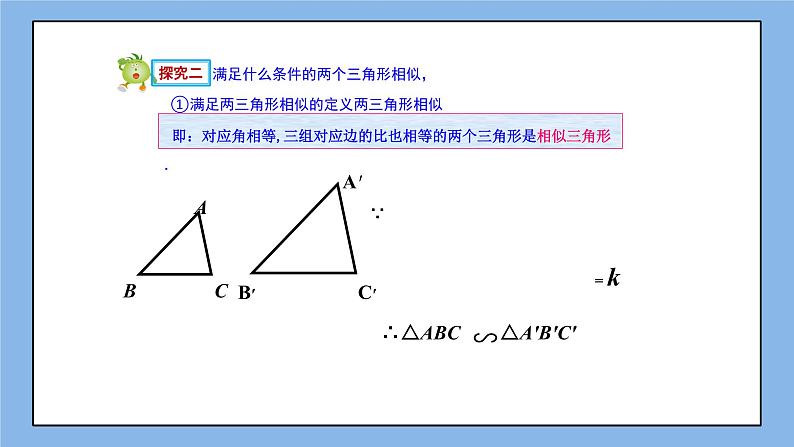
满足什么条件的两个三角形相似,
①满足两三角形相似的定义两三角形相似
即:对应角相等,三组对应边的比也相等的两个三角形是相似三角形.
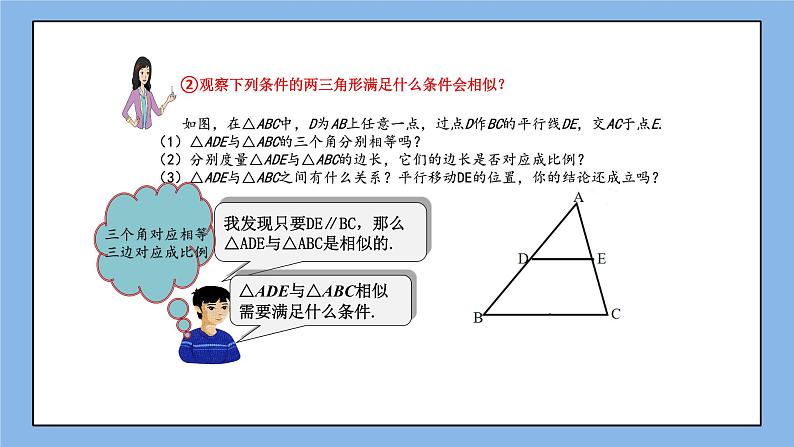
②观察下列条件的两三角形满足什么条件会相似?
如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.(1)△ADE与△ABC的三个角分别相等吗?(2)分别度量△ADE与△ABC的边长,它们的边长是否对应成比例?(3)△ADE与△ABC之间有什么关系?平行移动DE的位置,你的结论还成立吗?
我发现只要DE∥BC,那么△ADE与△ABC是相似的.
△ADE与△ABC相似需要满足什么条件.
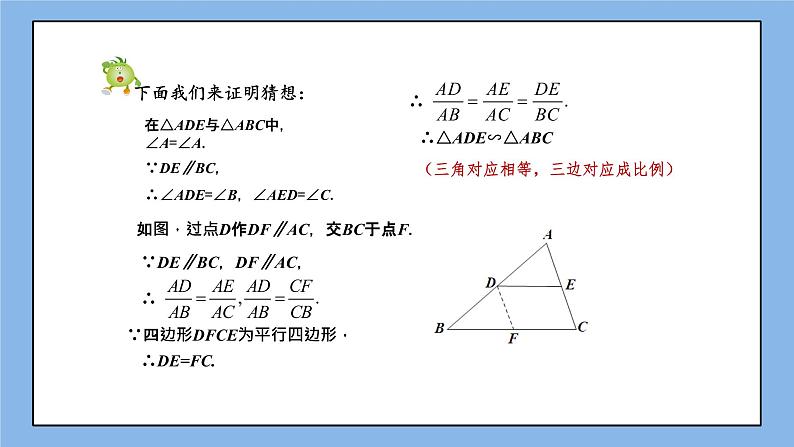
在△ADE与△ABC中,∠A=∠A.∵DE∥BC,∴∠ADE=∠B,∠AED=∠C.
∵DE∥BC,DF∥AC,
如图,过点D作DF∥AC,交BC于点F.
∵四边形DFCE为平行四边形,
(三角对应相等,三边对应成比例)
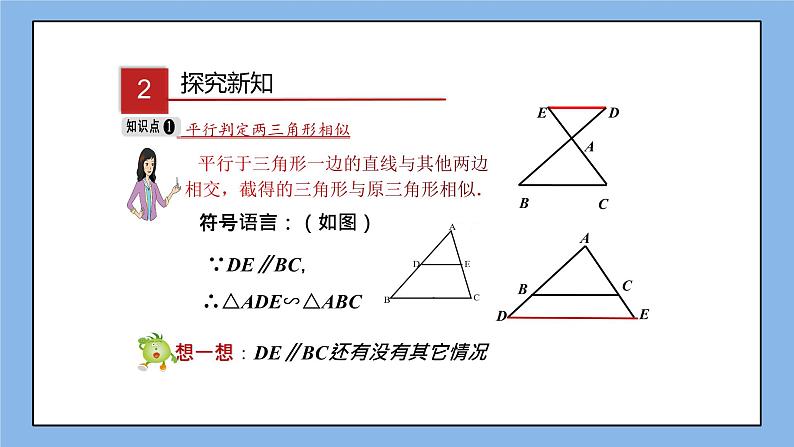
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
平行判定两三角形相似
想一想:DE∥BC还有没有其它情况
例1:在△ABC中,已知点D,E分别是AB,AC边的中点.求证: △ ADE∽△ ABC.
证明 ∵点D,E分别是AB,AC边的中点,
例2 如图,点D为△ABC的边AB的中点,过点D作DE∥BC,交边AC于点E.延长DE至点F,使DE=EF. 求证:△CFE∽△ABC.
证明 ∵DE∥BC,点D为△ABC 的边AB的中点,
又DE=FE,∠AED=∠CEF,
∴△ADE≌△CEF.
∴△ADE∽△ABC.
∴△CFE∽△ABC.
【类型一】利用平行线判定三角形相似
例3、如图所示,DE∥FG∥BC,图中相似三角形共有( )
解析:△ADE∽△AFG,△ADE∽△ABC, △AFG∽△ABC,故选B. 方法总结:本题考查平行判定三角形相似的方法,解题时要考虑到所有情况,避免错解.
A.4对 B.3对 C.2对 D.1对
例4、如图,EF在平行四边形ABCD的边AB的延长线上,且EF=AB,DE交CB于点M.求证:△BME∽△BCF.
解析:要证△BMF∽△BCF,可先证ME∥CF.证明:∵四边形ABCD为平行四边形,∴AB∥CD,AB=CD.又∵EF在AB的延长线上,且EF=AB,∴EF∥CD,EF=CD.即四边形CDEF为平行四边形,∴ME∥CF,∴△BME∽△BCF.
方法总结:本题考查利用平行判定三角形相似的基本运用,与平行四边形的性质相结合,解题时要注意利用平行关系进行转化.
【类型二】利用平行线判定三角形相似求值
例5、如图,DE∥BC交AB于点D,交AC于E,若AD∶DB=3∶5,求DE∶BC的值.解析:由DE∥BC得△ADE∽△ABC,进而推出对应边成比例.解:∵DE∥BC,∴△ADE∽△ABC,∴∵∴ ∴ 方法总结:利用平行判断三角形相似,平行线分线段成比例,相似三角形性质,是求线段比值基本思路之一.
例6、如图,在▱ABCD中,E在AB上,CE,BD交于F,若AE∶BE=4∶3,且BF=2,则DF=____.
利用平行判定三角形相似方法
内容:平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
数学3.4 相似三角形的判定与性质优质课课件ppt: 这是一份数学3.4 相似三角形的判定与性质优质课课件ppt,共14页。PPT课件主要包含了情境导入,探究新知,∵DE∥BC,又A′DAB,由勾股定理得,1SAS相似,2AA相似,3SSS相似,课后练习,∴AC4等内容,欢迎下载使用。
数学湘教版3.4 相似三角形的判定与性质精品课件ppt: 这是一份数学湘教版3.4 相似三角形的判定与性质精品课件ppt,共14页。PPT课件主要包含了激趣导入,探究新知,∴∠DHE∠A,∴EF24,△ABE∽△FCE,△FCE∽△FDA,△ABE∽△FDA,课后作业,∴∠A∠ECD,课堂小结等内容,欢迎下载使用。
九年级上册3.4 相似三角形的判定与性质一等奖ppt课件: 这是一份九年级上册3.4 相似三角形的判定与性质一等奖ppt课件,共13页。PPT课件主要包含了SAS,ASA,AAS,SSS,复习导入,探究新知,∵DE∥BC,∴DEFC,∴DE∥BC,∴AECE等内容,欢迎下载使用。













