初中数学湘教版九年级上册2.3 一元二次方程根的判别式精品课件ppt

这是一份初中数学湘教版九年级上册2.3 一元二次方程根的判别式精品课件ppt，共13页。PPT课件主要包含了探究新知，针对训练，想一想，思考题等内容，欢迎下载使用。

创设情境 新课导入
1.变形: 化已知方程为一般形式; 2.确定系数:用a,b,c写出各项系数;3.计算、判断: b2-4ac的值; 若b2-4ac ≥0，则利用求根公式求出; 若b2-4ac<0，则方程没有实数根.4.代入:把有关数值代入公式计算;5.定根:写出原方程的根.
回顾一下用公式法解一元二次方程步骤
第三步中为什么要对 再代入求根公式求解？

此时，原方程有两个相等的实数根.
由于0的平方根为0，所以原方程的根为
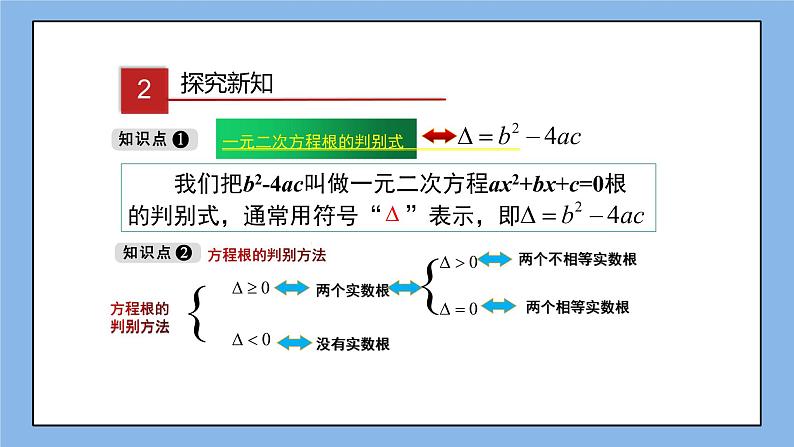
一元二次方程根的判别式
方程根的判别方法
例如1:不解方程，判断下列方程的根的情况．（1）3x2+4x－3=0； （2）4x2=12x－9; (3) 7y=5(y2+1).
解：（1）3x2+4x－3=0， ∵a=3,b=4,c=－3, ∴∆=b2－4ac =32－4×3×(-3) =52＞0.∴方程有两个不相等的实数根．
解：2）方程化为： 4x2－12x+9=0, ∵a=4,b=-12,c=9, ∴∆=b2－4ac =(－12)2－4×4×9=0. ∴方程有两个相等的实数根．
解：（3）方程化为： 5y2－7y+5=0, ∵a=5,b=－7,c=5, ∴∆=b2－4ac =(－7)2－4×5×5 =－51＜0.∴方程有两个相等的实数根．
3.判别根的情况，得出结论.
1.化为一般式，确定a,b,c的值.
2.计算∆的值，确定∆的符号.
一元二次方程根的判别式的应用一：不解方程判断方程根的情况
例如2:不解方程，判别关于x的方程 的根的情况.
一元二次方程根的判别式的应用二： 根据方程根的情况确定字母的取值范围
例4.关于x的一元二次方程 有两个实根，则m的取值范围是 .
例5:若关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根， 则k的取值范围是 ( ) A.k>-1 B.k>-1且k≠0 C.k<1 D.k<1且k≠0
解析：由方程有两个不相等的实数根，则b2-4ac>0， 由是关于x的一元二次方程，则二次项系数不为0，即k≠0解：由题意，得 故选B.
在等腰△ABC 中，三边分别为a,b,c，其中a=5，若关于x的方程x2+(b+2)x+6-b=0有两个相等的实数根，求△ABC 的周长.