鲁教版 (五四制)九年级上册2 二次函数公开课课件ppt

3.3 二次函数y=ax2的图象与性质（2）

教材分析

本节课要研究的问题是关于函数y=ax2的图象的作法和性质，逐步积累研究函数图象和性质的经验．

“刹车距离”是二次函数关系的应用之一，本节借助晴天和雨天刹车距离的不同，引出二次函数y＝ax2的系数a对图象的影响．由此可知二次函数是某些实际问题的数学模型．

由现实生活中的“刹车距离”联系到二次函数，说明数学应用的广泛性及实用性。

在教学中，由实际问题入手，能激起学生的学习兴趣和信心，运用类比的学习方法，通过与y=x2的图象和性质的比较，总结出它们的异同，从而更进一步地掌握不同形式的二次函数的图象和性质．

教学目标

(一)教学知识点

1．能作出y=ax2的图象．并研究它们的性质．

2．比较y=ax2与y=x2的异同．理解a对二次函数图象的影响．

(二)能力训练要求

1．经历探索二次函数y=ax2的图象的作法和性质的过程，进一步获得将表格、表达式、图象三者联系起来的经验．

2．通过比较y＝ax2与y=x2的图象和性质的比较．培养学生的比较、鉴别能力．

(三)情感与价值观要求

1．由“刹车距离”与二次函数的关系．体会二次函数是某些实际问题的数学模型．

2．由有趣的实际问题，使学生能积极参与数学学习活动，对数学有好奇心和求知欲．

教学重点

1．能作出y＝ax2的图象，并能够比较它们与y＝x2的异同，理解a对二次函数图象的影响．

2．能说出y＝ax2图象的开口方向；对称轴和顶点坐标．

教学难点

能作出函数y＝ax2的图象，并总结其性质，还能和y=x2作比较，

教学方法

类比学习法．

教具准备

投影片三张

第一张：(记作§3．3．2 A)

第二张：(记作§3．3．2 B)

第三张：(记作§3．3．2 C)

教学过程

Ⅰ．创设问题情境，引入新课

[师]在前两节课我们学习了二次函数的定义，会画函数y＝x2与y=－x2的图象，知道它们的图象是抛物线，并且还研究了抛物线的有关性质．与图象x轴是否有交点，交点坐标是什么?y随x的增大而如何变化．抛物线是否为轴对称图形等．

那么二次函数是否只有y＝x2与y＝－x2这两种呢?本节课我们继续学习其他形式的二次函数．

Ⅱ．新课讲解

一、刹车距离与二次函数的关系．

[师]大家知道两辆车在行驶时为什么要保持一定距离吗?

[生]怕发生“迫尾”事故．

[师]汽车刹车时向前滑行的离与什么因素有关呢?

[生]与汽车行驶的速度有关系．

[师]究竟与什么有关，关系有多大呢?

投影片：(§3．3．2 A)

影响刹车距离的最主要因素是汽车行驶的速度及路面的摩擦系数．有研究表明，晴天在某段公路上行驶时，速度为v(km／h)的汽车的刹车距离s(m)可以由公式s＝v2确定，雨天行驶时，这一公式为s＝v2．

[师]引刹车距离s与速度v之间的关系是二次函数吗?

[生]根据二次函数的定义可知，它们都是二次函数．

[师]与一上节课中学习的二次函数y＝x2和y＝－x2有什么不同吗?

[生]y＝x2中的a为1．

s＝ v2中的a为.

所以它们的不同之处在于a的取值不同．

[师]很好．

既然s＝v2和s=v2与y=x2,y=－x2它都是二次函数，且都是只含二次项的二次函数，所以它们有相同之处；又因为它们中的a值的不同．所以它们肯定还有不同之处．比如在y＝x2中自变量x可以取正数或负数，在s＝v2中，因为v是速度，能否取负值呢?由实际情况可知”不可以取负值．

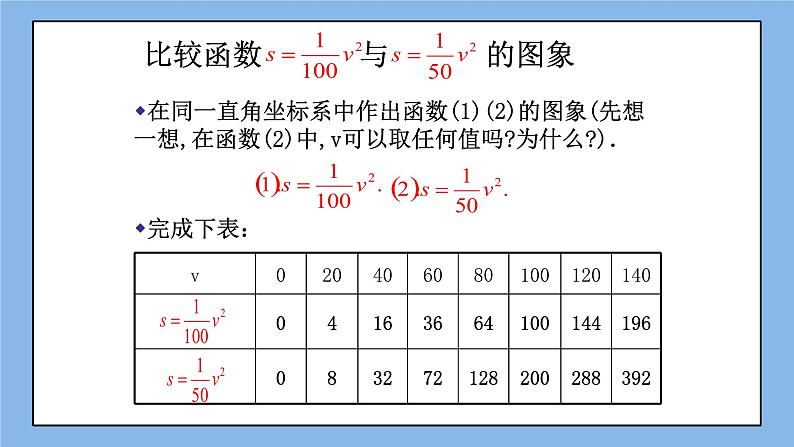
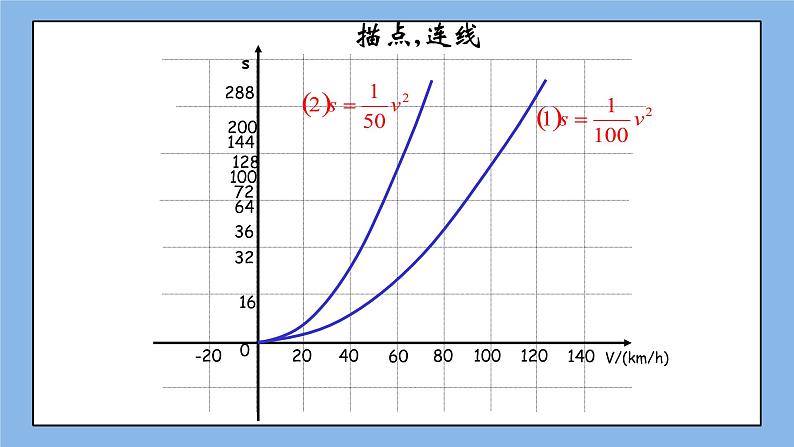
下图是s＝v2的图象，根据画图象的三个步骤即列表、描点、连线，在同一直角坐标系内作出函数s=v2的图象．

二、比较s= v2和s＝v2的图象．

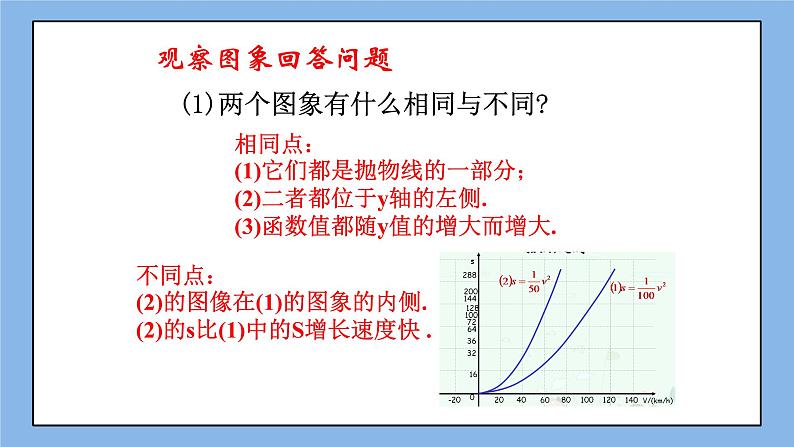
[师]从上图中，大家可以互相讨论图象有什么相同与不同?

[生]相同点：

(1)它们都是抛物线的一部分

(2)二者都位于s轴的左侧．

(3)函数值都随v值的增大而增大．

不同点：

(1)s=v2的图象在s= v2的图象的内侧．

(2)s= v2的s比s＝ v2中的S增长速度快．

[师]如果行车速度是60 km／h，那么在雨天行驶和在晴天行驶相比，刹车距离相差多少米?

[生]已知v＝60 km／h．分别代入s＝v2与s＝v2中．相应地求出各自的刹车距离，再求它们的差，即s1＝ × 602=72，

s2=×602＝36．则

s1－s2＝72－36＝36(m)．

所以在雨天行驶和在晴天行驶相比，雨天的刹车距离较长，相差36 m．

三、做一做

投影片：(§3．3．2 B)

作二次函数y＝2x2的图象．

(1)完成下表：

(2)在下图中作 出y＝2x2的图象．

(3)二次函数y＝2x2的图象是什么形状?它与二次函数y=x2的图象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?

[生](1)略  (2)如图

(3)二次函数y=2x2的图象是抛物线．

它与二次函数y＝x2的图象的相同点：

开口方向相同，都向上．

对称轴都是y轴．

顶点都是原点，坐标为(0，0)．

在y轴左侧，都是y值随x值的增大而减小；在y轴右侧，都是y值随x值的增大而增大．

都有最低点，即原点．

函数都有最小值．

不同点：y＝2x2的图象在y＝x2的图象的内侧．

y＝2x2中函数值的增长速度较快．

四、议一议

投影片：(§3．3．2C)

(1)在同一直角坐标系内作出函数y＝－2x2与y＝－x2的图象．并比较它们的性质．

(2)由上可得出什么?

[生](1)图象如下：

比较性质如下：

相同点：

开口向下，对称轴是 y 轴，顶点坐标是原点．

不同点：

开口程度不同，x2 的系数越大，抛物线的开口越大．

(2)总结：

函数y=ax2(a≠0)的图象和性质

一般地，抛物线 y=ax2 的对称轴是 y轴，顶点是原点．当a>0时，抛物线的开口向上，顶点是抛物线的最低点，a 越大抛物线开口越小；当a<0时，抛物线的开口向下，顶点是抛物线的最高点，a 越大抛物线开口越大．

|a|越大,开口越小．

Ⅲ．课堂练习

画出函数y＝x2与y＝2x2的图象．(在同一直角坐标系内)并比较它们的性质．

分析：画函数图象的步骤有列表、描点、连线．

解：

分别描点画图．

相同点：图象都是抛物线，开口方向相同、顶点相同，都有最低点，函数有最小值．y的值随x的增大而变化情况相同．

不同点：抛物线的开口大小不同，函数值的增长速度不同．

Ⅳ．课时小结

本节课巩固了画函数图象的步骤：列表、描点、连线；学习了刹车距离与二次函数的关系；并比较了函数y＝2x2与y=x2，y＝－2x2与y＝－x2的图象的性质．

Ⅴ．课后作业

习题3.5

板书设计

3.3 二次函数y=ax2的图象与性质（2）

一、1. 刹车距离与二次函数的关系(投影片§3．3．2 A)

2．比较s＝v2与s＝v2的图象

3．做一做(投影片§3．3．2 B)

4．议一议(投影片§3．3．2 C)

二、课堂练习

三、课时小结

四、课后作业

备课资料

参考练习

1．在同一直角坐标系内画出下列函数的图象：

(1)y＝3x2  (2)y＝－3x2  (3)y＝x2

答案：略

2．分别说出抛物线y=4x2与y=－x2的开口方向、对称轴与顶点坐标．

答案：y＝4x2的开口方向向上，对称轴为y轴．顶点坐标为(0，0)．

3．函数y＝5x2的图象在对称轴哪侧?y随着x的增大怎样变化?

答案：函数y＝5x2的图象在对称轴右侧部分．y随着x的增大而增大．

4．函数y＝－5x2有最大值或最小值吗?如果有，是最大值还是最小值?这个值是多少：

答案：函数y＝－5x2有最大值，这个值是0．