北京课改版九年级上册21.3 圆的对称性课文ppt课件

这是一份北京课改版九年级上册21.3 圆的对称性课文ppt课件，

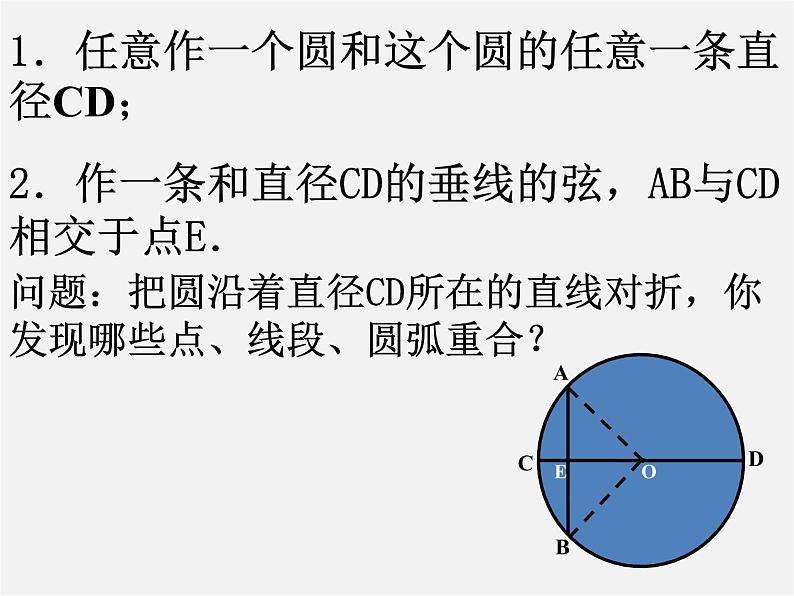
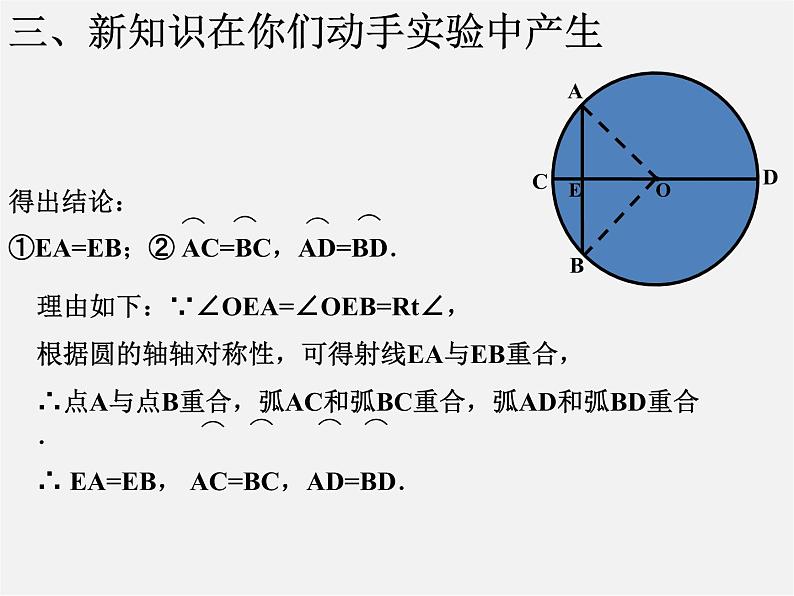
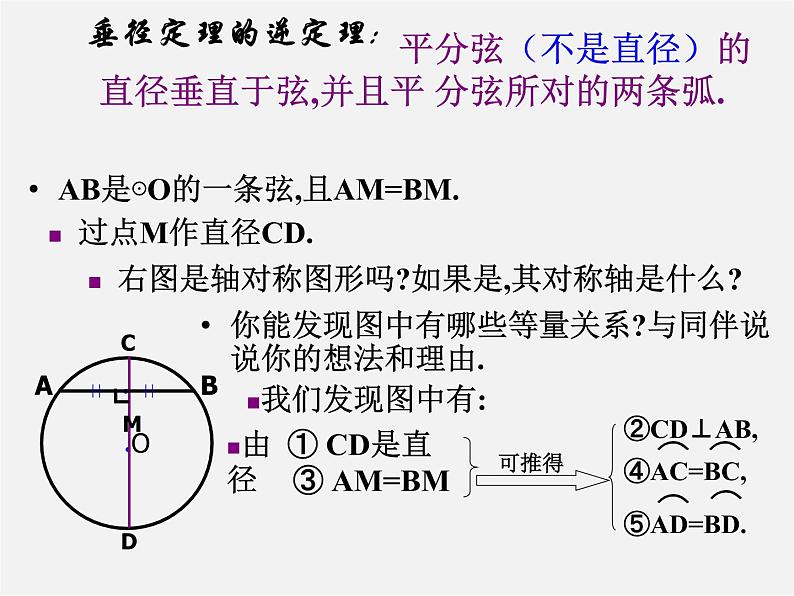
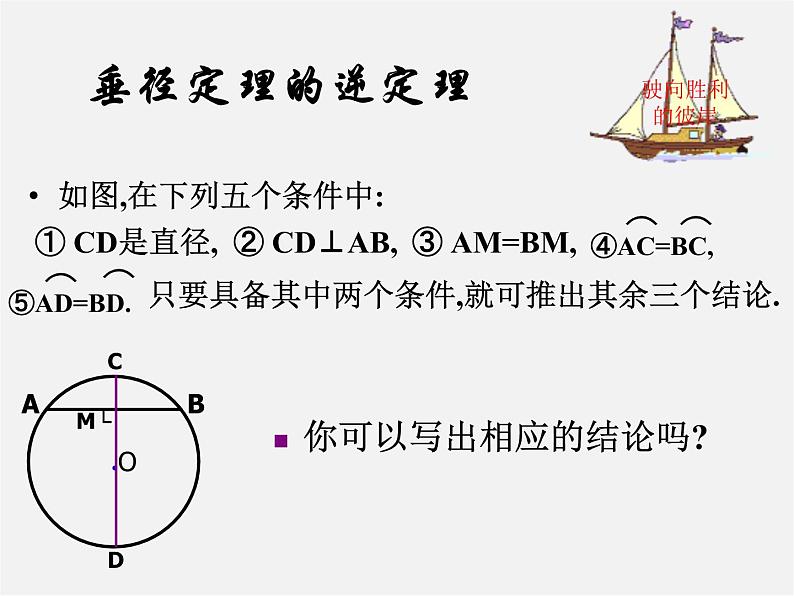
22.3圆的对称性（一）轴对称1．若将一等腰三角形沿着底边上的高对折， 将会发生什么结果?２．如果以这个等腰三角形的顶点为圆心，腰长为半径作圆，得到的圆是否是轴对称图形呢？二、新课1．结论：圆是轴对称图形，它有无数条对称轴，经过圆心每一条直线都是它的对称轴．强调：（1）对称轴是直线，不能说每一条直径都是它的对称轴；（2）圆的对称轴有无数条．判断：任意一条直径都是圆的对称轴（ ）1．任意作一个圆和这个圆的任意一条直径CD；2．作一条和直径CD的垂线的弦，AB与CD相交于点E．问题：把圆沿着直径CD所在的直线对折，你发现哪些点、线段、圆弧重合？三、新知识在你们动手实验中产生归纳得出：垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧．垂径定理的几何语言②CD⊥AB,垂径定理的逆定理:AB是⊙O的一条弦,且AM=BM.你能发现图中有哪些等量关系?与同伴说说你的想法和理由.过点M作直径CD.右图是轴对称图形吗?如果是,其对称轴是什么?我们发现图中有:由 ① CD是直径③ AM=BM┗ 平分弦（不是直径）的直径垂直于弦,并且平 分弦所对的两条弧.你可以写出相应的结论吗?垂径定理的逆定理如图,在下列五个条件中:只要具备其中两个条件,就可推出其余三个结论.① CD是直径,③ AM=BM,② CD⊥AB,观察下列哪些图形满足“垂直于弦的直径”的条件？为什么？ BADCOABDOABDOABCDO图5ABCDO图6OABCD图7图8图9图10ＥＥＥＥＥ例1 如图，两个圆都以点O为圆心，小圆的弦CD与大圆的弦AB在同一条直线上。你认为AC与BD的大小有什么关系？为什么？例2 一条排水管的截面如图所示．排水管的半径OB=10，水面宽AB=16，求截面圆心O到水面的距离OC ．思路：例3 已知：如图，线段AB与⊙O交于C、D两点，且OA=OB ．求证：AC=BD ．思路：作OM⊥AB，垂足为M ∴CM=DM ∵OA=OB ∴AM=BM ∴AC=BD．圆心到圆的一条弦的距离叫做弦心距．小结：1．画弦心距是圆中常见的辅助线；2 ．半径（r)、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路，它们之间的关系：1．已知⊙0的半径为13，一条弦的AB的弦心距为5，则这条弦的弦长等于 ． 24C五、目标训练4．如图，⊙O的直径为10，弦AB长为8，M是弦AB上的动点，则OM的长的取值范围是（ ） A．3≤OM≤5 B．4≤OM≤5 C．3

相关课件

数学九年级上册第二十一章 圆（上）21.2 过三点的圆集体备课课件ppt： 这是一份数学九年级上册第二十一章 圆（上）21.2 过三点的圆集体备课课件ppt，

初中数学北京课改版九年级上册21.3 圆的对称性集体备课ppt课件： 这是一份初中数学北京课改版九年级上册21.3 圆的对称性集体备课ppt课件，

初中数学北京课改版九年级上册21.2 过三点的圆课文内容课件ppt： 这是一份初中数学北京课改版九年级上册21.2 过三点的圆课文内容课件ppt，